Зарождение геометрии

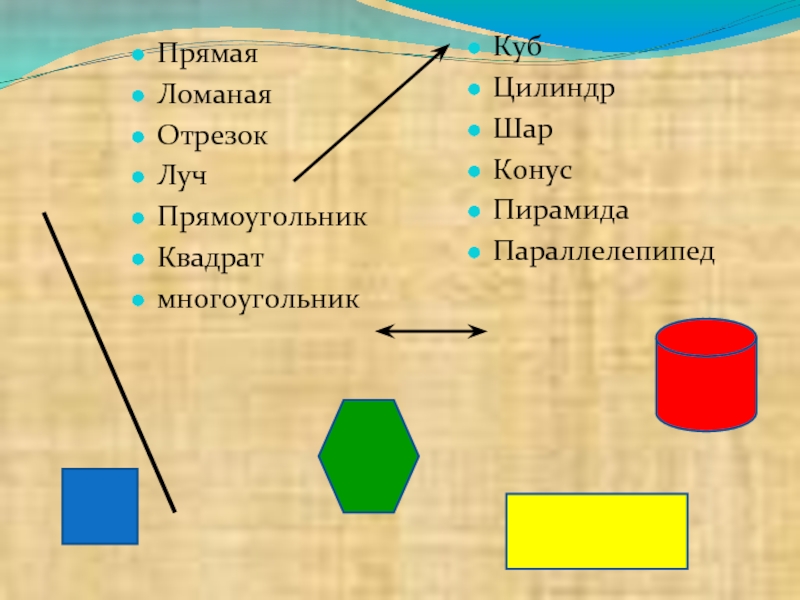
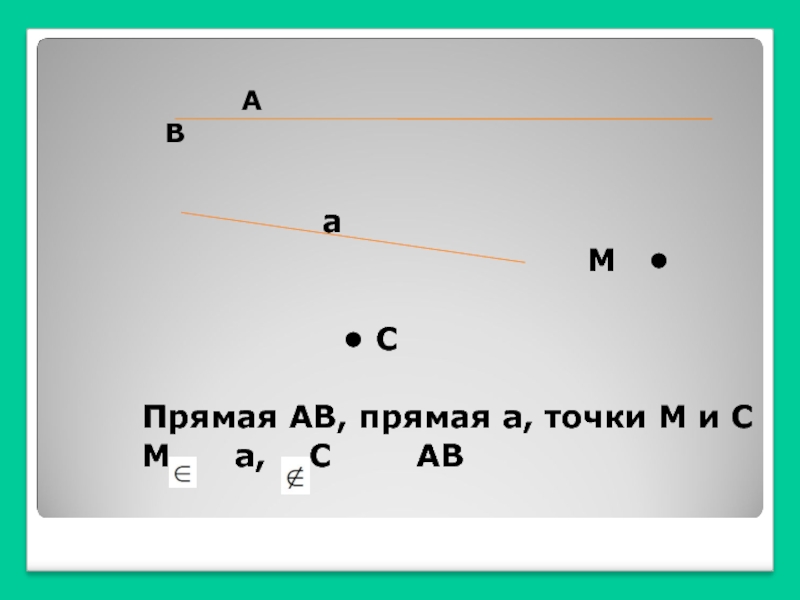
нужно было сооружать жилища, храмы, прокладывать дороги, оросительные каналы, устанавливать

границы земельных участков и определять их размеры. В переводе с греческого слово «геометрия» означает «землемерие» («гео» - по-гречески земля, а «метрео» - мерить). Такое название объясняется тем, что зарождение геометрии было связано с различными измерительными работами.
Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений.
За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания, которые добывались в основном опытным путем, но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построения прямых углов и т. д.

представляло собой научной теории.
Первым, кто начал получать геометрические факты при

помощи рассуждений (доказательств), был древнегреческий математик Фалес (VI в. до н. э.), который в своих исследованиях применял перегибание чертежа, поворот части фигуры и так далее, то есть то, что на современном геометрическом языке называется движением.
Постепенно геометрия становится наукой, в которой большинство фактов устанавливается путем выводов, рассуждений, доказательств.
Попытки греческих ученых привести геометрические факты в систему начинаются уже с V в. до н. э. Наибольшее влияние на всё последующее развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в III в. до н. э. Сочинение Евклида «Начала» почти 2000 лет служило основной книгой, по которой изучали геометрию. В «Началах» были систематизированы известные к тому времени геометрические сведения, и геометрия впервые предстала как математическая наука.

сама геометрия, изложенная в ней, стала называться евклидовой геометрией.
В геометрии

изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, цвета и т. д. Отвлекаясь от этих свойств и беря во внимание только форму и размеры предметов, мы приходим к понятию геометрической фигуры.
На уроках математики вы познакомились с некоторыми геометрическими фигурами и представляете себе, что такое точка, прямая, отрезок, луч, угол, как они могут быть расположены относительно друг друга. Вы знакомы с такими фигурами, как треугольник, прямоугольник, круг.
Геометрия не только дает представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, то есть логически мыслить.

как отрезок, луч, прямая, угол, окружность, круг, треугольник, прямоугольник, являются

плоскими, то есть целиком укладываются на плоскости.
Раздел геометрии, изучающий свойства фигур на плоскости, называется планиметрией (от латинского слова «планум» - плоскость и греческого «метрео» -измеряю).
В стереометрии изучаются свойства фигур в пространстве, таких как
параллелепипед,
шар,
цилиндр,
пирамида
Мы начнем изучение геометрии с планиметрии.

В


а
М •

• С

Прямая АВ, прямая а, точки М и С
М а, С АВ

через данную точку?
Сколько прямых можно провести через две данные

точки?


Выполните задания № 2, 3

О лежит на прямой АВ1?
Даны две прямые а и b,

пересекающиеся в точке С, и точка D, отличная от точки С и лежащая на прямой а. Может ли точка D лежать на прямой b?

лежащую на прямой p.
Отметьте точку D, не лежащую на прямой

p.
Используя символы е и е, запишите предложение: «Точка М лежит на прямой p, а точка D не лежит на ней».

2. Начертите прямые а й m, пересекающиеся в точке K. На прямой а отметьте точку С, отличную от точки К.
Являются ли прямые КС и а различными прямыми? Ответ обоснуйте.
Может ли прямая в проходить через точку С ? Ответ обоснуйте.

возможные случаи и сделайте соответствующие рисунки.
4*. На плоскости даны три

точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки.

общих точек могут иметь две прямые?
3. Какая фигура называется отрезком?
4.

Как обозначаются точки и прямые на рисунке?

25 учебника;
практические задания № 4, 6 и 7.