Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение комбинированных задач с помощью графов
Содержание
- 1. Решение комбинированных задач с помощью графов
- 2. Вопросы к уроку.Чем занимается комбинаторика?Что такое граф?Какие
- 3. 1.Чем занимается комбинаторика?Комбинаторика-раздел математики ,рассматривающий вопросы(задачи), связанные
- 4. 2.Что такое граф?Граф-геометрическая фигура,состоящая из точек(вершины графа) и линий,их соединяющих(рёбра графа).
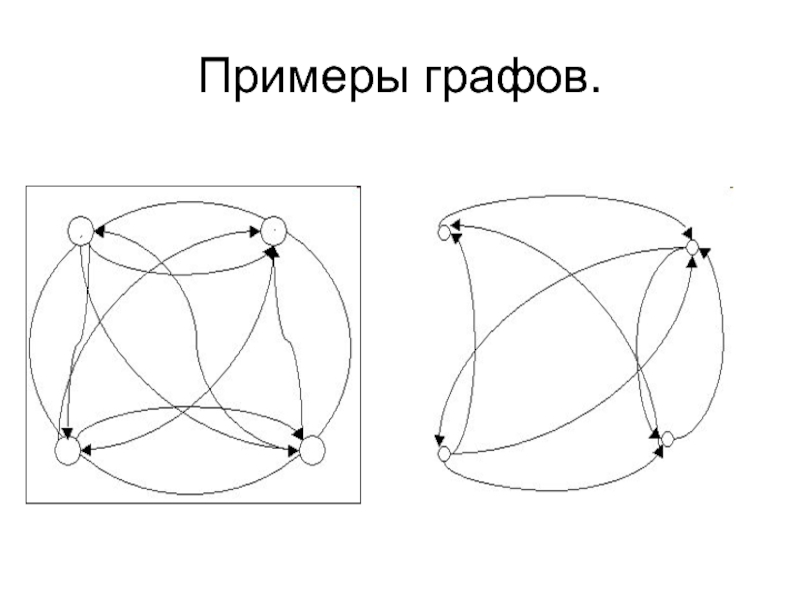
- 5. Примеры графов.
- 6. Примеры графов
- 7. Задача №1 Андрей, Борис, Виктор и
- 8. Задача №2
- 9. Задача №3 У Лёвы 2 конверта: обычный
- 10. Задача №4 Ужасные грабители Кнопка и
- 11. Задача №5 Сколько двузначных чисел можно составить
- 12. Задача № Сколько трёхзначных чисел можно составить
- 13. 1
- 14. Слайд 14
- 15. Задача № Сколько трёхзначных
- 16. Задача №(устно) Сколькими способами Петя и Вова
- 17. «Правило произведения».Если существует n вариантов выбора первого
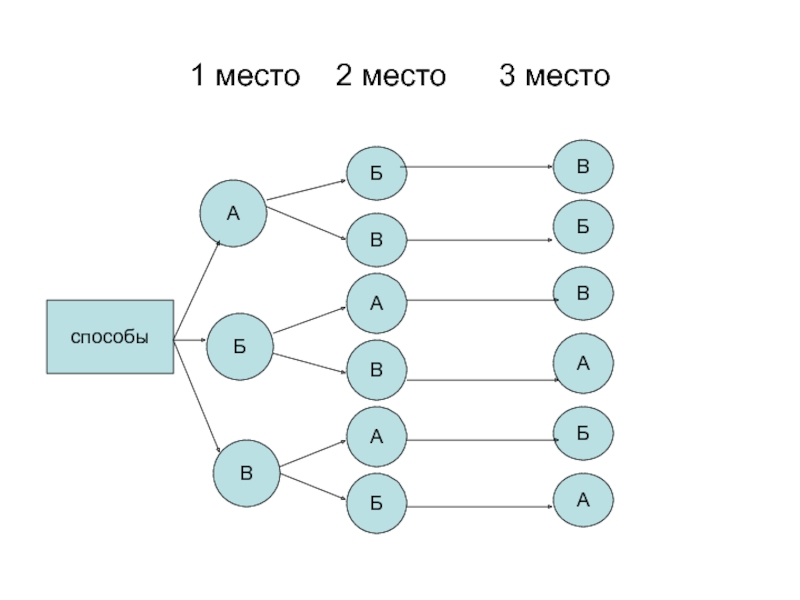
- 18. Задача № №.Антон, Борис и Василий купили
- 19. 1 место 2 место 3 место способыАБВБВАВАБВБВАБА
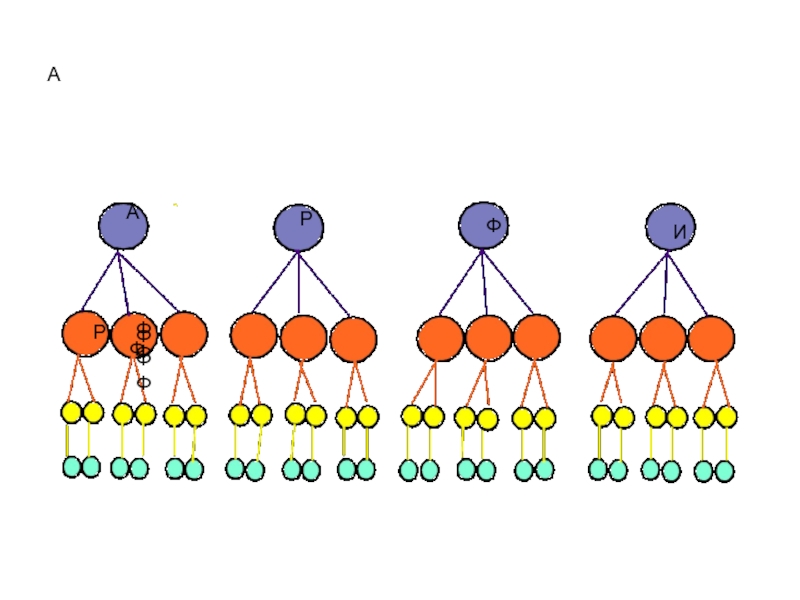
- 20. Задача №№.В пятницу у вас 4 уроков:
- 21. ААРФИРФФФФФФ
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Вопросы к уроку.
Чем занимается комбинаторика?
Что такое граф?
Какие задачи относятся к
комбинаторным?
Слайд 31.Чем занимается комбинаторика?
Комбинаторика-раздел математики ,рассматривающий вопросы(задачи), связанные с подсчётом числа
всевозможных комбинаций из элементов данного конечного множества при сделанных исходных
предположениях.Слайд 42.Что такое граф?
Граф-геометрическая фигура,состоящая из точек(вершины графа) и линий,их соединяющих(рёбра
графа).
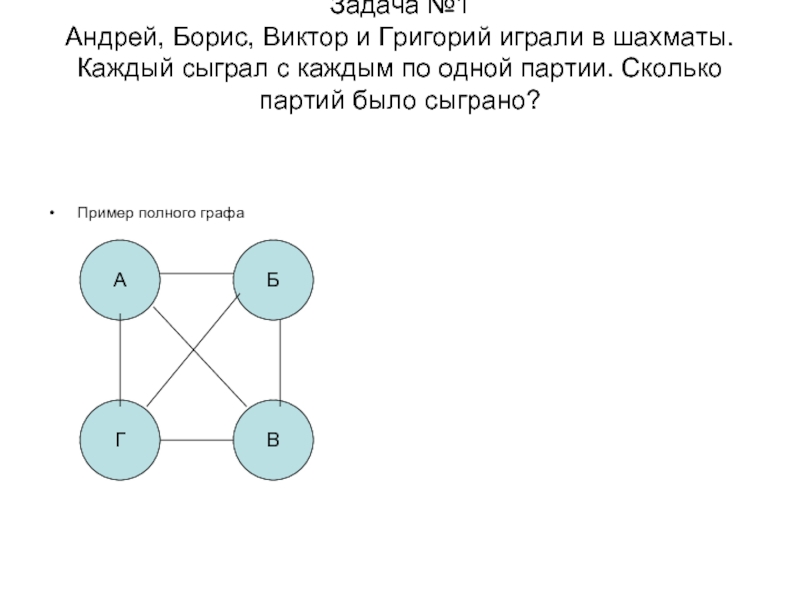
Слайд 7 Задача №1 Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый
сыграл с каждым по одной партии. Сколько партий было сыграно?
Пример
полного графаА
Б
Г
В
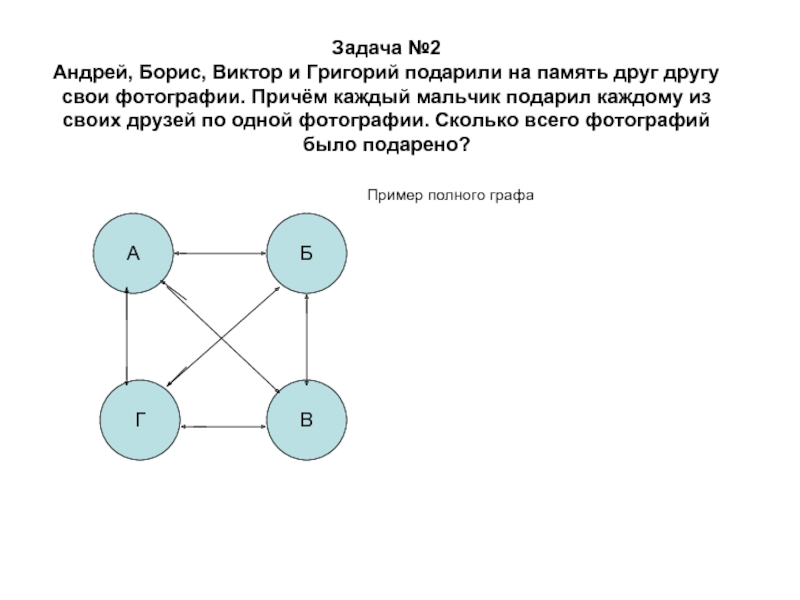
Слайд 8 Задача №2 Андрей, Борис, Виктор и Григорий подарили на память друг
другу свои фотографии. Причём каждый мальчик подарил каждому из своих
друзей по одной фотографии. Сколько всего фотографий было подарено? Пример полного графаА
Г
Б
В
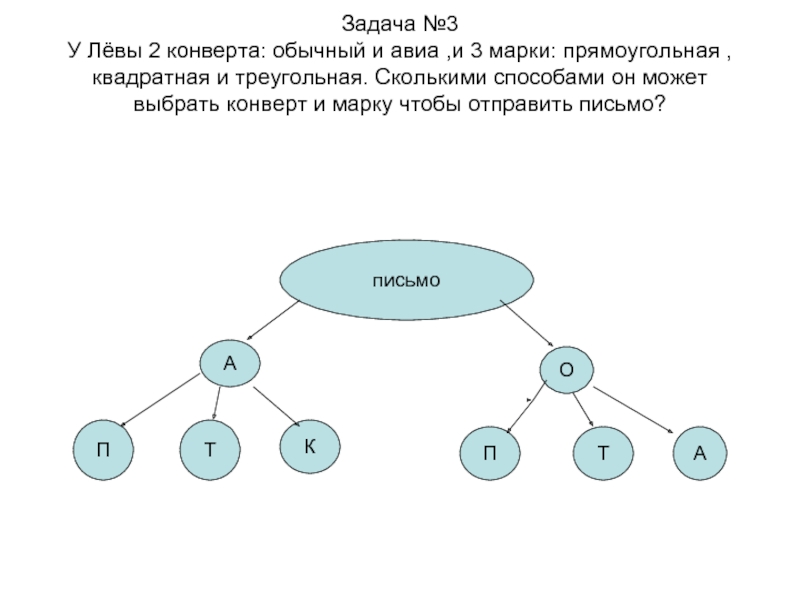
Слайд 9Задача №3 У Лёвы 2 конверта: обычный и авиа ,и 3
марки: прямоугольная , квадратная и треугольная. Сколькими способами он может
выбрать конверт и марку чтобы отправить письмо?письмо
А
О
П
Т
К
П
Т
А
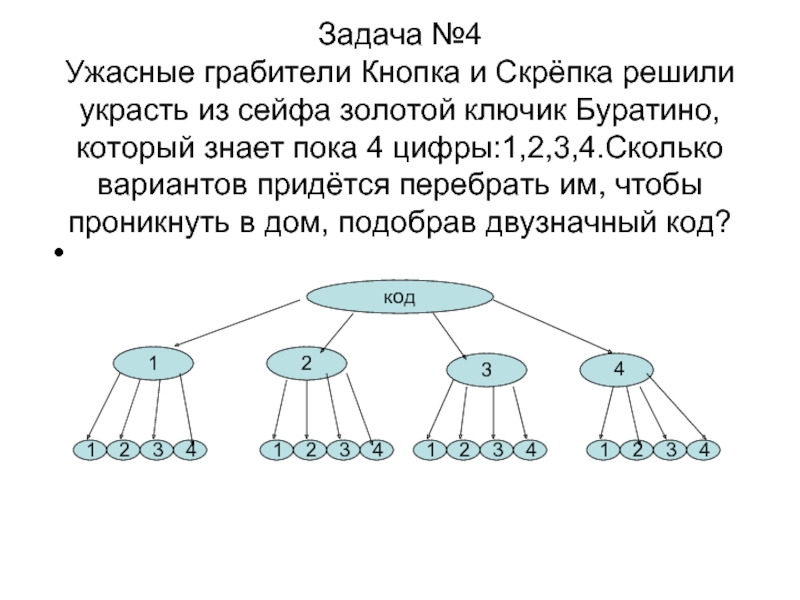
Слайд 10 Задача №4 Ужасные грабители Кнопка и Скрёпка решили украсть из сейфа
золотой ключик Буратино, который знает пока 4 цифры:1,2,3,4.Сколько вариантов придётся
перебрать им, чтобы проникнуть в дом, подобрав двузначный код?
код
1
2
3
1
2
4
3
1
2
3
4
1
2
3
4
1
2
3
4
4
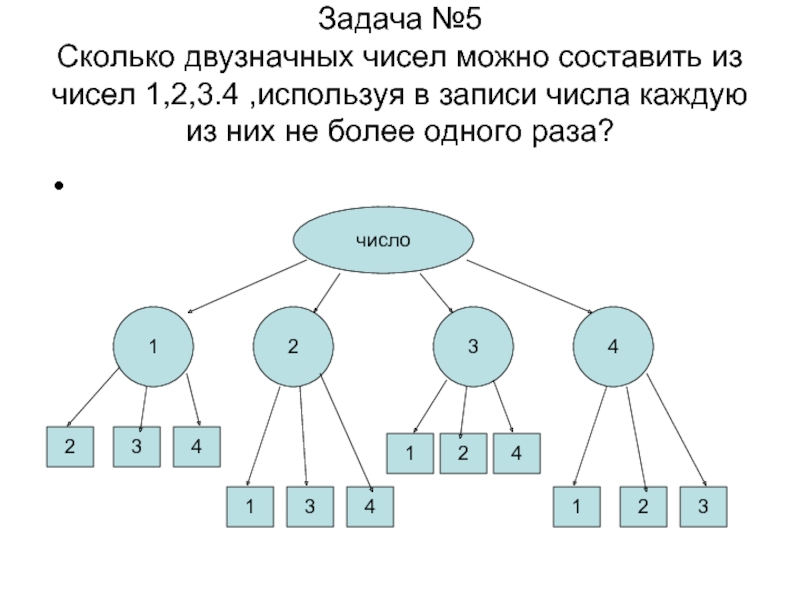
Слайд 11Задача №5 Сколько двузначных чисел можно составить из чисел 1,2,3.4 ,используя
в записи числа каждую из них не более одного раза?
число
1
2
3
4
2
3
4
1
3
4
1
2
4
1
2
3
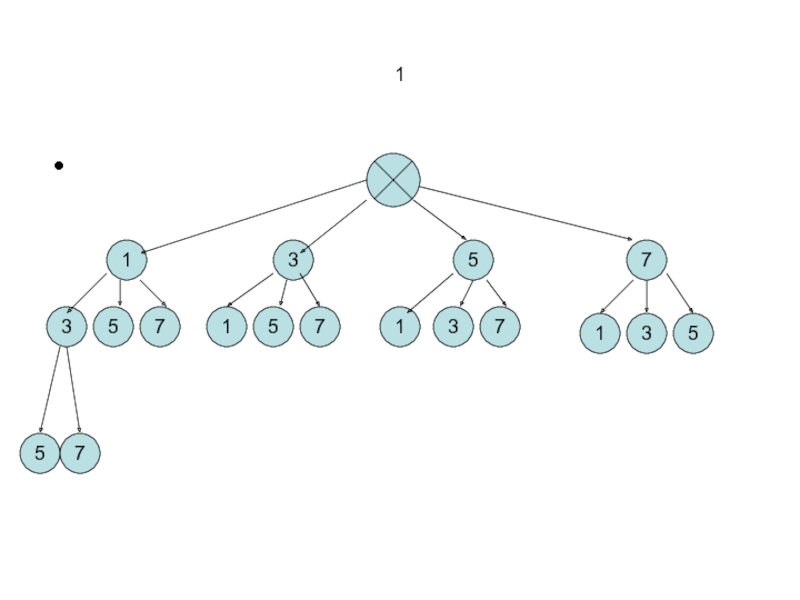
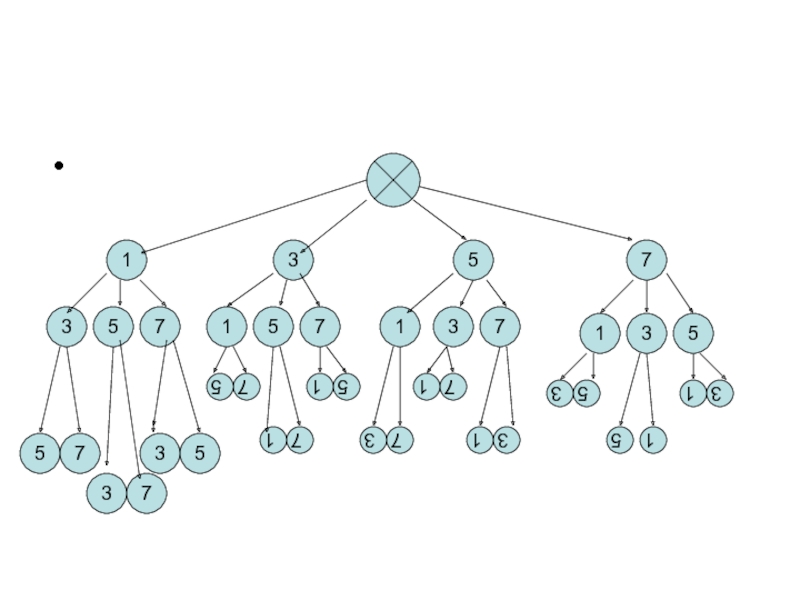
Слайд 12Задача № Сколько трёхзначных чисел можно составить из цифр 1,3,5,7, используя
в записи числа каждую из них не более одного раза?
Слайд 15 Задача № Сколько трёхзначных чисел можно записать из цифр 1,2,3 при
условии ,что 1)цифры в записи числа должны быть различны;2)цифры в
записи числа могут повторяться?
Слайд 16Задача №(устно) Сколькими способами Петя и Вова могут занять
места за двухместной партой?
Сколькими способами вы можете рассадить
3-х гостей на 3-х разноцветных табуретках.№. Сколькими способами вы можете рассадить 4-х гостей на 4-х разноцветных табуретках?
№.Сколькими способами вы можете рассадить 5-х гостей на 5-х разноцветных табуретках?