Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема о соотношениях между сторонами и углами треугольника
Содержание
- 1. Теорема о соотношениях между сторонами и углами треугольника
- 2. Геометрию интересуют соотношения между элементами треугольникаКакие виды
- 3. ТеоремаВ треугольнике:против большей стороны лежит больший угол;против
- 4. Поиск способа доказательстваАВС I. В математике часто,
- 5. Работа по учебнику с доказательствомИзучите доказательство, предложенное
- 6. Оформление доказательстваОформите доказательство теоремыСравните свое доказательство с предложенным и сделайте выводы
- 7. Итоги работыС какими фактами познакомились?В треугольнике:Против большей
- 8. Скачать презентанцию
Геометрию интересуют соотношения между элементами треугольникаКакие виды треугольников вы знаете?Какое соотношение, связанное с углами треугольника вам известно?Сумма углов треугольника равна 180°Выясним соотношения между сторонами и углами треугольника
Слайды и текст этой презентации
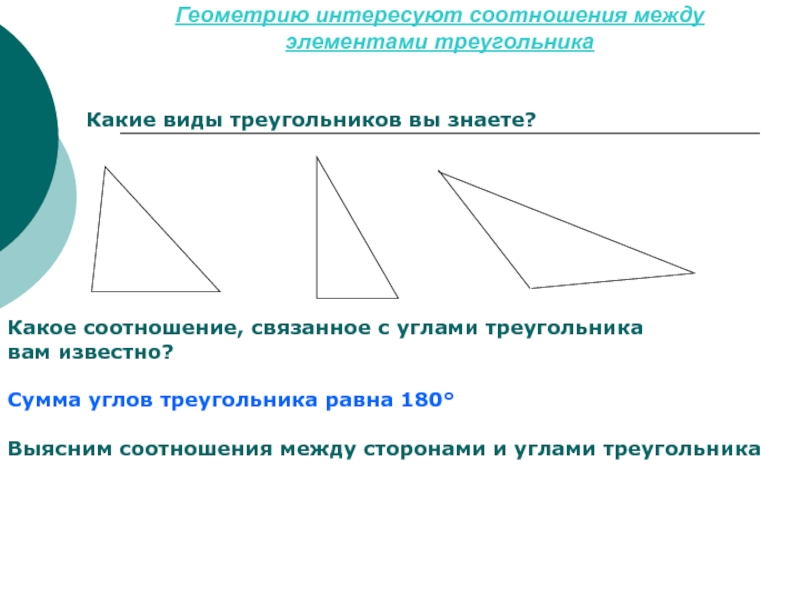
Слайд 2Геометрию интересуют соотношения между элементами треугольника
Какие виды треугольников вы знаете?
Какое
соотношение, связанное с углами треугольника
вам известно?
Сумма углов треугольника равна
180°Выясним соотношения между сторонами и углами треугольника
Слайд 3Теорема
В треугольнике:
против большей стороны лежит больший угол;
против большего угла лежит
большая сторона.
О какой фигуре идет речь в теореме?
Соотношения каких
элементоврассматриваются в первой части
теоремы?
Дано:
ΔАВС;
1) АВ – большая сторона.
Доказать, что ∠С - больший.
2) ∠С – наибольший.
Доказать, что АВ – большая сторона.
В
С
А
Что требуется доказать в первой части
теоремы?
рассматриваются во второй части
Что требуется доказать во второй части
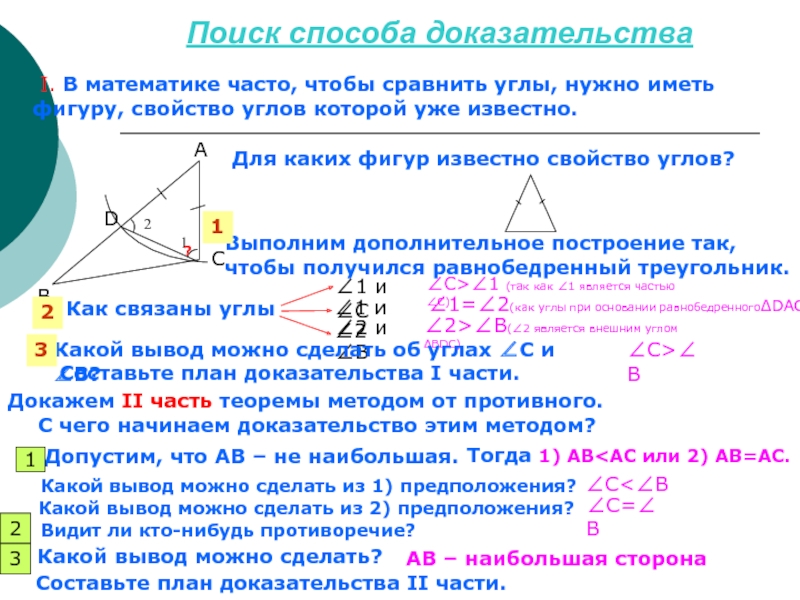
Слайд 4Поиск способа доказательства
А
В
С
I. В математике часто, чтобы сравнить углы,
нужно иметь
фигуру, свойство углов которой уже известно.
Для каких фигур
известно свойство углов?Выполним дополнительное построение так,
чтобы получился равнобедренный треугольник.
D
1
2
Как связаны углы
∠1 и ∠С
∠1 и ∠2
∠2 и ∠В
∠С>∠1 (так как ∠1 является частью ∠С)
∠1=∠2(как углы при основании равнобедренногоΔDАС)
∠2>∠В(∠2 является внешним углом ΔВDС)
Какой вывод можно сделать об углах ∠С и ∠В?
∠С>∠В
Докажем II часть теоремы методом от противного.
Составьте план доказательства I части.
1
2
3
С чего начинаем доказательство этим методом?
Тогда 1) АВ<АС или 2) АВ=АС.
Какой вывод можно сделать из 1) предположения?
∠С<∠В
∠С=∠В
Видит ли кто-нибудь противоречие?
Составьте план доказательства II части.
?
Допустим, что АВ – не наибольшая.
Какой вывод можно сделать из 2) предположения?
1
2
3
Какой вывод можно сделать?
АВ – наибольшая сторона
Слайд 5Работа по учебнику с доказательством
Изучите доказательство, предложенное в школьном учебнике
Назовите
основной прием, используемый при доказательстве первой части теоремы?
Выделите основные этапы
доказательства первой части теоремы? Метод от противного.
1
2
3
Выделите основные этапы доказательства второй части теоремы?
1
2
3
Назовите основные приемы, используемый при доказательстве теоремы?
Назовите основные прием, используемый при доказательстве второй части теоремы?
метод использования фигуры, свойство углов которой известно
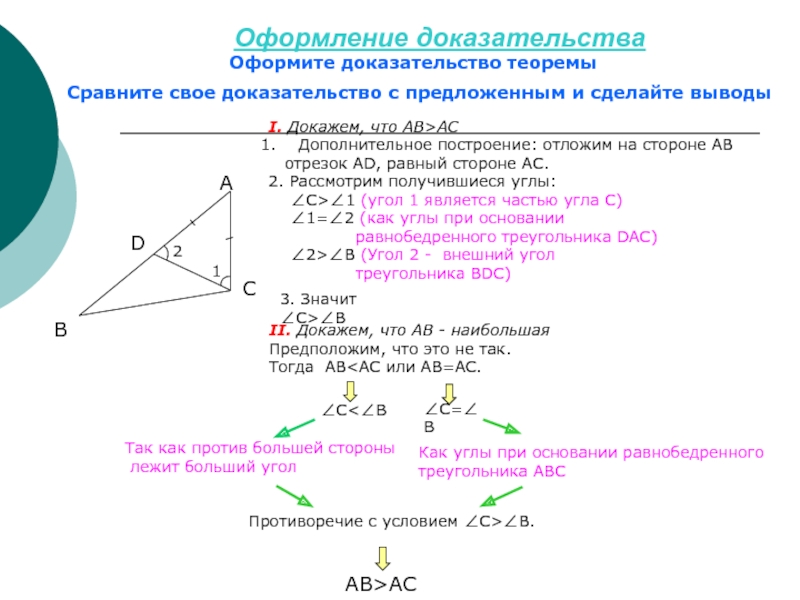
Слайд 6Оформление доказательства
Оформите доказательство теоремы
Сравните свое доказательство с предложенным и сделайте
выводы
Слайд 7Итоги работы
С какими фактами познакомились?
В треугольнике:
Против большей стороны лежит больший
угол;
Против большего угла лежит большая сторона.
Какую фигуру характеризует данные факты?
Треугольник.
Можно ли назвать данную теорему свойством треугольника?
Да, так как в условии теоремы сказано о треугольнике.
Что полезно запомнить из работы с теоремой?
При изучении доказательства, предложенного в учебнике,
полезно выделить этапы доказательства;
2. Геометрию интересуют соотношения между элементами
фигуры;
3. При доказательстве утверждений, связанных с
расположением углов в треугольнике используют метод
от противного;
4. В математике, чтобы сравнить углы, удобно иметь фигуру,
свойства углов которой уже известно.
