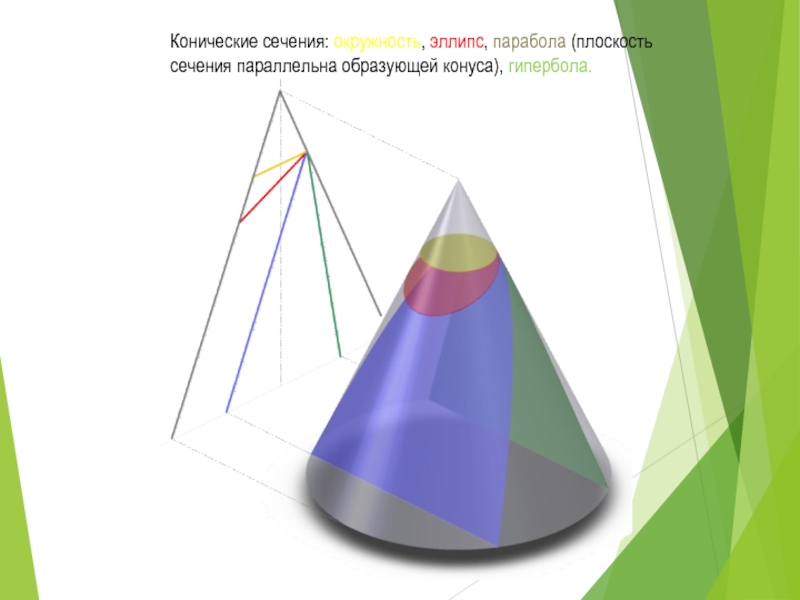
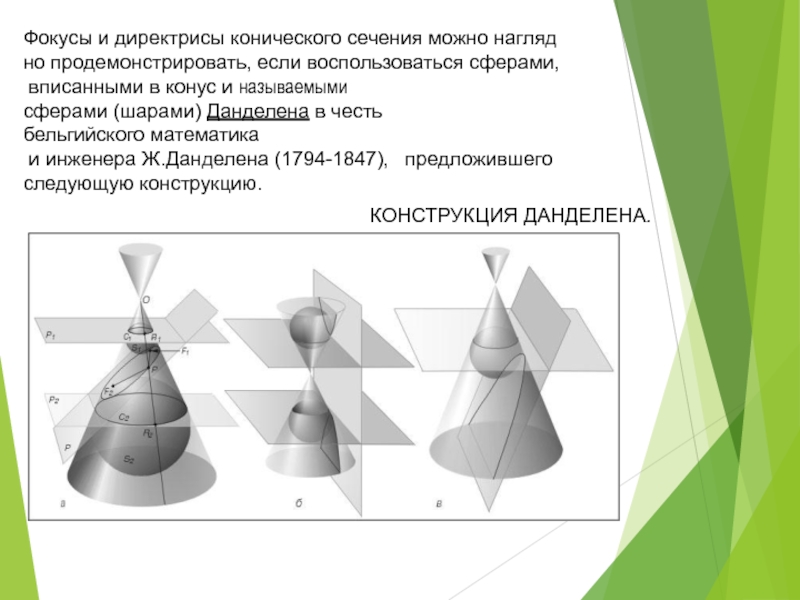
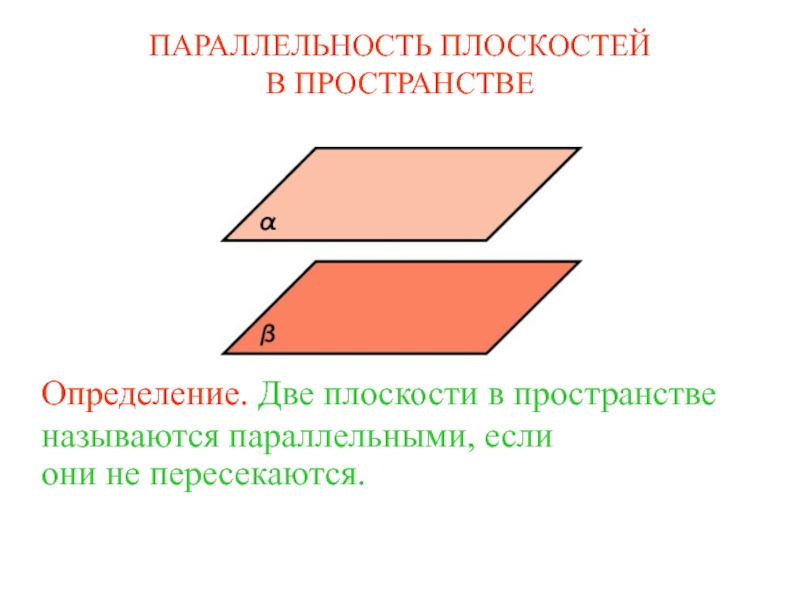
Конические сечения 11 класс

конических сечений: эллипс, парабола и гипербола, кроме того существуют вырожденные сечения: точка, прямая и пара прямых.

Открывателем конических сечений предположительно считается Менехм,ученик Платона и учитель Александра Македонского.

Аполлоний Пергский – ученый , который изучал конические сечения.

проблемой легко понять: для удвоения куба требуется извлечение кубического корня, а

оно недостижимо с помощью циркуля и линейки; однако если в класс допустимых кривых (прямые и окружности) добавить конические сечения, то построение кубических корней выполнить несложно. Алгебраически это означает, например, что для решения уравнения 
x3 =a мы находим точку пересечения кривых  y=x2  (парабола)  и y= a/x (гипербола).

через вершину конуса и точки окружности основания конуса.
Сечения конической

поверхности плоскостью можно рассматривать как центральную проекцию окружности основания конуса на эту плоскость. Поэтому, если плоскость параллельна плоскости основания и не проходит через вершину конуса, то в сечении конической поверхности получается окружность.

между образующей и этой осью, то в сечении конической поверхности

получается эллипс.