Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрия.Введение. Аксиоматика.
Содержание
- 1. Геометрия.Введение. Аксиоматика.
- 2. Слайд 2
- 3. IV – V вв. до н.э. – ПИФАГОРЕЙСКАЯ ШКОЛАПЕНТОГРАММА
- 4. М е ф и с т о
- 5. Египетский
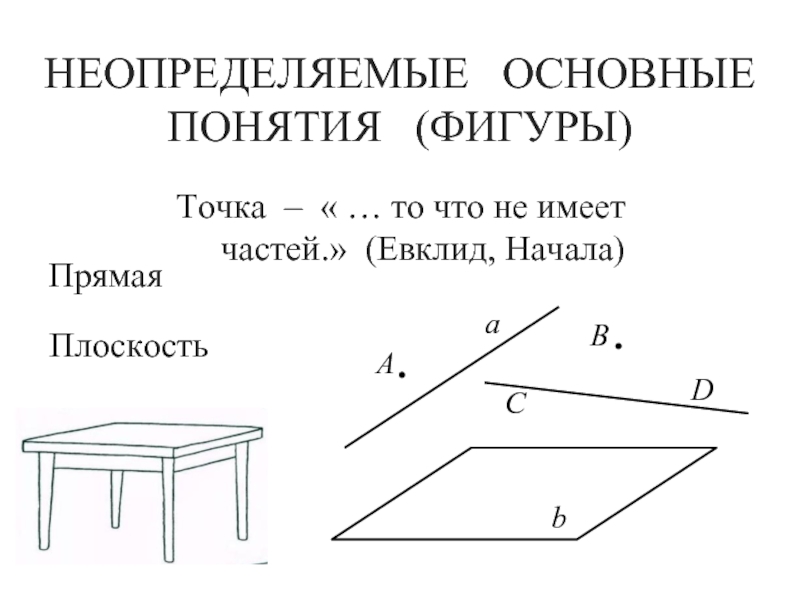
- 6. НЕОПРЕДЕЛЯЕМЫЕ ОСНОВНЫЕ ПОНЯТИЯ (ФИГУРЫ)Точка –
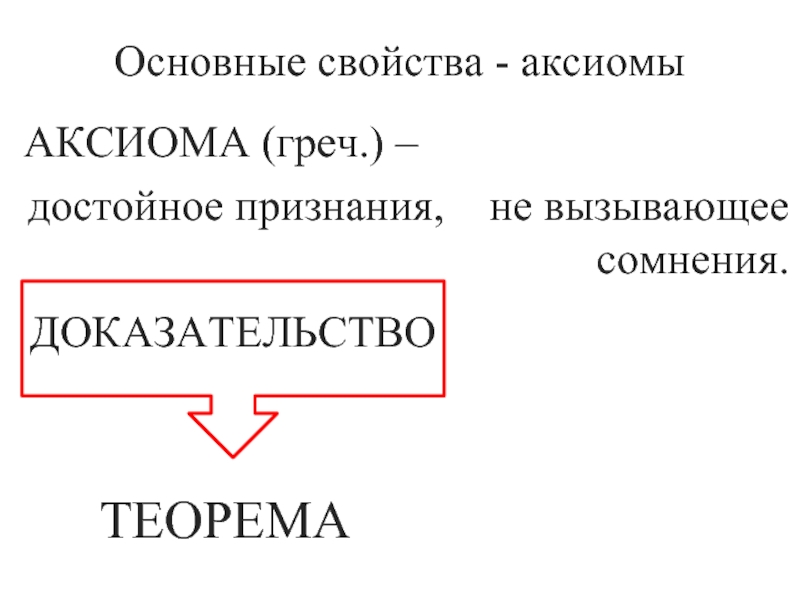
- 7. АКСИОМА (греч.) – достойное признания, не вызывающее сомнения. Основные свойства - аксиомыДОКАЗАТЕЛЬСТВОТЕОРЕМА
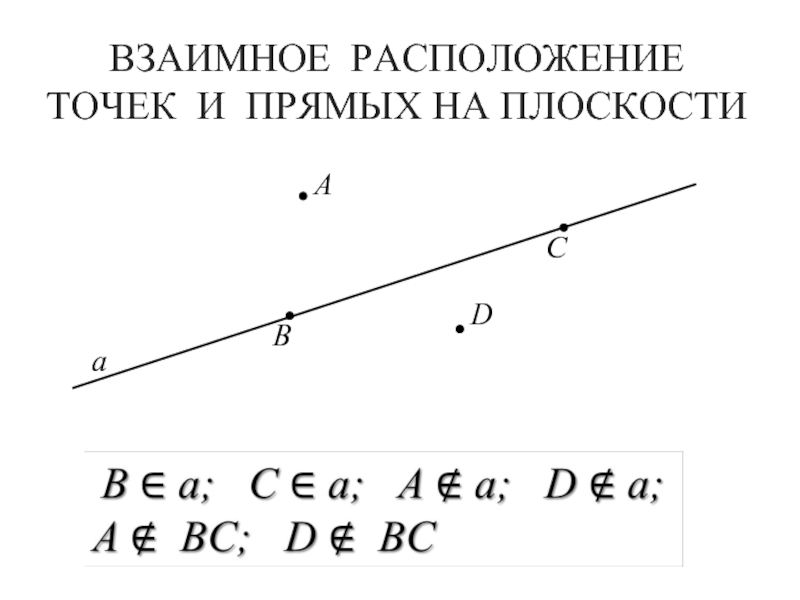
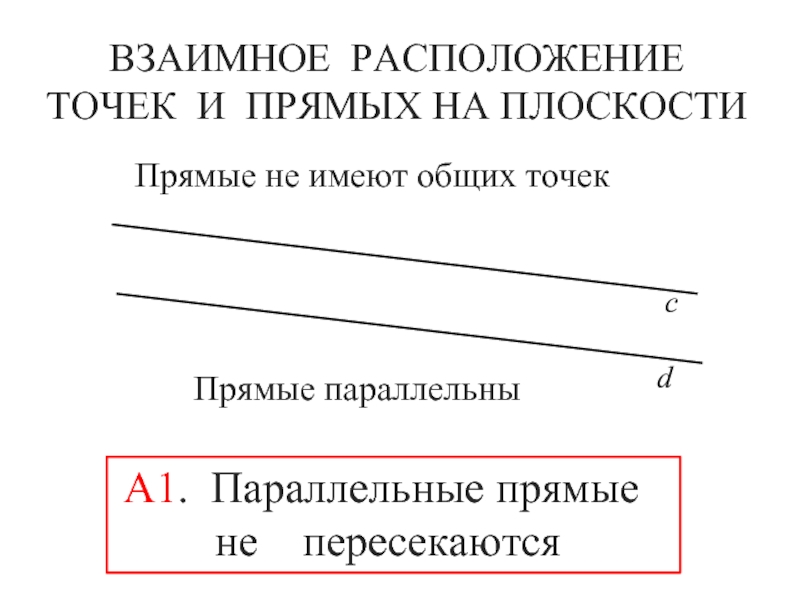
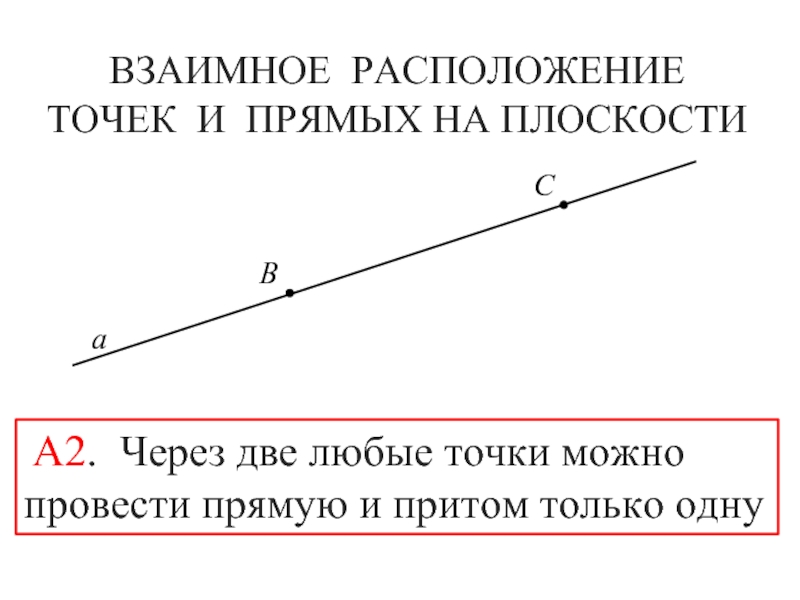
- 8. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИАBCDа
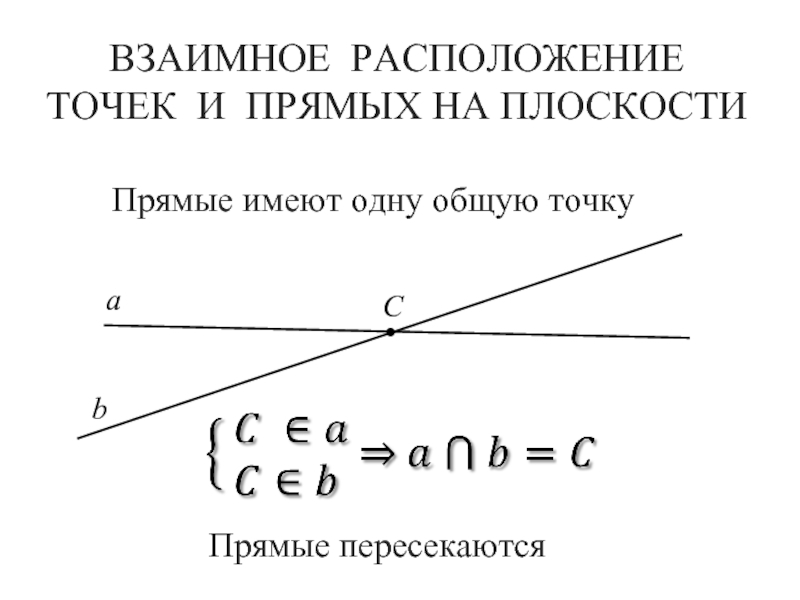
- 9. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИаbCПрямые пересекаютсяПрямые имеют одну общую точку
- 10. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИсdПрямые
- 11. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИBCа
- 12. Провести четыре прямые так чтобы каждые две
- 13. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИСколько
- 14. Сколько прямых можно провести череза) три точкиб)
- 15. Домашнее задание СПАСИБО ЗА РАБОТУ !
- 16. Скачать презентанцию
IV – V вв. до н.э. – ПИФАГОРЕЙСКАЯ ШКОЛАПЕНТОГРАММА
Слайды и текст этой презентации
Слайд 1ГЕОМЕТРИЯ
Гео – земля
Метрео – измеряю
(греч.)
Волконская Н.Н . ГБОУ
школа № 644 Санкт-Петербург
Слайд 4М е ф и с т о ф е л
ь:
Нет, трудновато выйти мне теперь
Тут кое-что
мешает мне немного:Волшебный знак у вашего порога.
Ф а у с т:
Не пентаграмма ль этому виной?
Но как же, бес, пробрался ты за мной?
Каким путем впросак попался?
М е ф и с т о ф е л ь:
Изволили ее вы плохо начертить,
И промежуток в уголку остался,
Там, у дверей, –
и я свободно мог вскочить.
Ф а у с т. Г е т е.