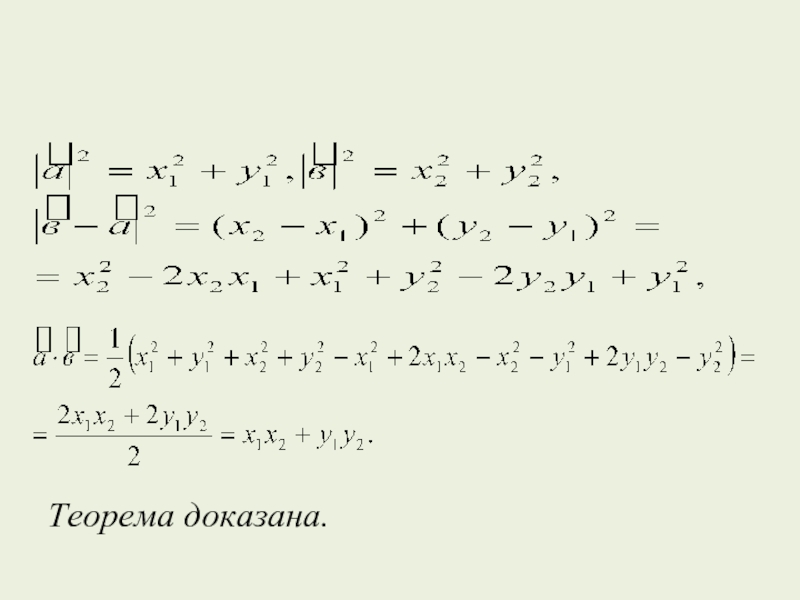Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Скалярное произведение в координатах
Содержание
- 1. Скалярное произведение в координатах
- 2. Теорема В прямоугольной системе координат скалярное произведение векторов выражается формулой
- 3. Слайд 3
- 4. Теорема доказана.
- 5. №1044(а)Дано:Найти:Решение.Ответ: -2,5.
- 6. Следствие 1. Ненулевые векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.№1047(а)Решение.
- 7. Следствие 2. Косинус угла между векторами выражается формулой Решение.
- 8. Свойства скалярного произведения векторов
- 9. Скачать презентанцию
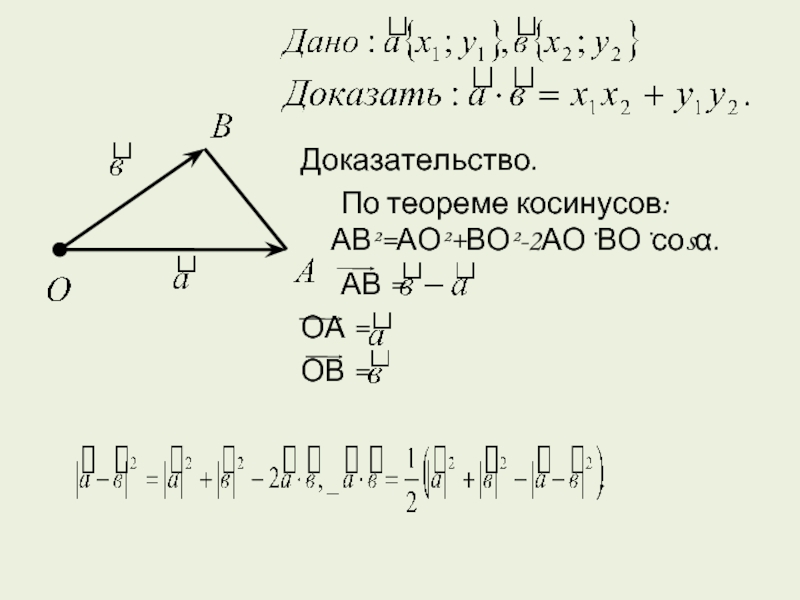
Теорема В прямоугольной системе координат скалярное произведение векторов выражается формулой
Слайды и текст этой презентации
Слайд 1Скалярное произведение
в координатах
Подготовила:
учитель математики
МОУ сош №30 имени А.И.Колдунова
Кутоманова Е.М.
2010-2011
учебный год
Слайд 2Теорема
В прямоугольной системе координат скалярное произведение векторов
выражается формулой
Слайд 6Следствие 1. Ненулевые векторы перпендикулярны тогда и только тогда, когда их
скалярное произведение равно нулю.
№1047(а)
Решение.
Теги