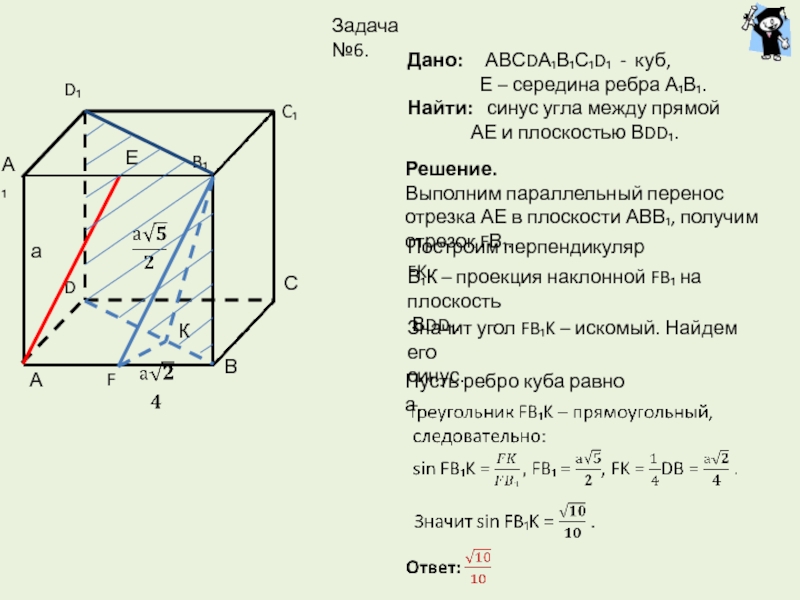
Е – середина ребра А₁В₁,
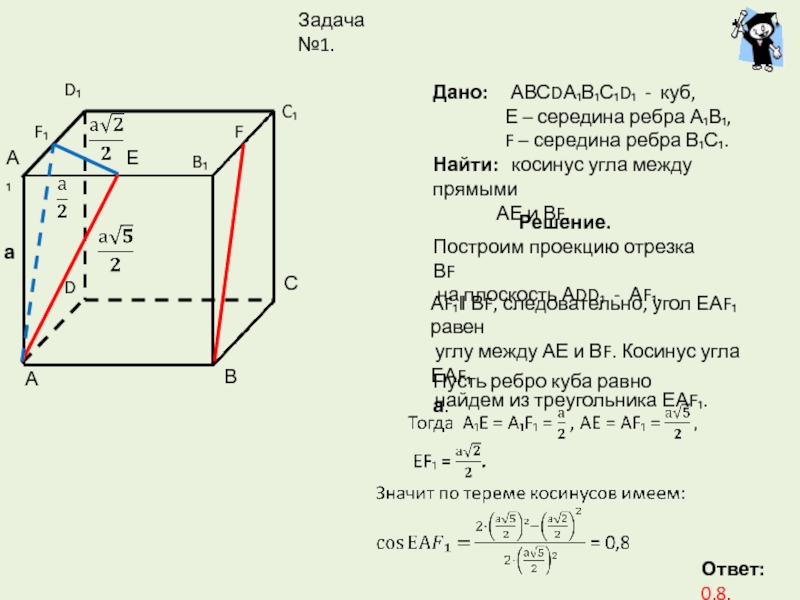
F – середина ребра В₁С₁.Найти: косинус угла между прямыми
АЕ и ВF.
Решение.
Построим проекцию отрезка ВF
на плоскость АDD₁ - АF₁.
F₁
АF₁ǁ ВF, следовательно, угол ЕАF₁ равен
углу между АЕ и ВF. Косинус угла ЕАF₁
найдем из треугольника ЕАF₁.
Пусть ребро куба равно а.
а
Ответ: 0,8.