Разделы презентаций

Построение сечений в многогранниках 10 класс

Содержание

Геометрические понятияПлоскость – граньПрямая – реброТочка – вершинаграньребровершина

Слайды и текст этой презентации

Слайд 1Многогранники
Тетраэдр
Параллелепипед

МногогранникиТетраэдрПараллелепипед

Слайд 2Геометрические понятия
Плоскость – грань
Прямая – ребро
Точка – вершина
грань
ребро
вершина

Геометрические понятияПлоскость – граньПрямая – реброТочка – вершинаграньребровершина

Слайд 3Кроссворд
Бесконечная ровная поверхность
Сторона грани многогранника.
Основное понятие геометрии – место пересечения

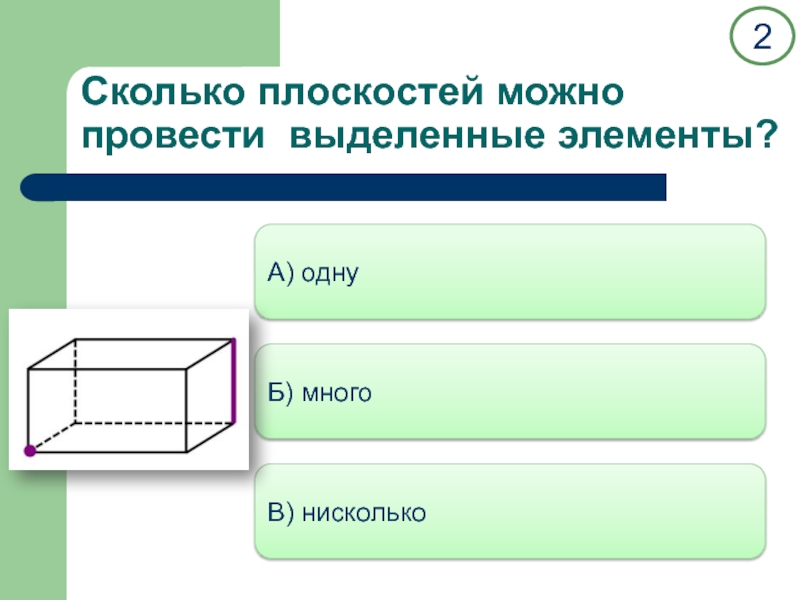
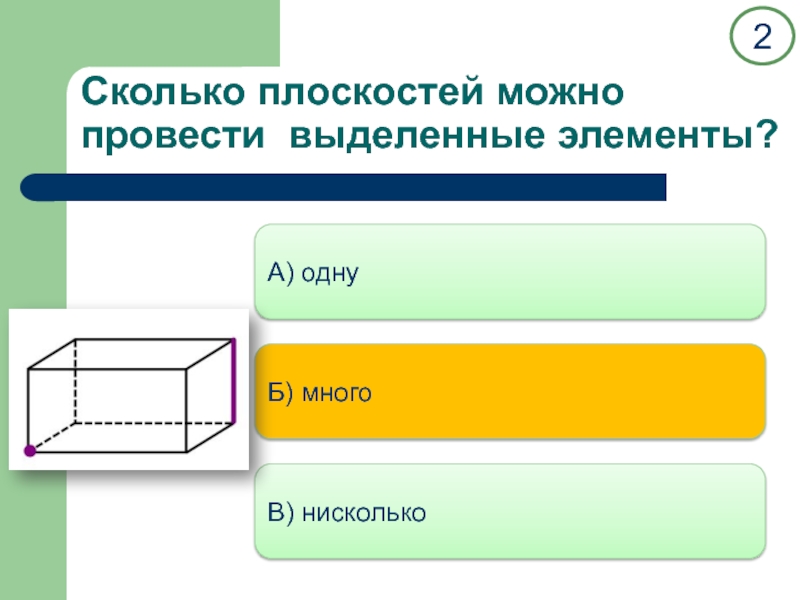
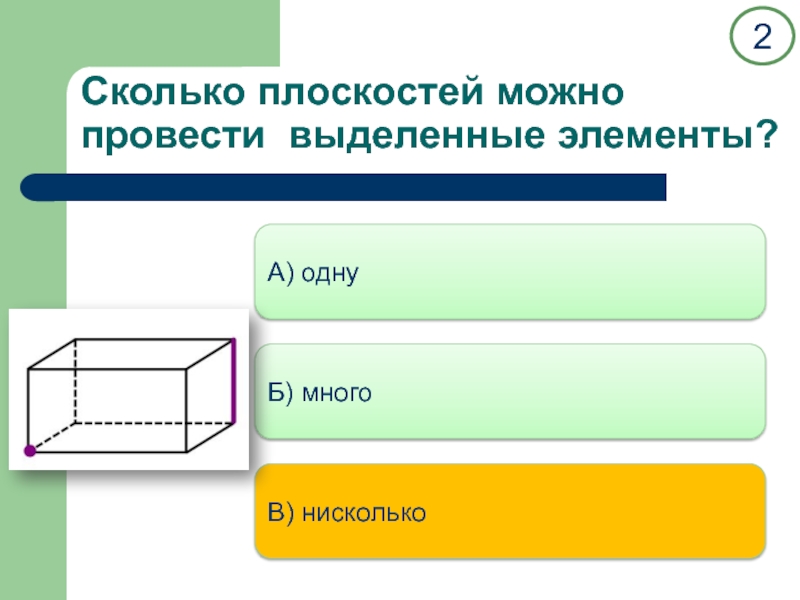
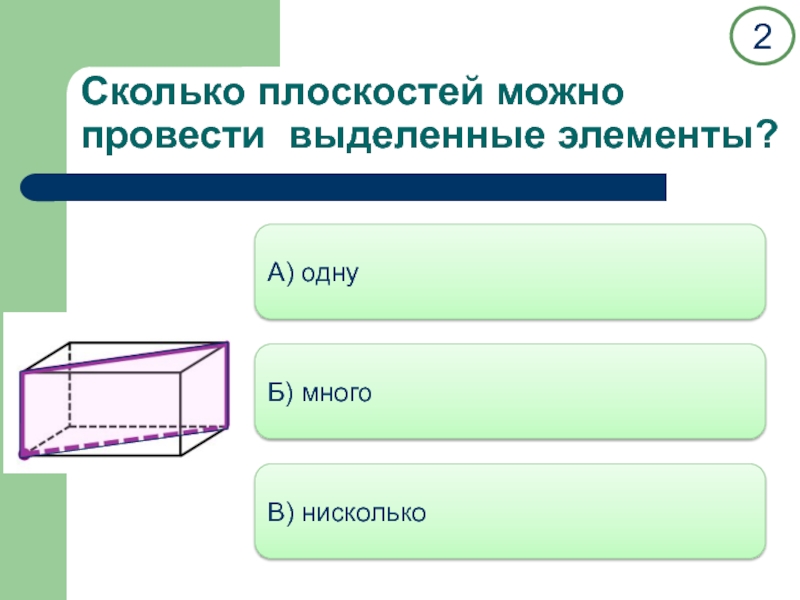
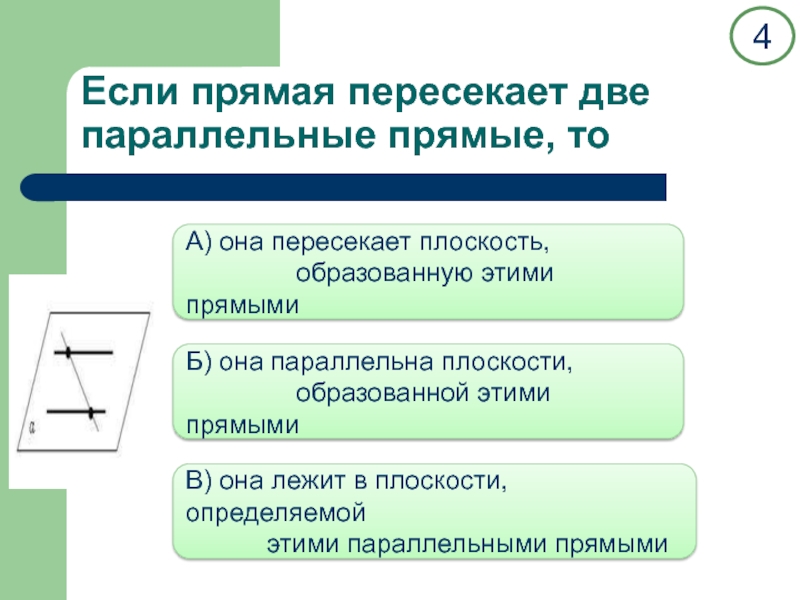
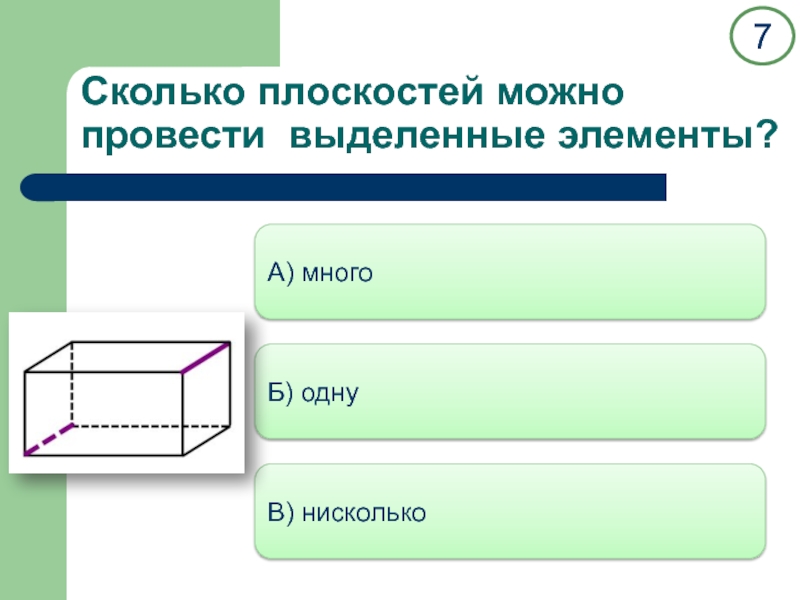
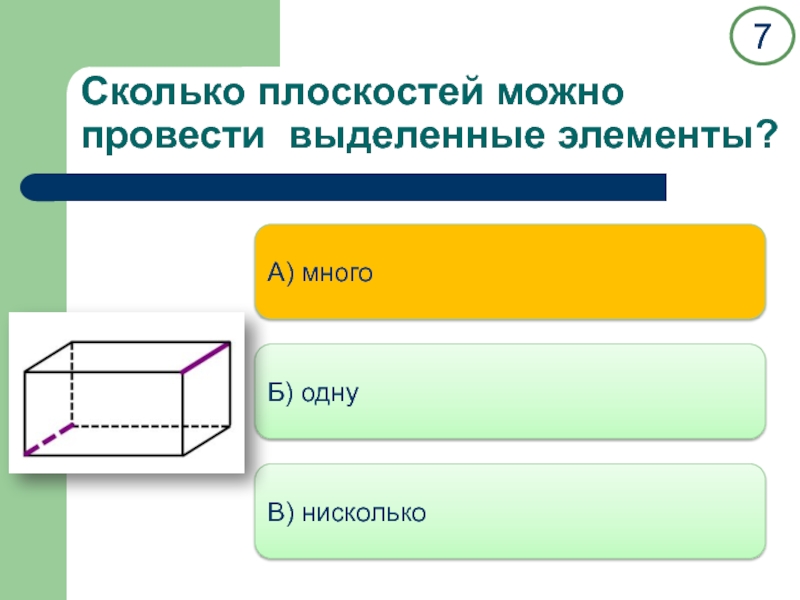
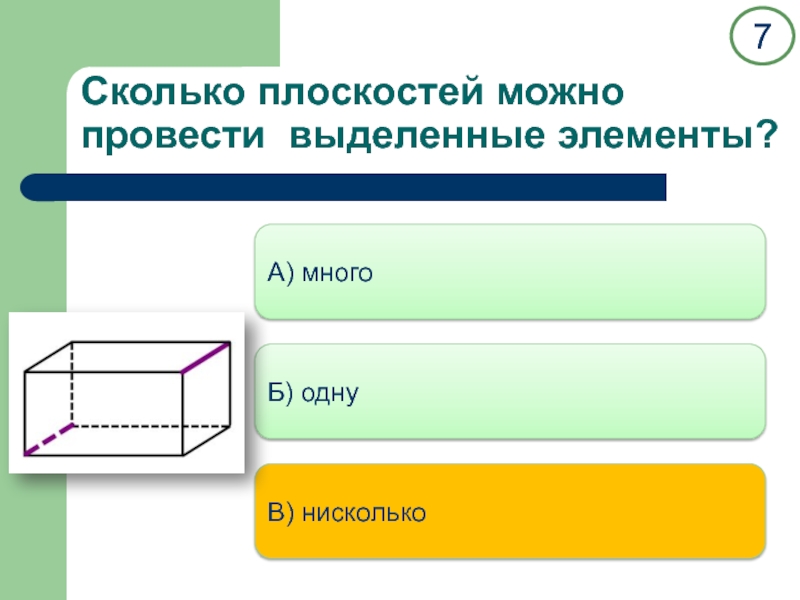
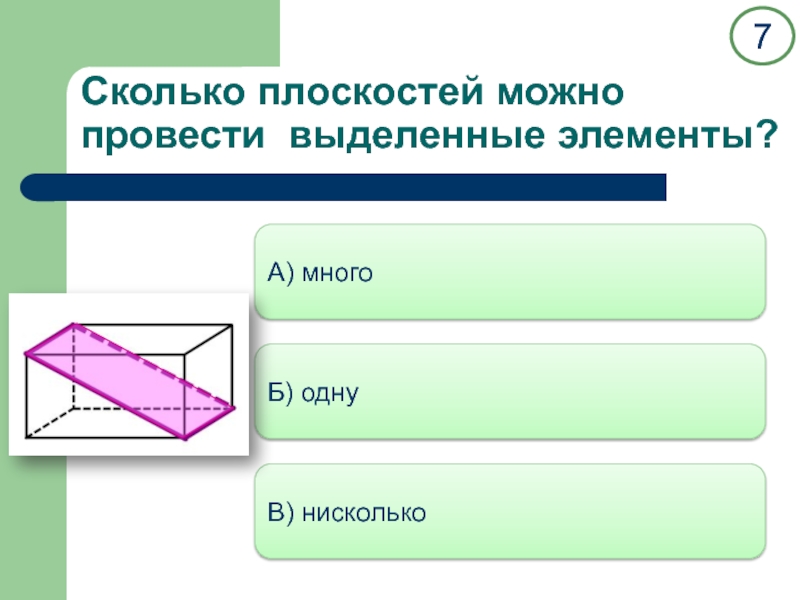
двух прямых.
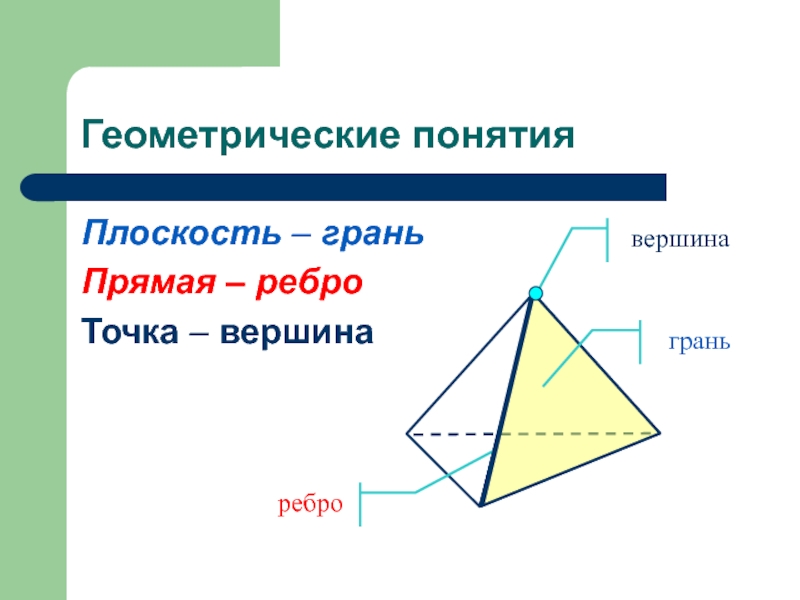
Точка пересечения ребер многогранника.
Сторона многогранника.
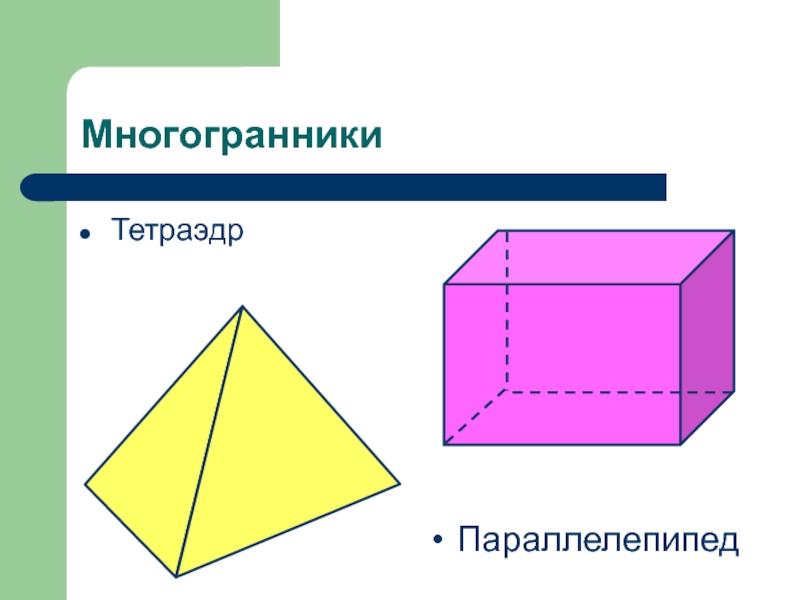
Поверхность, составленная из многоугольников.
Раздел

геометрии, изучающий фигуры в пространстве.

П

Л

О

С

К

О

Т

Ь

С

Р

Е

Б

Р

О

Т

Ч

К

О

А

Р

Ш

И

Н

А

В

Е

Г

Р

А

Н

Ь

О

Г

О

Г

Р

М

Н

Н

И

К

С

Т

А

Н

Е

О

М

Е

Т

Е

Р

Я

Р

И

КроссвордБесконечная ровная поверхностьСторона грани многогранника.Основное понятие геометрии – место пересечения двух прямых. Точка пересечения ребер многогранника.Сторона многогранника.Поверхность,

Слайд 4Построение сечений в многогранниках

Построение сечений в многогранниках

Слайд 5Сегодня на уроке:
Повторим геометрические понятия и утверждения.
Сформулируем правила для построения

сечения.
Отработаем умения построения сечений.

Сегодня на уроке:Повторим геометрические понятия и утверждения.Сформулируем правила для построения сечения. Отработаем умения построения сечений.

Слайд 6Если 2 плоскости имеют общую точку, то
А) они называются пересекающимися
Б)

они пересекаются по прямой,

проходящей через эту точку

В) они параллельны

1

Если 2 плоскости имеют общую точку, тоА) они называются пересекающимисяБ) они пересекаются по прямой,

Слайд 7Если 2 плоскости имеют общую точку, то
А) они называются пересекающимися
Б)

они пересекаются по прямой,

проходящей через эту точку

В) они параллельны

1

Если 2 плоскости имеют общую точку, тоА) они называются пересекающимисяБ) они пересекаются по прямой,

Слайд 8Если 2 плоскости имеют общую точку, то
А) они называются пересекающимися
Б)

они пересекаются по прямой,

проходящей через эту точку

В) они параллельны

1

Если 2 плоскости имеют общую точку, тоА) они называются пересекающимисяБ) они пересекаются по прямой,

Слайд 9Если 2 плоскости имеют общую точку, то
А) они называются пересекающимися
Б)

они пересекаются по прямой,

проходящей через эту точку

В) они параллельны

1

Если 2 плоскости имеют общую точку, тоА) они называются пересекающимисяБ) они пересекаются по прямой,

Слайд 10Сколько плоскостей можно провести выделенные элементы?
А) одну
Б) много
В) нисколько
2

Сколько плоскостей можно провести выделенные элементы?А) однуБ) многоВ) нисколько2

Слайд 11Сколько плоскостей можно провести выделенные элементы?
А) одну
Б) много
В) нисколько
2

Сколько плоскостей можно провести выделенные элементы?А) однуБ) многоВ) нисколько2

Слайд 12Сколько плоскостей можно провести выделенные элементы?
А) одну
Б) много
В) нисколько
2

Сколько плоскостей можно провести выделенные элементы?А) однуБ) многоВ) нисколько2

Слайд 13Сколько плоскостей можно провести выделенные элементы?
А) одну
Б) много
В) нисколько
2

Сколько плоскостей можно провести выделенные элементы?А) однуБ) многоВ) нисколько2

Слайд 14Через прямую и не лежащую на ней точку
А) проходит

плоскость и притом

только одна.

Б) проходит бесконечное количество
плоскостей

В) нельзя провести плоскость

3

Через прямую и не лежащую на ней точку А) проходит плоскость и притом

Слайд 15Через прямую и не лежащую на ней точку
А) проходит

плоскость и притом

только одна.

Б) проходит бесконечное количество
плоскостей

В) нельзя провести плоскость

3

Через прямую и не лежащую на ней точку А) проходит плоскость и притом

Слайд 16Через прямую и не лежащую на ней точку
А) проходит

плоскость и притом

только одна.

Б) проходит бесконечное количество
плоскостей

В) нельзя провести плоскость

3

Через прямую и не лежащую на ней точку А) проходит плоскость и притом

Слайд 17Через прямую и не лежащую на ней точку
А) проходит

плоскость и притом

только одна.

Б) проходит бесконечное количество
плоскостей

В) нельзя провести плоскость

3

Через прямую и не лежащую на ней точку А) проходит плоскость и притом

Слайд 18Если прямая пересекает две параллельные прямые, то
А) она пересекает плоскость,


образованную этими

прямыми

Б) она параллельна плоскости,
образованной этими прямыми

В) она лежит в плоскости, определяемой
этими параллельными прямыми

4

Если прямая пересекает две параллельные прямые, тоА) она пересекает плоскость,

Слайд 19Если прямая пересекает две параллельные прямые, то
А) она пересекает плоскость,


образованную этими

прямыми

Б) она параллельна плоскости,
образованной этими прямыми

В) она лежит в плоскости, определяемой
этими параллельными прямыми

2

4

Если прямая пересекает две параллельные прямые, тоА) она пересекает плоскость,

Слайд 20Если прямая пересекает две параллельные прямые, то
А) она пересекает плоскость,


образованную этими

прямыми

Б) она параллельна плоскости,
образованной этими прямыми

В) она лежит в плоскости, определяемой
этими параллельными прямыми

4

Если прямая пересекает две параллельные прямые, тоА) она пересекает плоскость,

Слайд 21Если прямая пересекает две параллельные прямые, то
А) она пересекает плоскость,


образованную этими

прямыми

Б) она параллельна плоскости,
образованной этими прямыми

В) она лежит в плоскости, определяемой
этими параллельными прямыми

4

Если прямая пересекает две параллельные прямые, тоА) она пересекает плоскость,

Слайд 22Две прямые называются скрещивающимися, если
А) они лежат в одной плоскости
Б)

они не пересекаются
В) они не пересекаются

и не параллельны

5

Две прямые называются скрещивающимися, еслиА) они лежат в одной плоскостиБ) они не пересекаютсяВ) они не пересекаются

Слайд 23Две прямые называются скрещивающимися, если
А) они лежат в одной плоскости
Б)

они не пересекаются
В) они не пересекаются

и не параллельны

5

Две прямые называются скрещивающимися, еслиА) они лежат в одной плоскостиБ) они не пересекаютсяВ) они не пересекаются

Слайд 24Две прямые называются скрещивающимися, если
А) они лежат в одной плоскости
Б)

они не пересекаются
В) они не пересекаются

и не параллельны

5

Две прямые называются скрещивающимися, еслиА) они лежат в одной плоскостиБ) они не пересекаютсяВ) они не пересекаются

Слайд 25Две прямые называются скрещивающимися, если
А) они лежат в одной плоскости
Б)

они не пересекаются
В) они не пересекаются

и не параллельны

5

Две прямые называются скрещивающимися, еслиА) они лежат в одной плоскостиБ) они не пересекаютсяВ) они не пересекаются

Слайд 26Если две прямые параллельны третей прямой, то
А) они параллельны
Б) они

лежат в одной плоскости
В) они скрещиваются
6

Если две прямые параллельны третей прямой, тоА) они параллельныБ) они лежат в одной плоскостиВ) они скрещиваются6

Слайд 27Если две прямые параллельны третей прямой, то
А) они параллельны
Б) они

лежат в одной плоскости
В) они скрещиваются
6

Если две прямые параллельны третей прямой, тоА) они параллельныБ) они лежат в одной плоскостиВ) они скрещиваются6

Слайд 28Если две прямые параллельны третей прямой, то
А) они параллельны
Б) они

лежат в одной плоскости
В) они скрещиваются
6

Если две прямые параллельны третей прямой, тоА) они параллельныБ) они лежат в одной плоскостиВ) они скрещиваются6

Слайд 29Если две прямые параллельны третей прямой, то
А) они параллельны
Б) они

лежат в одной плоскости
В) они скрещиваются
6

Если две прямые параллельны третей прямой, тоА) они параллельныБ) они лежат в одной плоскостиВ) они скрещиваются6

Слайд 30Сколько плоскостей можно провести выделенные элементы?
А) много
Б) одну
В) нисколько
7

Сколько плоскостей можно провести выделенные элементы?А) многоБ) однуВ) нисколько7

Слайд 31Сколько плоскостей можно провести выделенные элементы?
А) много
Б) одну
В) нисколько
7

Сколько плоскостей можно провести выделенные элементы?А) многоБ) однуВ) нисколько7

Слайд 32Сколько плоскостей можно провести выделенные элементы?
А) много
Б) одну
В) нисколько
7

Сколько плоскостей можно провести выделенные элементы?А) многоБ) однуВ) нисколько7

Слайд 33Сколько плоскостей можно провести выделенные элементы?
А) много
Б) одну
В) нисколько
7

Сколько плоскостей можно провести выделенные элементы?А) многоБ) однуВ) нисколько7

Слайд 34Если две точки прямой лежат в плоскости, то
А) прямая параллельны

плоскости
Б) прямая лежит в плоскости
В) прямая пересекает плоскость
8

Если две точки прямой лежат в плоскости, тоА) прямая параллельны плоскостиБ) прямая лежит в плоскостиВ) прямая пересекает

Слайд 35Если две точки прямой лежат в плоскости, то
А) прямая параллельны

плоскости
Б) прямая лежит в плоскости
В) прямая пересекает плоскость
8

Если две точки прямой лежат в плоскости, тоА) прямая параллельны плоскостиБ) прямая лежит в плоскостиВ) прямая пересекает

Слайд 36Если две точки прямой лежат в плоскости, то
А) прямая параллельны

плоскости
Б) прямая лежит в плоскости
В) прямая пересекает плоскость
8

Если две точки прямой лежат в плоскости, тоА) прямая параллельны плоскостиБ) прямая лежит в плоскостиВ) прямая пересекает

Слайд 37Если две точки прямой лежат в плоскости, то
А) прямая параллельны

плоскости
Б) прямая лежит в плоскости
В) прямая пересекает плоскость
8

Если две точки прямой лежат в плоскости, тоА) прямая параллельны плоскостиБ) прямая лежит в плоскостиВ) прямая пересекает

Слайд 38Если две параллельные плоскости пересечены третей, то
А) линии их пересечения

перпендикулярны

Б) линии их пересечении параллельны

В) линии их пересечения скрещиваются

9

Если две параллельные плоскости пересечены третей, тоА) линии их пересечения

Слайд 39Если две параллельные плоскости пересечены третей, то
А) линии их пересечения

перпендикулярны

Б) линии их пересечении параллельны

В) линии их пересечения скрещиваются

9

Если две параллельные плоскости пересечены третей, тоА) линии их пересечения

Слайд 40Если две параллельные плоскости пересечены третей, то
А) линии их пересечения

перпендикулярны

Б) линии их пересечении параллельны

В) линии их пересечения скрещиваются

9

Если две параллельные плоскости пересечены третей, тоА) линии их пересечения

Слайд 41Если две параллельные плоскости пересечены третей, то
А) линии их пересечения

перпендикулярны

Б) линии их пересечении параллельны

В) линии их пересечения скрещиваются

9

Если две параллельные плоскости пересечены третей, тоА) линии их пересечения

Слайд 43Построить сечение – это значит построить пересечение многогранника и плоскости
пустая

фигура
точка
отрезок
многоугольник
ά
D

Построить сечение – это значит построить пересечение многогранника и плоскостипустая фигураточкаотрезокмногоугольникάD

Слайд 44Точки тетраэдра лежат по обе стороны от плоскости
Секущая плоскость

Точки тетраэдра лежат по обе стороны от плоскостиСекущая плоскость

Слайд 45

Секущая плоскость пересекает грани


тетраэдра по отрезкам.

Секущая плоскость

Сечение

Многоугольник, сторонами которого являются эти
отрезки, есть сечение тетраэдра.

Секущая плоскость

Слайд 46Сечение многогранника
Сечение многогранника - многоугольник, вершины которого -

точки пересечения секущей плоскости с ребрами многогранника, а стороны -

линии пересечения секущей плоскости с гранями многогранника.


Сечение многогранника Сечение многогранника - многоугольник, вершины которого - точки пересечения секущей плоскости с ребрами многогранника,

Слайд 47В сечение тетраэдра –

треугольники и четырехугольники

В сечение тетраэдра – треугольники и четырехугольники

Слайд 48Сечение тетраэдра - треугольник
1

Сечение тетраэдра - треугольник1

Слайд 49Сечение тетраэдра -

четырехугольник

2

Сечение тетраэдра -

Слайд 50План построения сечений МЕТОД СЛЕДОВ
Строится линия пересечения (след) секущей плоскости с

плоскостью основания многогранника.
Используя полученные (и заданные) точки, получают следы секущей

плоскости на гранях многогранника.
Затем используя след секущей плоскости, находят точки пересечения ребер многогранника с секущей плоскостью .
Соединяем отрезки и заштриховываем сечение.
План построения сечений МЕТОД СЛЕДОВСтроится линия пересечения (след) секущей плоскости с плоскостью основания многогранника.Используя полученные (и заданные)

Слайд 51Практикум СЕЧЕНИЯ ТЕТРАЭДРА

Практикум СЕЧЕНИЯ ТЕТРАЭДРА

Слайд 52В сечение параллелепипеда –

разные многоугольники

В сечение параллелепипеда –

Слайд 53Сечение параллелепипеда -

четырехугольник
1

Сечение параллелепипеда -

Слайд 54Сечение параллелепипеда -

четырехугольник


2

Сечение параллелепипеда -

Слайд 55План построения сечений в

параллелепипеде

Соединить точки, принадлежащие одной грани многогранника.
В параллельных гранях построить линии, параллельные данным


План построения сечений в

Слайд 56Сечение параллелепипеда -

шестиугольник


3

Сечение параллелепипеда -

Слайд 57План построения сечений
Соединить точки, принадлежащие одной грани многогранника
В параллельных гранях

построить линии, параллельные данным
Построить след секущей:
продолжить рёбра основания
найти точки

пересечения ребер многогранника
с секущей плоскостью

План построения сеченийСоединить точки, принадлежащие одной грани многогранникаВ параллельных гранях построить линии, параллельные даннымПостроить след секущей: продолжить

Слайд 58Практикум СЕЧЕНИЯ ПАРАЛЛЕЛЕПИПЕДА

Практикум СЕЧЕНИЯ ПАРАЛЛЕЛЕПИПЕДА

Слайд 59ПРАВИЛА ПОСТРОЕНИЯ

СЕЧЕНИЙ
Для построения сечения достаточно построить точки пересечения секущей

плоскости с ребрами фигуры.
Через полученные точки, лежащие в одной грани, провести отрезки.
Если невозможно соединить точки, строим след секущей плоскости и получаем недостающие точки.
Многогранник, ограниченный данными отрезками, и есть построенное сечение.
Если секущая плоскость пересекает противоположные грани параллелепипеда по каким – то отрезкам, то эти отрезки – параллельны.
ПРАВИЛА ПОСТРОЕНИЯ СЕЧЕНИЙДля построения сечения достаточно

Слайд 60Выяснить, какие сечения построены неправильно
1
2
3
4
5
6
8
7
9
10

Выяснить, какие сечения построены неправильно12345687910

Слайд 61Домашнее задание
Придумайте задание для построения сечений тетраэдра и параллелепипеда и

постройте эти сечения.

Домашнее заданиеПридумайте задание для построения сечений тетраэдра и параллелепипеда и постройте эти сечения.

Похожие презентации

Многогранники Многогранники 401
Обобщающий урок по теме Признаки равенства треугольников Обобщающий урок по теме Признаки равенства треугольников 367
Виды треугольников 7 класс Виды треугольников 7 класс 316
Задачи на объём конуса Задачи на объём конуса 537
Контрольная работа по геометрии Метод координат 9 класс УМК Л.С. Атанасян Контрольная работа по геометрии Метод координат 9 класс УМК Л.С. Атанасян 530
Аксиома параллельных прямых Аксиома параллельных прямых 337
Столбчатые диаграммы 6 класс Столбчатые диаграммы 6 класс 509
Площадь. Площадь трапеции 9 класс Площадь. Площадь трапеции 9 класс 352
Задачи на повторение по геометрии 9 класс Задачи на повторение по геометрии 9 класс 516
Теорема о площади треугольника 9 класс Теорема о площади треугольника 9 класс 362
Параллелепипед Параллелепипед 574
Танграм 8 класс Танграм 8 класс 322
Векторы Векторы 336
Неевклидова геометрия Неевклидова геометрия 549
Многоугольники вокруг нас 8 класс Многоугольники вокруг нас 8 класс 336
Сложение и вычитание векторов 9 класс Сложение и вычитание векторов 9 класс 547
Цилиндр. Площадь его поверхности Цилиндр. Площадь его поверхности 409
Описанная и вписанная окружности Описанная и вписанная окружности 323
История возникновения Геометрии История возникновения Геометрии 410
Геометрический цирк Геометрический цирк 423

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика