Презентация по геометрии 8 класс "Определение подобных треугольников"

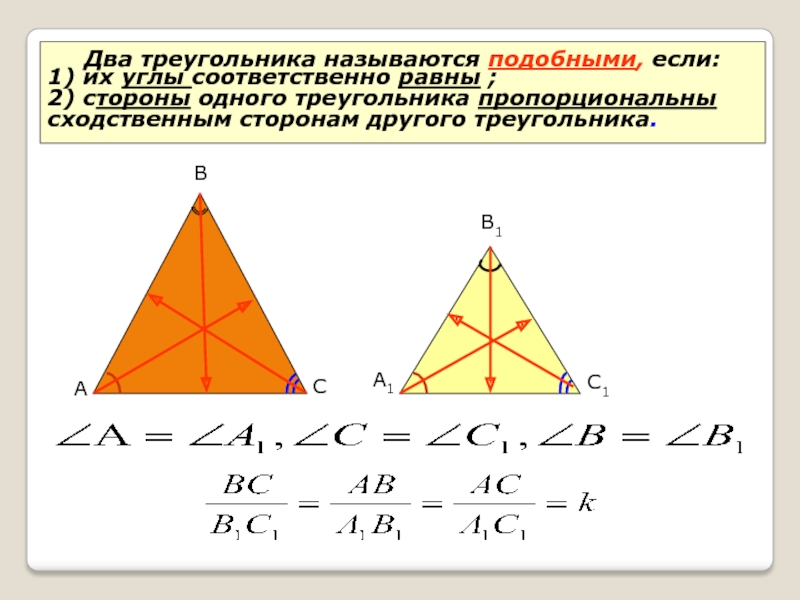
В прямоугольном треугольнике:
а=5, с=6, в=?
1. Площадь ромба
2. Площадь прямоугольного

треугольника вариант

3. Площадь прямоугольника

4. Площадь равностороннего треугольника

5. В прямоугольном треугольнике:
а=4, в=5, с=?

С1D1, если отношения их длин равны.
В1
С
D
8
C1
D1
12

стороны одного треугольника пропорциональны
сходственным сторонам другого треугольника.
А
В
С
А1
В1
С1

~ Δ А1В1С1
Стороны АВ и А1В1, ВС и В1С1, АС

и А1С1 называют сходственными.

равны?
2. Могут ли быть подобными прямоугольный и равнобедренный треугольники? Прямоугольный

и тупоугольный треугольники?

3.Могут ли быть подобными треугольник с углом 500 и треугольник с углом 1000? Треугольник с углом 450 и треугольник с углом 1350?

4*. Треугольники АВС и МNK подобны, причем А =  N,
В =  K. Назовите сторону, сходственную со стороной MN.

∠С = 65°.
Чему равны углы А1,

В1, С1?

Решить задачи устно:

б) ΔАВС ~ ΔС1А1В1, АВ = 3 см, ВС = 4 см, АС = 6 см, А1В1 = 12 см.
Вычислите В1С1 и А1С1.

160; № 543, 546, 549.
Для желающих.
1.

В трапеции АВСД (АД || ВС) АС — биссектриса угла А делит трапецию на два подобных треугольника АВС и АСД , АВ = 9 см, СД = 12 см. Найдите периметр трапеции.
2. Прямая ДЕ, параллельная стороне АС треугольника АВС, отсекает от него треугольник ДВЕ, стороны которого в четыре раза меньше сторон данного треугольника. Найдите площадь треугольника АВС, если площадь трапеции АДЕС равна 30 см2.