многоугольники, а двугранные углы при всех вершинах равны между собой.
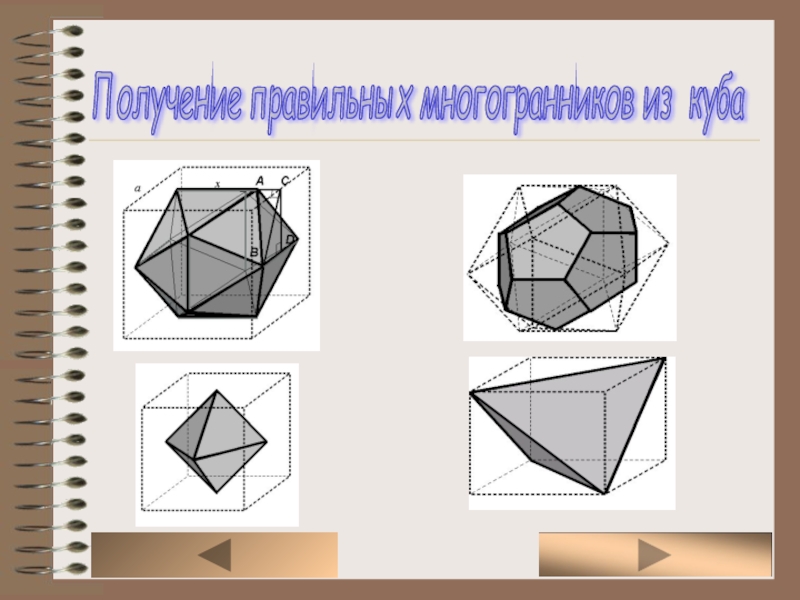
Доказано, что в каждой из вершин правильного многогранника сходится одно и то же число граней и одно и то же число ребер.Всего в природе существует пять правильных многогранников. По сравнению с количеством правильных многоугольников это – очень мало: для каждого целого n>2 существует один правильный n-угольник, т.е. правильных многоугольников – бесконечно много. Правильные многогранники имеют названия по числу граней: тетраэдр (4 грани): гексаэдр (6 граней), октаэдр (8 граней), додекаэдр (12 граней) и икосаэдр (20 граней).
Правильные и полуправильные многогранники