Сферы, описанные около многогранников

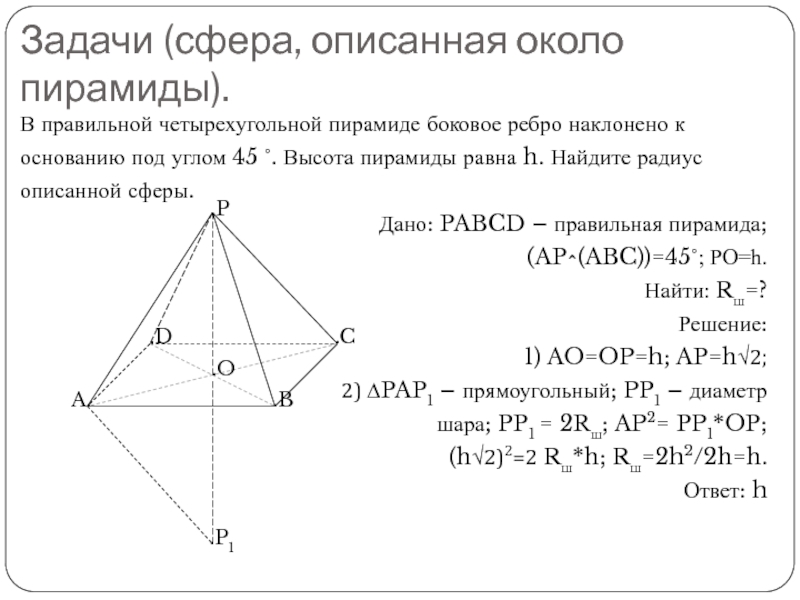
все
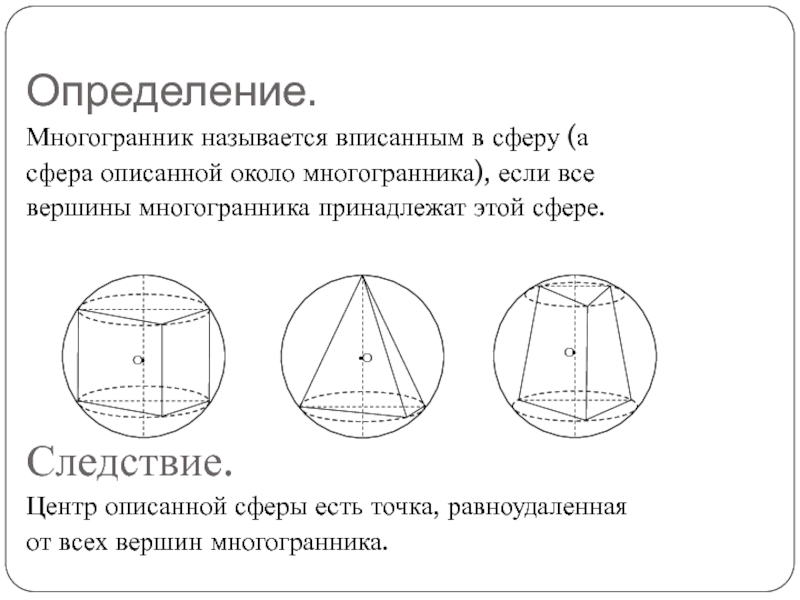
вершины многогранника принадлежат этой сфере.






Следствие.
Центр описанной сферы есть точка, равноудаленная
от

всех вершин многогранника.

.

.

.

к отрезку с
концами в данных точках, проходящая через его
середину (плоскость

серединных перпендикуляров к
этому отрезку).

AB ┴ α
AO=OB

α

A

B

O

окружности, есть прямая,
перпендикулярная плоскости этих точек, проходящая
через центр описанной около

них окружности.

C

E

A

B

D

O

a

.

.

.

.

.

.

C

E

A

B

D

.

.

.

.

.

всегда можно описать окружность.
2) Около любой правильной призмы можно описать

сферу, т.к. правильная призма является прямой и около правильного многогранника всегда можно описать окружность.

.

.

.

с катетами 6 и 8. Боковое ребро
призмы равно 24. Найдите

Радиус шара.
Дано: ∆ABC – прямоугольный;
AC=6, BC=8, AA1=24.
Найти: Rш=?
Решение:
1)OO1 ┴AB1; OO1=AA1=24.
2) ABC: AB=10.
3) OшOB: Rш=OшB=√OOш2 + OB 2 =
=√144+25=13
Ответ: 13.

О1

О

.

.

.

Rш

Ош

С1

B1

A1

A

С

B

шара.
Дано:AB=a=2; BC=b=3;
CC1=c=5.
Найти: Rш=?
Решение:
1) AC2 =a2+b2+c2.
2) A1C2 =25+9+4=38 (Свойство

диагоналей прямоугольного параллелепипеда)
3) A1C=√38; Rш= OшC= √38/2
Ответ: √38/2

D1

C1

B1

A1

A

B

C

D

5

2

3

.

.

.

Oш

равно 2a. Найдите радиус описанного
шара.
Дано: AB=BC=AC=a, AA1┴ABC;
AA1= 2a.
Найти: Rш=?
Решение:
1)AB=AO√3;

AO=a/√3.
2)Rш=√a2 + a2/3=2a/√3
Ответ: 2a/√3

C1

B

A1

C

B1

A

Oш

Rш

.

O

O1

треугольника всегда можно описать
окружность.
2)Около правильной пирамиды всегда можно описать

сферу.
3)Если боковые ребра пирамиды равны
(одинаково наклонены к основанию),
то около такой пирамиды всегда можно
описать сферу.

*В последних двух случаях центр сферы лежит на прямой, содержащей высоту пирамиды.

O

.

O

.

правильный треугольник
ABC со стороной 4√3, описан шар. Боковое ребро PA

перпендикулярно
плоскости основания пирамиды и равно 6. Найти радиус шара.
Дано: AB=BC=AC=4√3; PA┴(ABC); PA=6.
Найти: Rш=?
Решение:
1) OOСФ ┴(ABC); O – центр описанной около
∆ABC окружности; KOСФ ┴ PA; KP=AK (KOСФ
Один из серединных перпендикуляров к боковому
ребру PA); OСФ – центр описанного шара.
2) OOСФ ┴(ABC); OOСФ принадлежит (AKO);
PA┴(ABC); AK принадлежит (AKO);
значит KA||OOСФ;

.OСФ

.O

K.

P.

A.

B

.C

┴AP; AO принадлежит (AOK); значит KOcф || AO;
4) Из (2)

и (3): AOOcфK- прямоугольник, AK=PA/2=3;
5) AO=AB/√3=4;
6) ∆AOOcф: AOcф = Rш =5
Ответ: 5

наклонено к
основанию под углом 45 ˚. Высота пирамиды равна h.

Найдите радиус
описанной сферы.
Дано: PABCD – правильная пирамида;
(AP^(ABC))=45˚; PO=h.
Найти: Rш=?
Решение:
1) AO=OP=h; AP=h√2;
2) ∆PAP1 – прямоугольный; PP1 – диаметр
шара; PP1 = 2Rш; AP2= PP1*OP;
(h√2)2=2 Rш*h; Rш=2h2/2h=h.
Ответ: h

.C

.B

A.

.D

.P

.P1

.O

тетраэдра
равен R. Найдите площадь полной поверхности тетраэдра.

тетраэдр;
R – радиус сферы.
Найти: Sполн.тетр. =?
Решение:
1) Так как тетраэдр правильный,

то центр
описанной сферы принадлежит прямой,
содержащей высоту пирамиды;
2) Sполн.тетр. = a2 √3/4*4= a2√3; 3) Точки D, A, D1
принадлежат одной окружности – сечению сферы
плоскостью DAD1, значит угол DAD1 - вписанный угол, опирающийся на диаметр, DD1; угол DAD1=90˚;
4) AO – высота ∆ADD1, проведенная из вершины прямого угла. AD2= DO*DD1;
5) AO=a/√3; DO=√a2-a2/3=a√2/√3; a2=a√2/√3*2R;
a=√2/√3*2R; a2= 8R2/3;

.D1

.D

.O

.B

.C

A.

a

a

8R2 √3/3