TheSlide.ru

Педальный треугольник 10-11 класс

Содержание

1. Педальный треугольник 10-11 класс
2. СодержаниеОпределениеСвойства педального треугольникаТеоремы о педальном треугольникеЗадачи
3. Теорема 1 Теорема 2
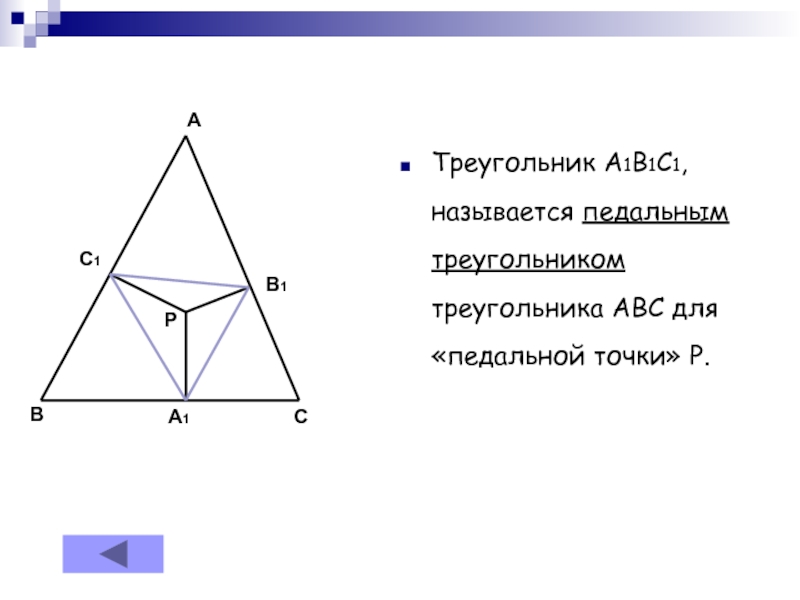
4. Треугольник A1B1C1, называется педальным треугольником треугольника ABC для «педальной точки» P.PABCA1B1C1
5. Теорема 1 Если расстояние от педальной точки до
6. PABCA1B1C1xyz
7. Теорема 2 Основания перпендикуляров, опущенных из точки на
8. Теорема 1Теорема 2Теорема 3Теорема 4. Точка Брокара
9. Теорема 1 Если из точки L внутри треугольника
10. Теорема 2 Перпендикуляры, опущенные из точки, лежащей в
11. Теорема 3Третий педальный треугольник подобен исходномуРисунок
12. ABCLcbalclalbhahbhcABLcbalclalbhahbhcSaSbSc
13. ABCOLNM
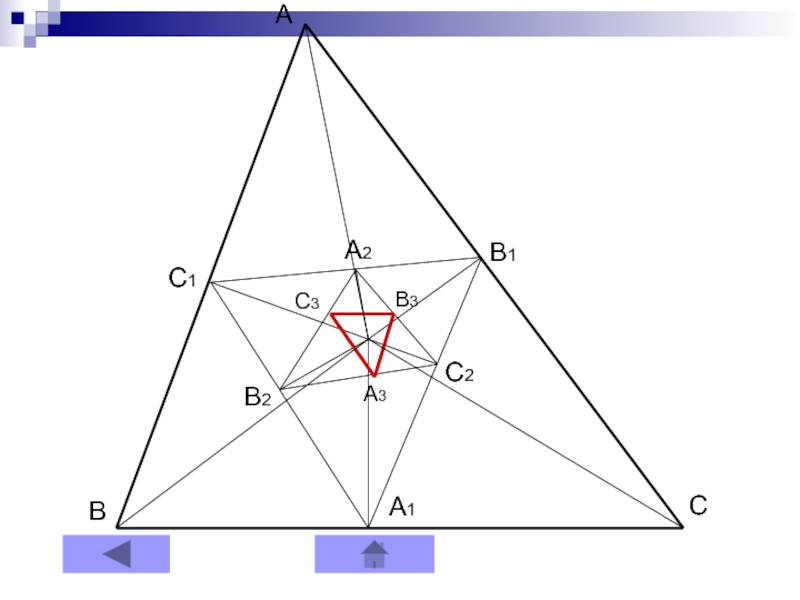
14. ABCC1B1A1A2B2C2C3A3B3
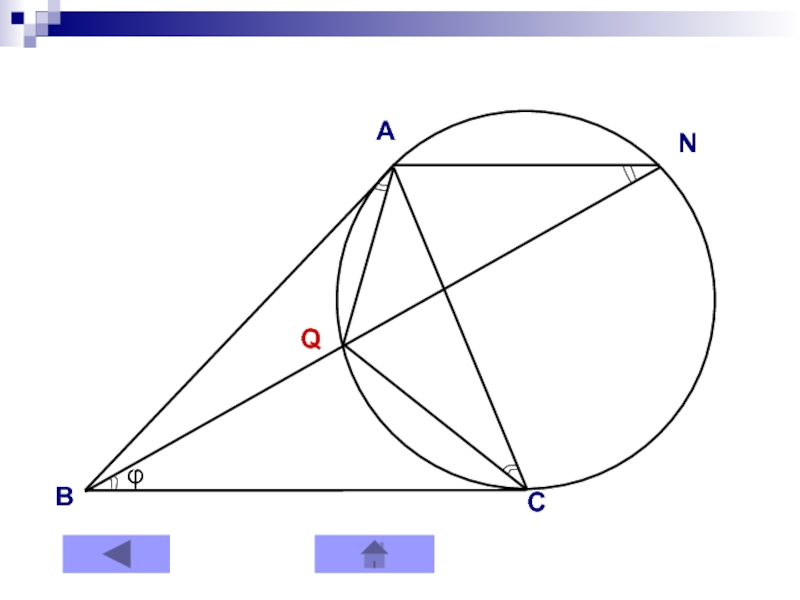
15. Теорема 4. Точка Брокара Педальный треугольник точки Брокара подобен исходному Рисунок
16. ANCBQφ
17. PCAC1BA1B1
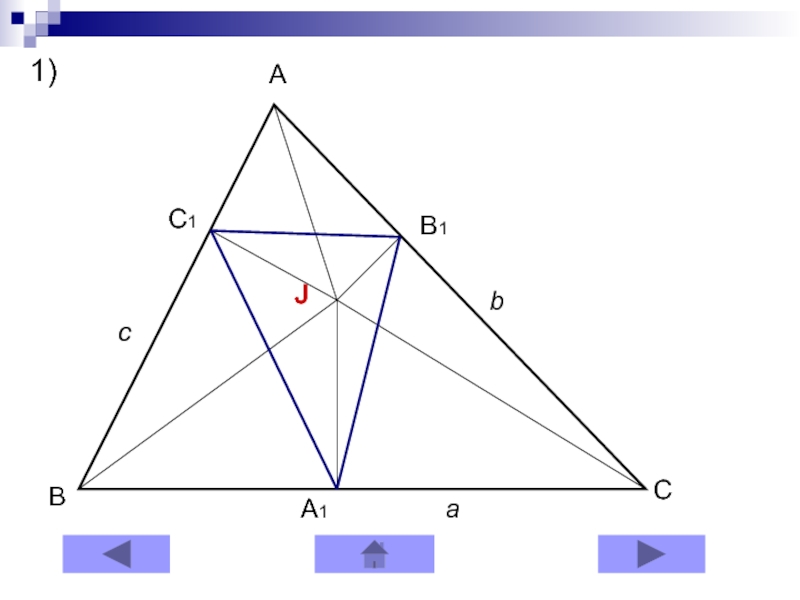
18. ABCJA1B1C1cab1)
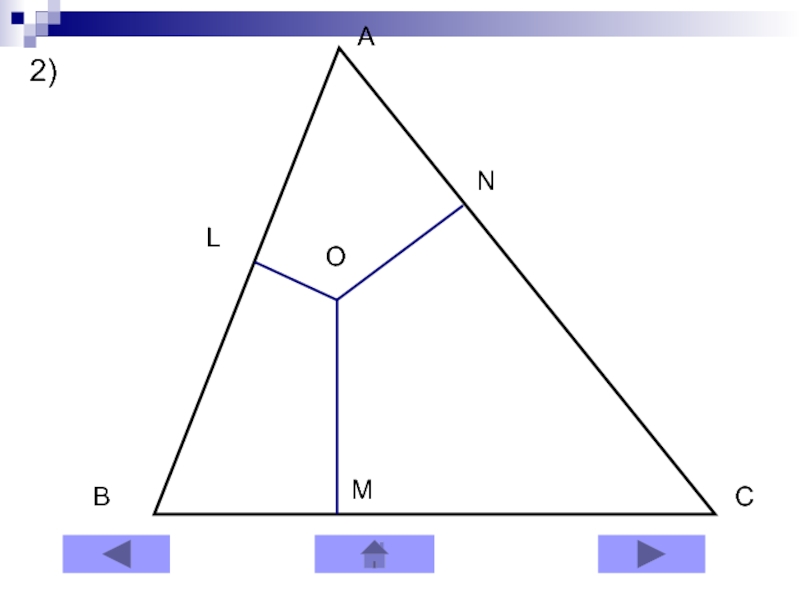
19. OABCMLN2)
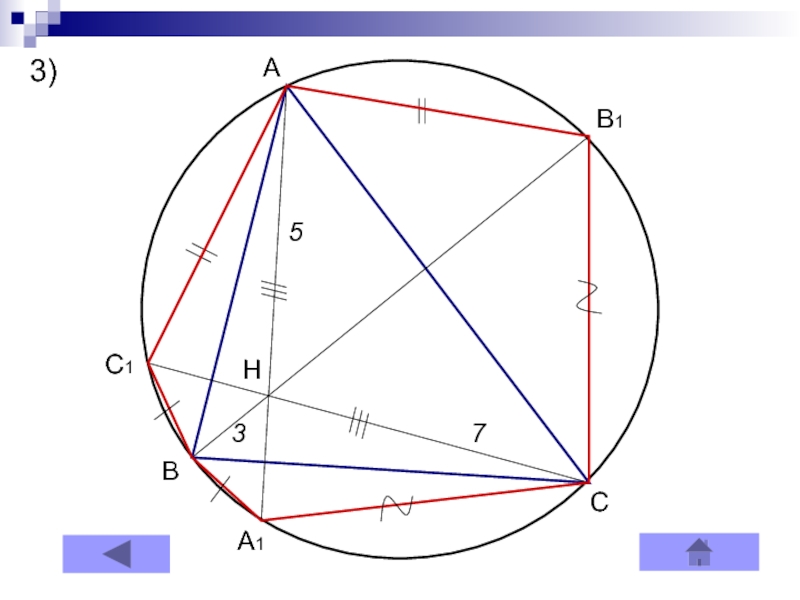
20. 3)ABCA1B1C1H573
21. Скачать презентанцию

СодержаниеОпределениеСвойства педального треугольникаТеоремы о педальном треугольникеЗадачи

Главная
Геометрия
Педальный треугольник 10-11 класс

Слайды и текст этой презентации

Слайд 1Педальный треугольник

Педальный треугольник

Слайд 2Содержание
Определение
Свойства педального треугольника
Теоремы о педальном треугольнике
Задачи

СодержаниеОпределениеСвойства педального треугольникаТеоремы о педальном треугольникеЗадачи

Слайд 3Теорема 1
Теорема 2

Теорема 1 Теорема 2

Слайд 4Треугольник A1B1C1, называется педальным треугольником треугольника ABC для «педальной точки»

P.
P
A
B
C
A1
B1
C1

Треугольник A1B1C1, называется педальным треугольником треугольника ABC для «педальной точки» P.PABCA1B1C1

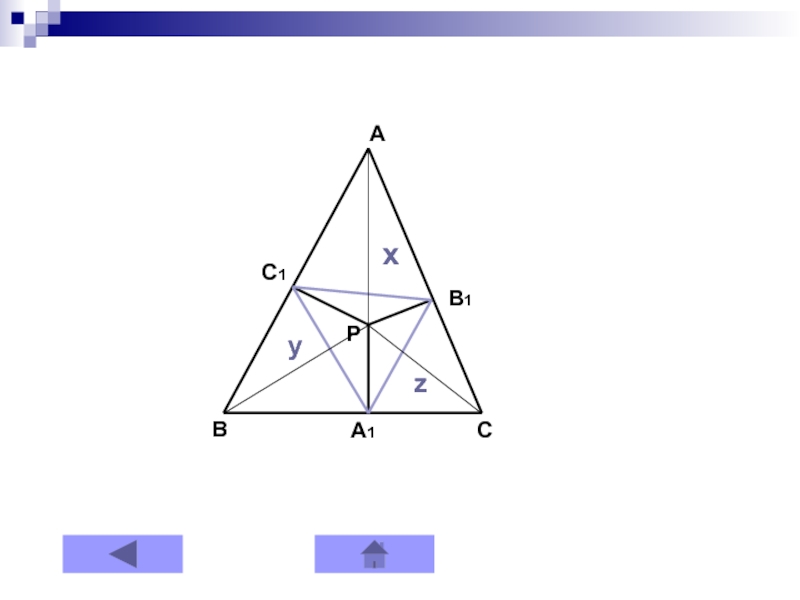
Слайд 5Теорема 1
Если расстояние от педальной точки до вершин треугольника ABC

равны x, y, z, то длины сторон треугольника равны
ax/2R,

by/2R, cz/2R, где R – радиус описанной окружности.

Рисунок

Теорема 1 Если расстояние от педальной точки до вершин треугольника ABC равны x, y, z, то длины сторон

Слайд 6P
A
B
C
A1
B1
C1

x
y
z

PABCA1B1C1xyz

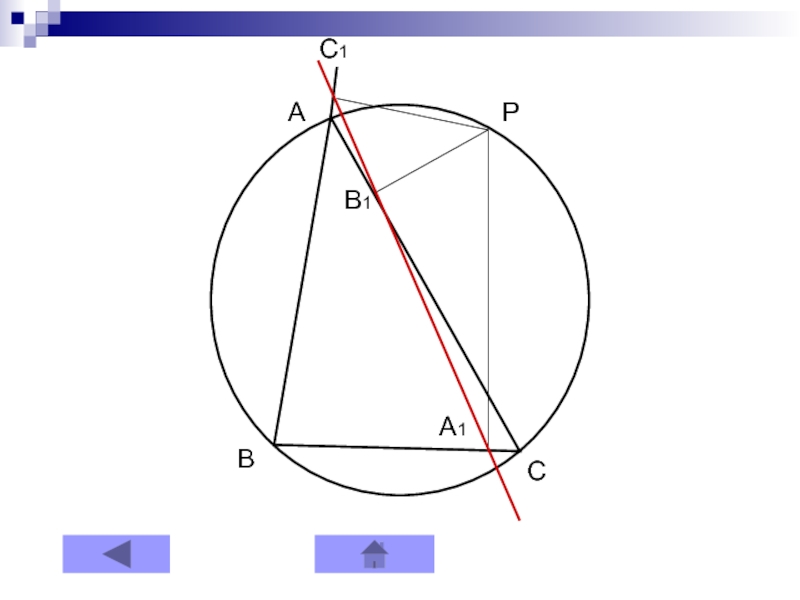
Слайд 7Теорема 2
Основания перпендикуляров, опущенных из точки на стороны треугольника, лежат

на одной прямой, тогда и только тогда, когда эта точка

лежит на описанной окружности.

Рисунок

Теорема 2 Основания перпендикуляров, опущенных из точки на стороны треугольника, лежат на одной прямой, тогда и только тогда,

Слайд 8Теорема 1
Теорема 2
Теорема 3
Теорема 4. Точка Брокара

Теорема 1Теорема 2Теорема 3Теорема 4. Точка Брокара

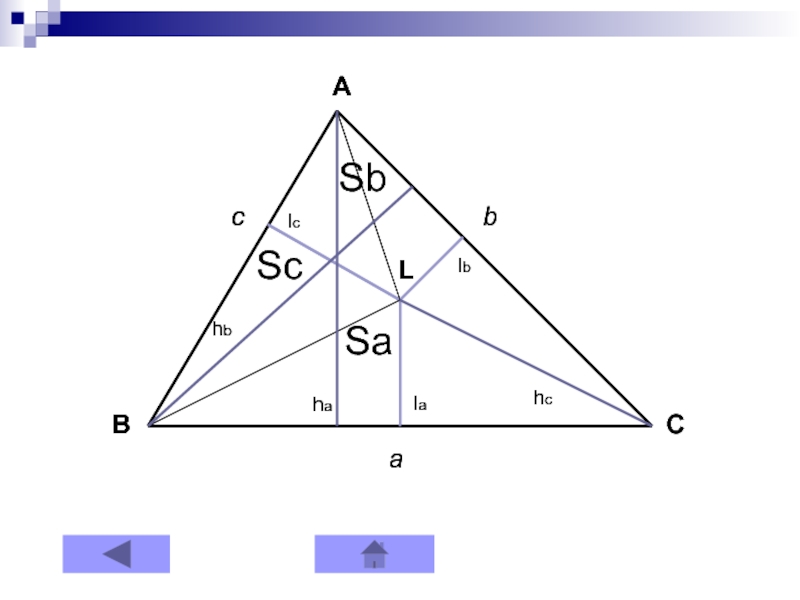
Слайд 9Теорема 1
Если из точки L внутри треугольника ABC опущены перпендикуляры

la, lb, lc соответственно на стороны a, b, c треугольника,

то

+

+

= 1

Рисунок

Теорема 1 Если из точки L внутри треугольника ABC опущены перпендикуляры la, lb, lc соответственно на стороны a,

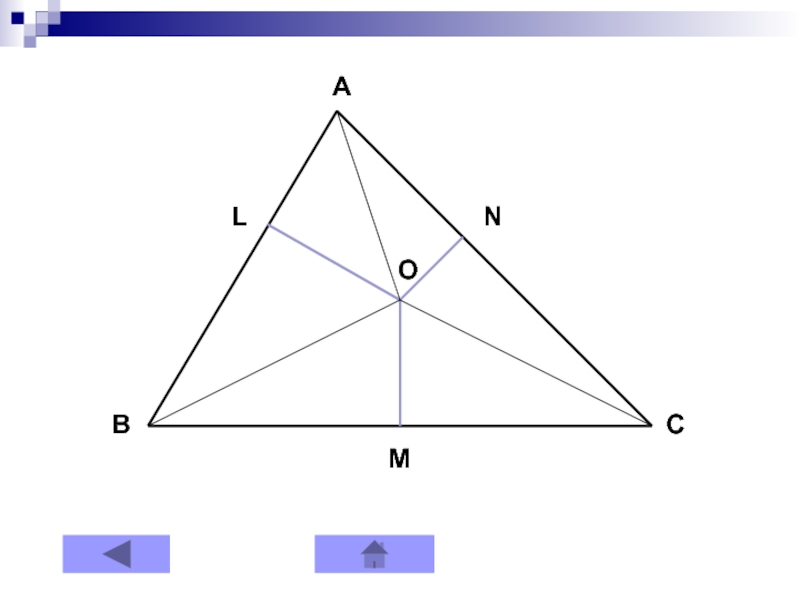
Слайд 10Теорема 2
Перпендикуляры, опущенные из точки, лежащей в плоскости треугольника, на

его стороны, определяют на сторонах шесть отрезков так, что сумма

квадратов трех отрезков, не имеющих общих концов, равна сумме квадратов трех других.

Рисунок

Теорема 2 Перпендикуляры, опущенные из точки, лежащей в плоскости треугольника, на его стороны, определяют на сторонах шесть отрезков

Слайд 11Теорема 3
Третий педальный треугольник
подобен исходному
Рисунок

Теорема 3Третий педальный треугольник подобен исходномуРисунок

Слайд 12A
B
C
L
c
b
a
lc
la
lb
ha
hb
hc

A
B
L
c
b
a
lc
la
lb
ha
hb
hc

Sa
Sb
Sc

ABCLcbalclalbhahbhcABLcbalclalbhahbhcSaSbSc

Слайд 13A
B
C
O
L
N
M

ABCOLNM

Слайд 14A
B
C
C1
B1
A1
A2
B2
C2
C3
A3
B3

ABCC1B1A1A2B2C2C3A3B3

Слайд 15Теорема 4. Точка Брокара
Педальный треугольник точки Брокара подобен исходному
Рисунок

Теорема 4. Точка Брокара Педальный треугольник точки Брокара подобен исходному Рисунок

Слайд 16

A
N
C
B
Q
φ

ANCBQφ

Слайд 17

P
C
A
C1
B
A1
B1

PCAC1BA1B1

Слайд 18
A
B
C
J
A1
B1
C1
c
a
b
1)

ABCJA1B1C1cab1)

Слайд 19
O
A
B
C
M
L
N
2)

OABCMLN2)

Слайд 203)

A
B
C
A1
B1
C1
H
5
7
3

3)ABCA1B1C1H573

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей