двух параллельных прямых к плоскости
Теорема о параллельности двух перпендикулярных прямых
к плоскостиПризнак перпендикулярности прямой и плоскости
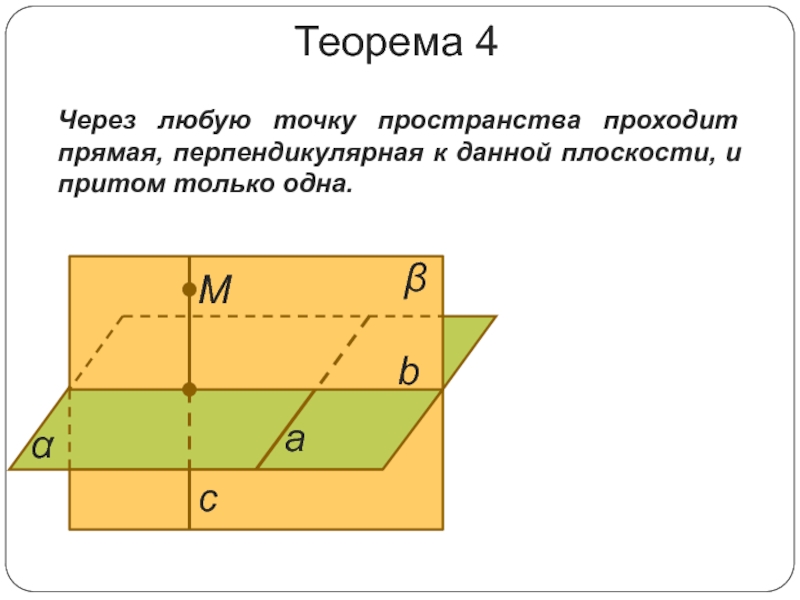
Теорема о существовании и единственности прямой, перпендикулярной к данной плоскости
Перпендикуляр и наклонные
Теорема о трех перпендикулярах
Теорема, обратная теореме о трех перпендикулярах
Угол между прямой и плоскостью