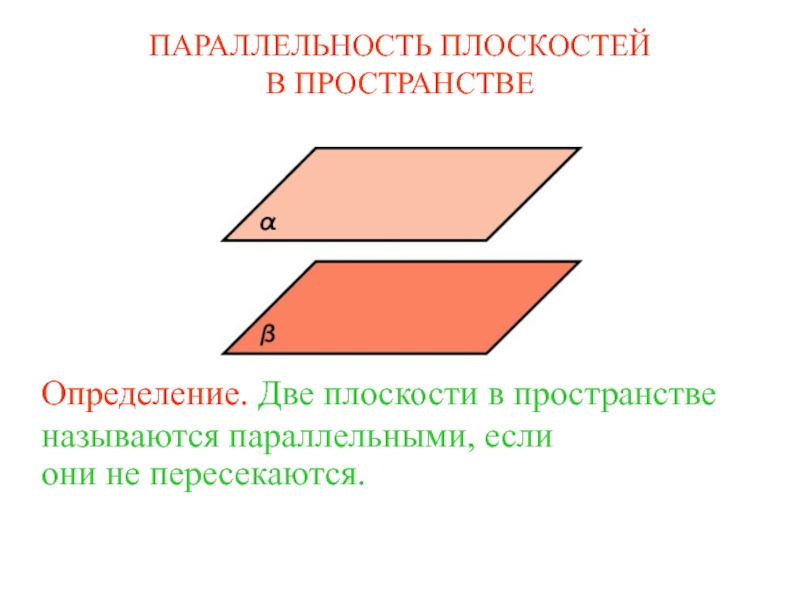
будем называть
двугранным углом
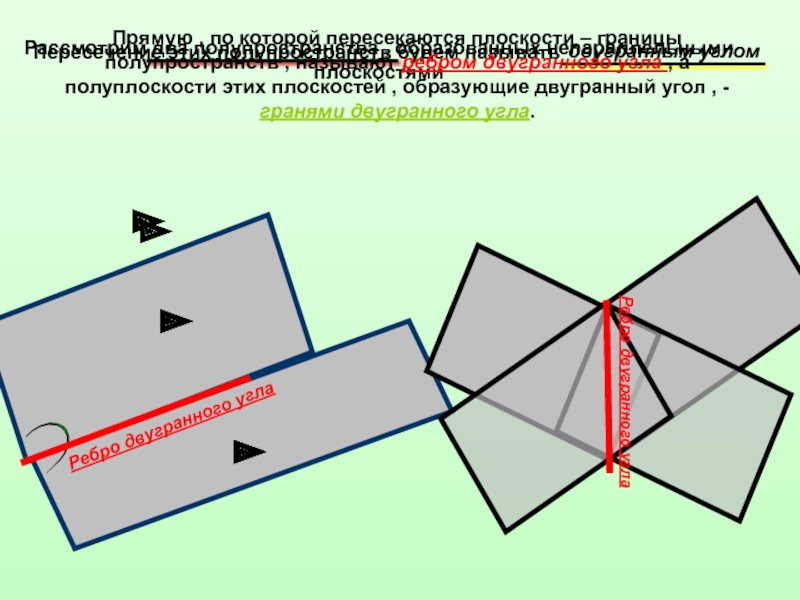
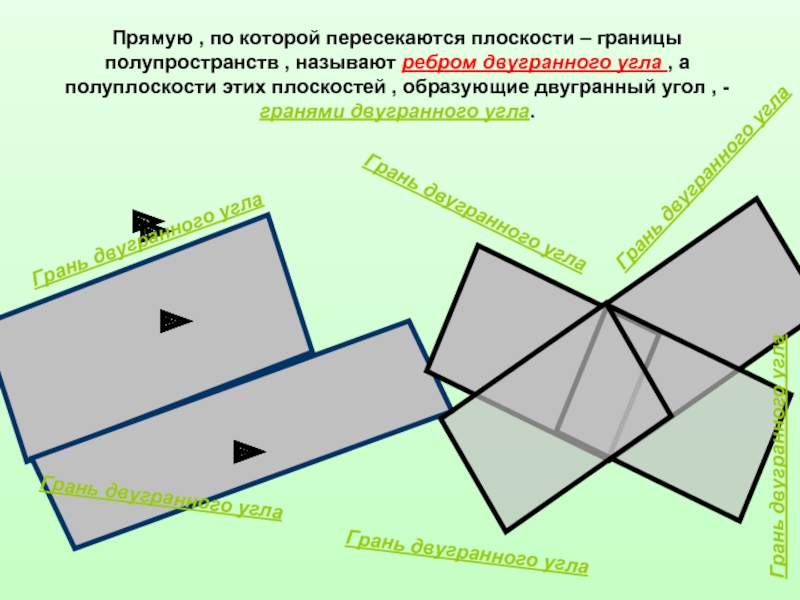
Прямую , по которой пересекаются плоскости –
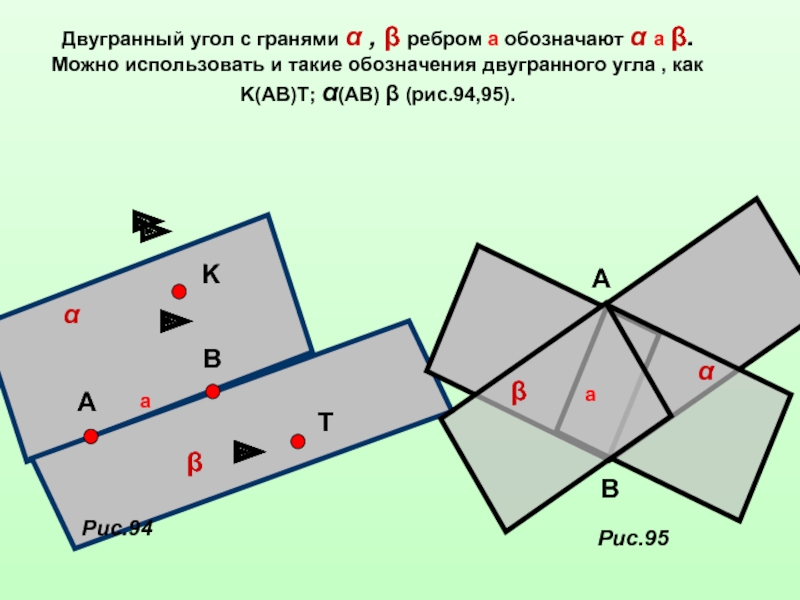
границы полупространств , называют ребром двугранного угла , а полуплоскости этих плоскостей , образующие двугранный угол , - гранями двугранного угла.Ребро двугранного угла
Ребро двугранного угла


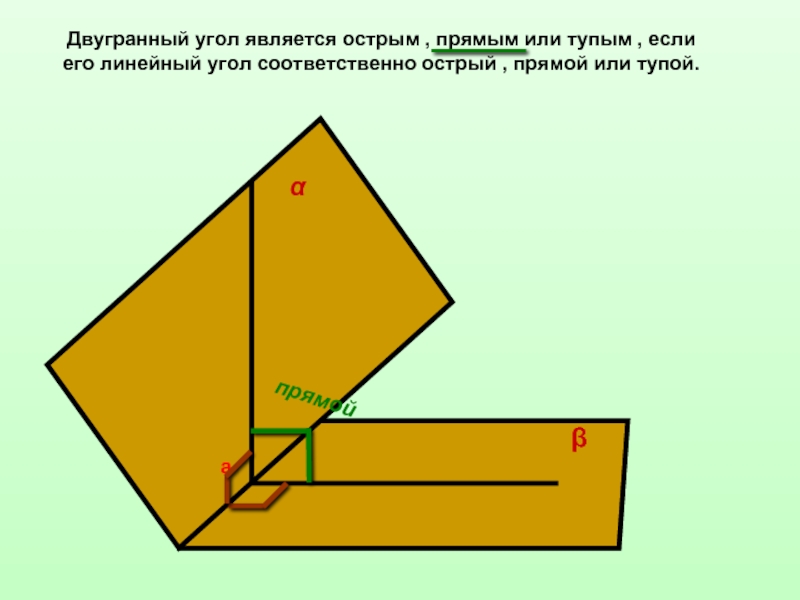
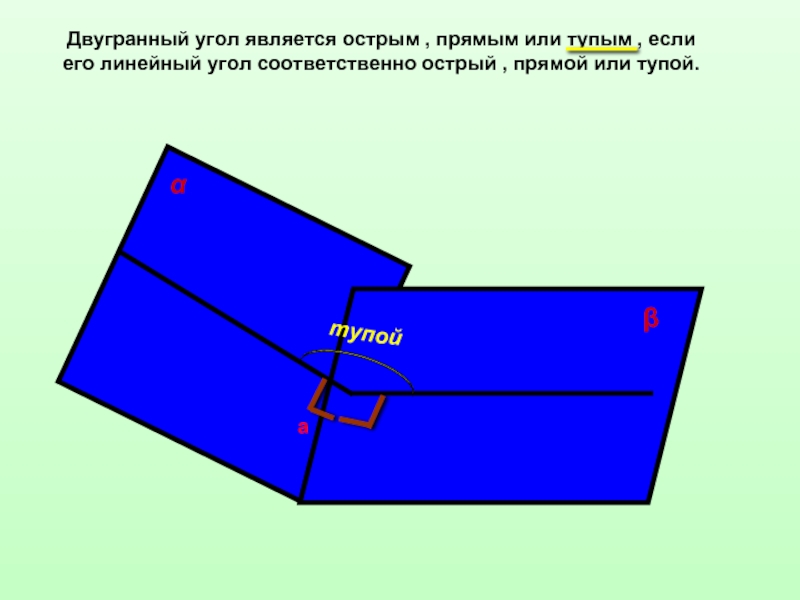
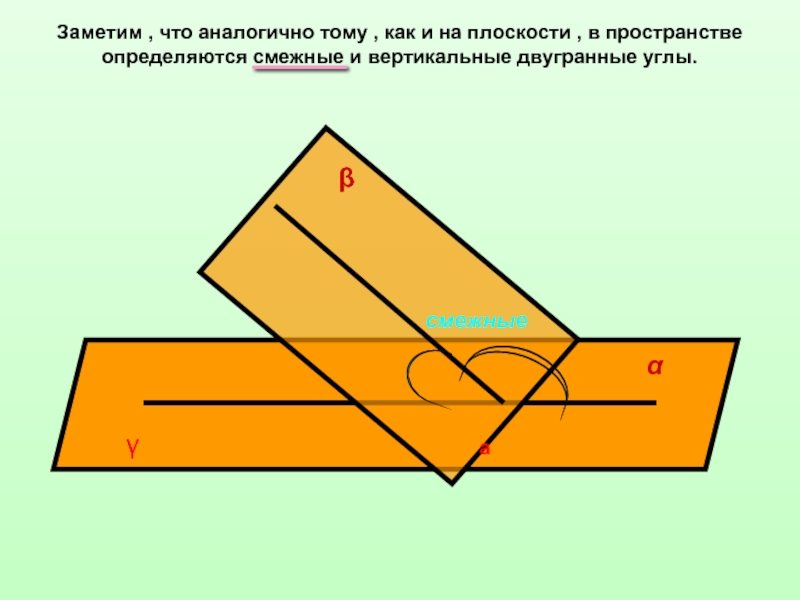
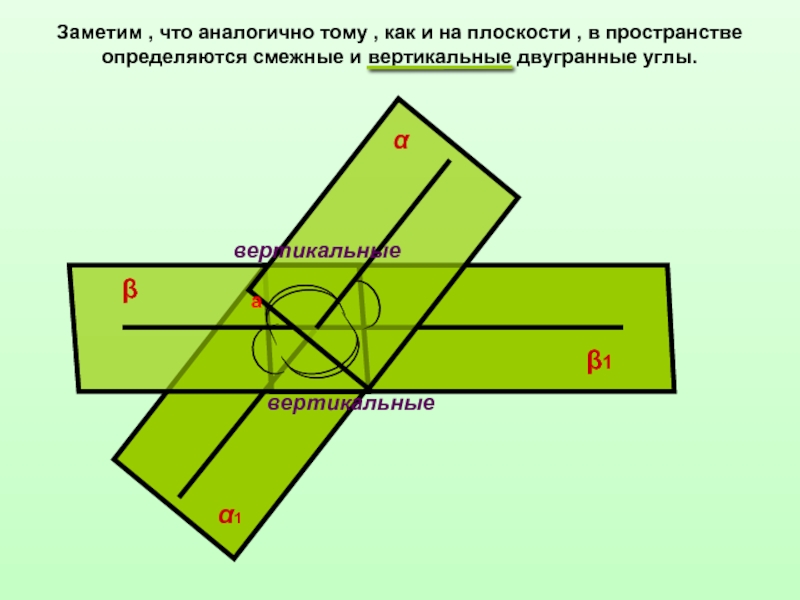

![Двугранные углы ββ1аαα1сϕВеличина угла между плоскостями принадлежит промежутку [0°;90°]. ββ1аαα1сϕВеличина угла между плоскостями принадлежит промежутку [0°;90°].](/img/thumbs/dc1658f72783ca71ac98fd6dd97c74e5-800x.jpg)