Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Трансцендентные кривые
Содержание
- 1. Трансцендентные кривые
- 2. СодержаниеКласс трансцендентных кривых Определение трансцендентной кривой Квадратриса
- 3. Большой интересный класс составляют трансцендентные кривые К
- 4. Трансцендентная кривая Трансцендентная кривая - это кривая, уравнение
- 5. Квадратриса Квадратриса (или Квадратрисса) — плоская трансцендентная кривая,
- 6. УравненияВ полярных координатах:В прямоугольных координатах можно записать уравнение квадратрисы в следующем виде:
- 7. ТрактрисаТрактриса (линия влечения) — (от лат. trahere — тащить) — плоская
- 8. Уравнения Параметрическое описание: Уравнение в декартовых координатах:
- 9. Цепная линияЦепная линия — линия, форму которой принимает
- 10. Краткая историческая справкаПоверхность, образованная вращением дуги цепной
- 11. ПрименениеАркиПеревёрнутая цепная линия — идеальная форма для арок.
- 12. ЦИКЛОИДАЦиклоида (от греч.— круглый) — плоская трансцендентная
- 13. Уравнения Примем горизонтальную ось координат в качестве
- 14. У циклоиды масса любопытнейших свойств. Оказывается, например,
- 15. Архимедова спиральАрхимедова спираль — плоская кривая, траектория
- 16. Вычисление длины дуги Архимедовой спирали Бесконечно малый
- 17. Спирали в природе и техникеСпирали в нашей
- 18. Спирали в природе и технике
- 19. Спирали в природе и технике
- 20. Спиральные галактики
- 21. Гиперболическая спираль — плоская трансцендентная кривая. Уравнение
- 22. Уравнение гиперболической спирали в декартовых координатах:Параметрическая запись
- 23. ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ - плоская трансцендентная кривая, пересекающая
- 24. Логарифмическая спираль относится к псевдоспиралям. Логарифмическая спираль
- 25. Логарифмическая спираль выполняет профиль вращающихся ножей
- 26. Клотоида или Спираль Корню — кривая, у
- 27. Описывается параметрическими уравнениями где
- 28. ТрохоидаТрохоида (от греч. τροχοειδής — колесообразный) —
- 29. Гипоциклоида Гипоциклоида (от греческих слов ὑπό — под,
- 30. ЭпициклоидаЭпициклоида (от греч. ὲπί — на, над,
- 31. УравненияЕсли центр неподвижной окружности находится в начале
- 32. ПрименениеПоследнее уравнение выражает такое кинематическое свойство эпициклоиды:
- 33. Информационные источникиЛитература1. Большой энциклопедический словарь «Математика»,Гл. редактор
- 34. Скачать презентанцию
СодержаниеКласс трансцендентных кривых Определение трансцендентной кривой Квадратриса Трактриса Цепная линия Циклоида Архимедова спираль Гиперболическая спираль Логарифмическая спираль Спираль Корню, клотоидаТрохоидаГипоциклоида Эпициклоида
Слайды и текст этой презентации
Слайд 1Федеральное государственное образовательное учреждение среднего профессионального образования «Димитровградский технический колледж»
Проект
по
теме: «Трансцендентные кривые»
Слайд 2Содержание
Класс трансцендентных кривых
Определение трансцендентной кривой
Квадратриса
Трактриса
Цепная линия
Циклоида
Архимедова спираль
Гиперболическая спираль
Логарифмическая спираль
Спираль Корню, клотоида
Трохоида
Гипоциклоида
Эпициклоида
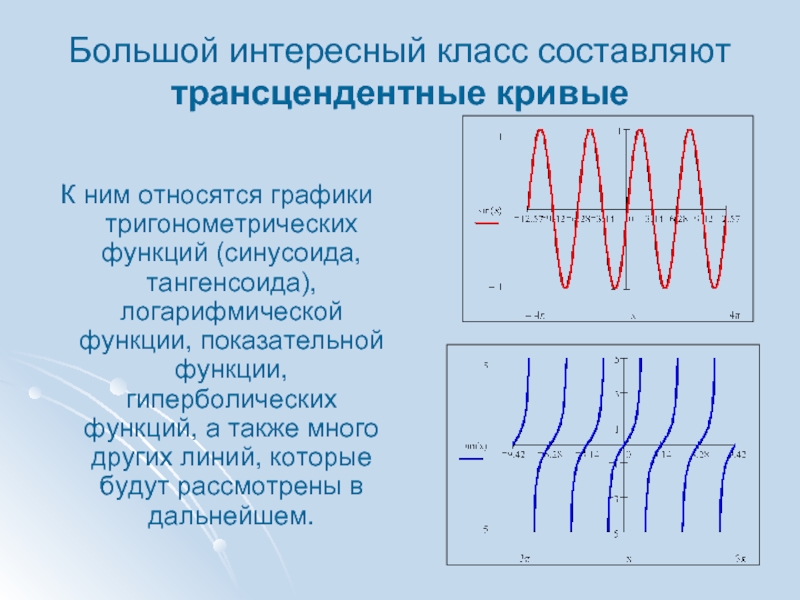
Слайд 3Большой интересный класс составляют трансцендентные кривые
К ним относятся графики
тригонометрических функций (синусоида, тангенсоида), логарифмической функции, показательной функции, гиперболических функций,
а также много других линий, которые будут рассмотрены в дальнейшем.Слайд 4Трансцендентная кривая
Трансцендентная кривая - это кривая, уравнение которой в декартовой
системе координат не является алгебраическим
( в других системах координат может
быть алгебраическим.) Логарифмическая спираль
Логарифмическая спираль
Слайд 5Квадратриса
Квадратриса (или Квадратрисса) — плоская трансцендентная кривая, определяемая кинематически.
Открыта, по сообщению Прокла Диадоха, софистом Гиппием (V век до
н. э.), использовалась в античные времена для решения задач квадратуры круга и трисекции угла.Слайд 6Уравнения
В полярных координатах:
В прямоугольных координатах можно записать уравнение квадратрисы в
следующем виде:
Слайд 7Трактриса
Трактриса (линия влечения) — (от лат. trahere — тащить) — плоская трансцендентная кривая, для
которой длина отрезка касательной от точки касания до точки пересечения
с фиксированной прямой является постоянной величиной.Такую линию описывает предмет, волочащийся на верёвке длины a за точкой, движущейся по оси абсцисс. Трактриса также является частью кривой погони при равной скорости догоняющего и убегающего.
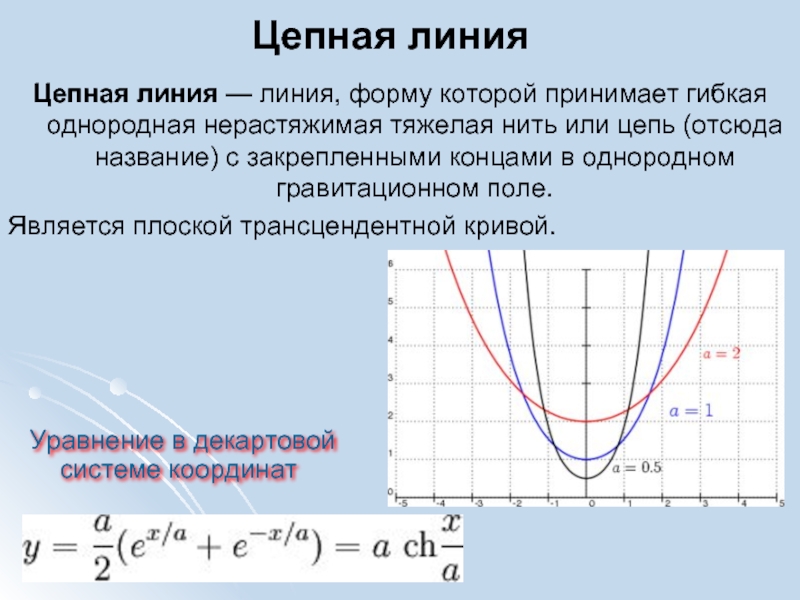
Слайд 9Цепная линия
Цепная линия — линия, форму которой принимает гибкая однородная нерастяжимая
тяжелая нить или цепь (отсюда название) с закрепленными концами в
однородном гравитационном поле.Является плоской трансцендентной кривой.
Уравнение в декартовой системе координат
Слайд 10Краткая историческая справка
Поверхность, образованная вращением дуги цепной линии вокруг оси
Оx, называется катеноидом.
Цепные линии используются в расчетах, связанных с провисанием
проводов, тросов и т.п. Форму кривой провисания впервые рассматривал Г. Галилей (1638), который считал ее параболой. Истинная форма кривой найдена Г. Лейбницем, Я. и И. Бернулли, Х. Гюйгенсом.Х. Гюйгенс предложил термин «Цепная линия»
Слайд 11Применение
Арки
Перевёрнутая цепная линия — идеальная форма для арок. Однородная арка в
форме перевёрнутой цепной линии испытывает только деформации сжатия, но не
излома.Мосты
Горбатый мост имеет форму, близкую к цепной линии.
Стоит заметить, что цепь подвесного моста имеет форму параболы, а не цепной линии. Это связано с тем, что пролёт моста намного тяжелее цепи.
Слайд 12ЦИКЛОИДА
Циклоида (от греч.— круглый) — плоская трансцендентная кривая. Циклоида определяется
кинематически как траектория фиксированной точки производящей окружности радиуса r, катящейся
без скольжения по прямой.Слайд 13Уравнения
Примем горизонтальную ось координат в качестве прямой, по которой катится
производящая окружность радиуса r.
Циклоида описывается параметрическими уравнениями:
Уравнение в
декартовых координатах: Циклоида может быть получена как решение дифференциального уравнения:
x = rt − rsint,
y = r − rcost.
Слайд 14У циклоиды масса любопытнейших свойств. Оказывается, например, что циклоида является
кривой наибыстрейшего спуска. Иначе говоря, скатываясь по снежной горке, профиль
которой выполнен в виде циклоиды, мы окажемся у основания горки быстрее, чем в случае другой формы горки. Траектория конца маятника, как и ограничивающие его боковые "щеки", представляют из себя циклоидуСлайд 15Архимедова спираль
Архимедова спираль — плоская кривая, траектория точки M (см
Рис. 1), которая равномерно движется вдоль луча OV
с
началом в O, в то время как сам луч OV равномерно вращается вокруг O. Другими словами, расстояние
ρ = OM пропорционально углу поворота φ луча OV.
Повороту луча OV на один и тот же угол соответствует одно и то же приращение ρ.
Слайд 16Вычисление длины дуги Архимедовой спирали
Бесконечно малый отрезок дуги dl равен
(см. Рис.):
,где dρ — приращение радиуса ρ, при приращении угла φ на dφ. Для бесконечно малого приращения угла dφ, справедливо:
.
Поэтому:
так как ρ = kφ и
dρ = kdφ
или
.
Длина дуги L равна интегралу от dl по dφ в пределах от 0 до φ:
.
Слайд 17Спирали в природе и технике
Спирали в нашей жизни встречаются на
каждом углу от простых вентиляторов и тисков, до паутины и
винтов моторных лодок.Слайд 21Гиперболическая спираль — плоская трансцендентная кривая.
Уравнение гиперболической спирали в
полярной системе координат является обратным для уравнения Архимедовой спирали и
записывается так:
Слайд 22Уравнение гиперболической спирали в декартовых координатах:
Параметрическая запись уравнения:
Спираль имеет
асимптоту y = a: при t стремящемся к нулю ордината
стремится к a, а абсцисса уходит в бесконечность:Слайд 23 ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ - плоская трансцендентная кривая, пересекающая все радиусы-векторы под
одним и тем же углом (рис.1). Уравнение в
полярных координатах:При a > 1 и
логарифмическая
спираль развертывается против хода
часовой стрелки, при
спираль закручивается по ходу
часовой стрелки,
стремясь к своей асимптотической
точке O.
Если a < 1, логарифмическая
спираль закручивается против хода
часовой стрелки.
Слайд 24Логарифмическая спираль относится к псевдоспиралям. Логарифмическая спираль переходит в себя
при линейных преобразованиях плоскости:
её Эволюта,
подера – также логарифмическая спираль. При стереографической проекции плоскости на сферу логарифмическая спираль переходит в локсодромию. Логарифмическая спираль широко используется в технике: Слайд 25
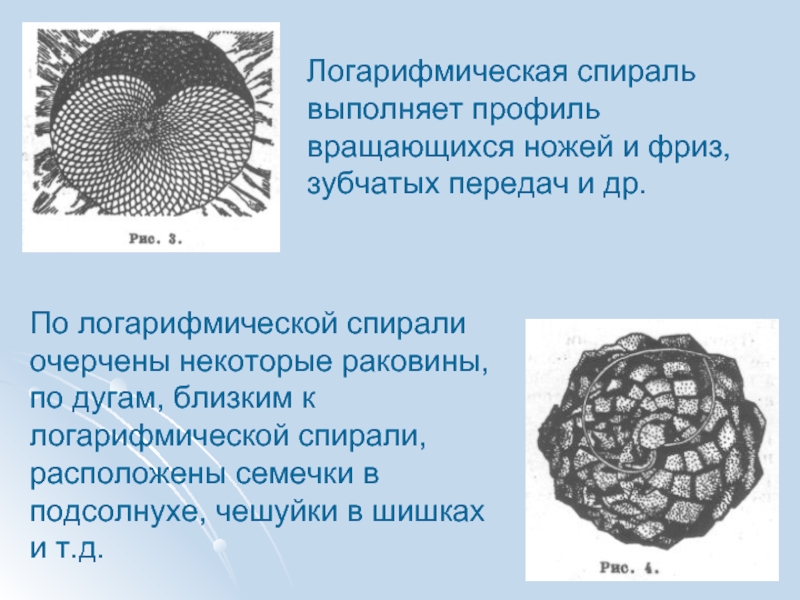
Логарифмическая спираль выполняет профиль вращающихся ножей и фриз, зубчатых
передач и др.
По логарифмической спирали очерчены некоторые раковины, по дугам,
близким к логарифмической спирали, расположены семечки в подсолнухе, чешуйки в шишках и т.д. Слайд 26Клотоида или Спираль Корню —
кривая, у которой кривизна изменяется
линейно как функция длины дуги.
Она используется как переходная дуга
в дорожном строительстве. Когда участок дороги имеет форму клотоиды, руль поворачивается равномерно. Такая форма дороги позволяет преодолевать поворот без существенного снижения скорости. Клотоида применялась Корню для облегчения расчёта дифракции в прикладных задачах.Слайд 27Описывается параметрическими уравнениями
где
, где R — радиус неподвижной окружности,
r — радиус катящейся окружности.
Модуль
величины k определяет форму гипоциклоиды. При k = 2 гипоциклоида представляет собой диаметр неподвижной окружности, при k = 4 является астроидой.Слайд 28Трохоида
Трохоида (от греч. τροχοειδής — колесообразный) — плоская трансцендентная кривая,
описываемая параметрическими уравнениями
x = rt − hsint,
y = r −
hcost.Представляет собой траекторию точки, жёстко связанной с окружностью радиуса r, катящейся без скольжения по прямой (в приведённом примере такой прямой является горизонтальная ось координат). Расстояние точки от центра окружности — h.
Если h = r трохоида переходит в циклоиду.
При h > r трохоиду называют удлинённой циклоидой, а при h < r — укороченной циклоидой.
Слайд 29Гипоциклоида
Гипоциклоида (от греческих слов ὑπό — под, внизу и κύκλος — круг,
окружность) — плоская кривая, образуемая точкой окружности, катящейся по внутренней стороне
другой окружности без скольжения.Слайд 30Эпициклоида
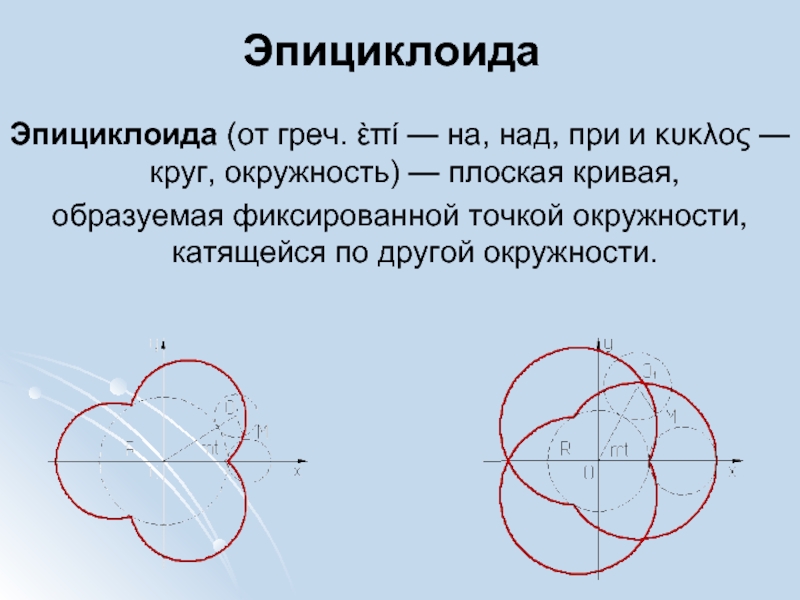
Эпициклоида (от греч. ὲπί — на, над, при и κυκλος
— круг, окружность) — плоская кривая,
образуемая фиксированной точкой окружности,
катящейся по другой окружности. Слайд 31Уравнения
Если центр неподвижной окружности находится в начале координат, её радиус
равен R, радиус катящейся по ней окружности равен r, то
эпициклоида описывается параметрическими уравнениями относительно :где α — угол поворота эпициклоиды относительно центра неподвижной окружности, — параметр, но фактически это угол наклона отрезка между центрами к оси OX.
Можно ввести величину , тогда уравнения предстанут в
виде
Слайд 32Применение
Последнее уравнение выражает такое кинематическое свойство эпициклоиды: если дуга обычной
эпициклоиды перекатывается без скольжения по прямой, то центр кривизны точки
касания двигается по эллипсу; центр эллипса лежит в той точке прямой, через которую перекатывается вершина эпициклоиды.Слайд 33Информационные источники
Литература
1. Большой энциклопедический словарь «Математика»,
Гл. редактор Ю.В. Прохоров, Научное
изд-во «Большая Российская Энциклопедия», М.: 1998
2. Д.В. Клетеник Сборник задач
по аналитической геометрии под ред. проф. Н.В.Ефимова, Государственное изд-во физико-математической литературы, М.: 19603. Математическая энциклопедия. Главный редактор И.М. Виноградов, т.3 – М.: «Советская энциклопедия», 1982
Интернет ресурсы:
www.college.ru
www.gee.ru
Теги