Слайд 2Изучить теорему.
Знать её применение.
Уметь решать задачи на изученную теорему.
Задачи:
Слайд 3
В курсе геометрии 7-х –9-х классов были рассмотрены важные
и интересные свойства геометрических фигур на плоскости. Но многие удивительные
соотношения и изящные геометрические факты не вошли в основной курс.
Из школьного курса нам известны теоремы о замечательных точках в треугольнике: три биссектрисы (медианы, высоты) пересекаются в одной точке. Эти свойства являются следствиями теоремы Менелая.
Введение
Слайд 4Биография ученого
Менела́й Александри́йский — древнегреческий математик и астроном, создатель системы
геометрии и тригонометрии на сфере – первой неевклидовой геометрии. Время
его жизни и деятельности определяется приведёнными в «Алмагесте» Птолемея двумя астрономическими наблюдениями, которые Менелай произвёл в Риме в первом году царствования Траяна, то есть в 98 году н. э.
Его работы: главным сочинением Меналая является «Сферика» в трёх книгах, сочинения «О вычислении хорд» в 6 книгах, «Начала геометрии» в 3 книгах, «Книга о треугольнике», «Книга о заходах знаков зодиака», «Книга о подразделении составных тел», посвящённая определению удельных весов тел, книга по гидростатике.
Слайд 5Труд «Сферика» стал вершиной достижений греков в сферической геометрии. Менелай
первым ввел в геометрический обиход и исследовал простейший сферический многоугольник
– треугольник. Он перенес на сферу евклидову теорию плоских треугольников и в числе прочего получил условие, при котором три точки на сторонах сферического треугольника или их продолжениях лежат на одной прямой. Интересно, что соответствующая теорема для плоскости в то время была уже широко известна, однако в историю геометрии она вошла именно как теорема Менелая.
Биография ученого
Слайд 6Самым замечательным считается обыкновенная теорема Менелая Александрийского, которая прежде называлась
правилом шести количеств. Содержание ее состоит в следующем. Если все
стороны треугольника пересечь прямой, то произведение их трех отрезков, из числа не имеющих общих концов, равно произведению таких же трех остальных отрезков. Менелай выражал свою теорему в виде пропорции a1:b1=b2b3:a2a3, в которой буквы a1, a2 и а3 и, соответственно, буквы b1, b2 и b3 обозначают не имеющие общих концов отрезки трех сторон треугольника. Словесным выражением этой пропорции было предложение: а1 находится к b1 в таком же сложном отношении, в каком находятся b2 к а2 и b3 к a3.
Биография ученого
Слайд 7Пусть на сторонах AB, BC и продолжении стороны AC треугольника
ABC взяты соответственно точки C1, A1, B1. Точки A1, B1,
C1 лежат на одной прямой тогда и только тогда, когда выполняется равенство:
Теорема Менелая
Слайд 8Доказательство. Предположим, что точки A1,B1, C1 принадлежат одной прямой a.Через
вершину C треугольника ABC проведем прямую, параллельную a и обозначим
через D точку её пересечения с AB. Из подобия треугольников ADC и AC1B1 следует выполнимость равенства:
Аналогично, из подобия треугольников BDC и BC1A1 следует выполнимость равенства:
Теорема Менелая
Перемножая эти равенства, получим равенство:
из которого следует требуемое равенство.
Слайд 9Докажем обратное. Пусть на сторонах AB, BC и продолжении стороны
AC треугольника ABC взяты соответственно точки С1, А1, В1, для
которых выполняется равенство .
Предположим, что прямая A1B1 пересекает прямую AB в некоторой точке С`. По доказанному, выполняется равенство:
Учитывая первое равенство, получаем равенство : , из которого следует совпадение точек C`и C1 и, значит, точки A1, B1, C1 принадлежат одной прямой.
Теорема Менелая
Слайд 10Теорема Менелая
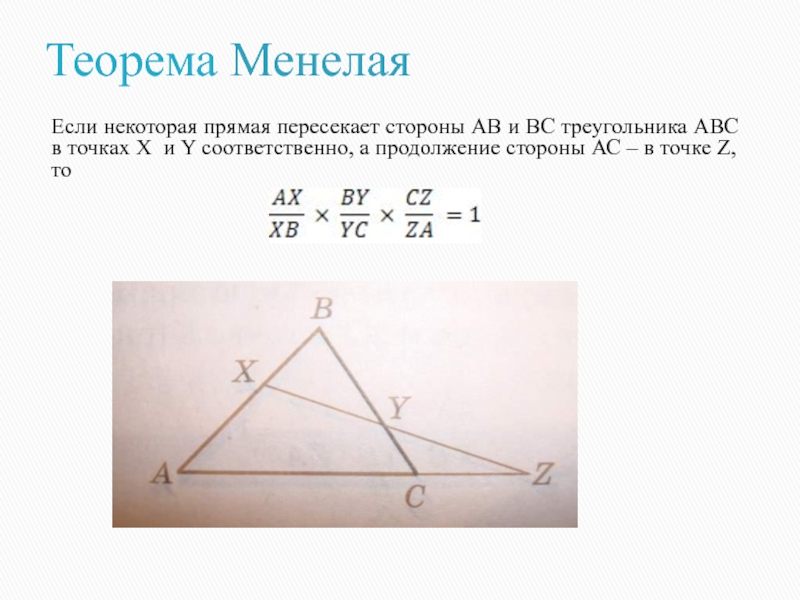
Если некоторая прямая пересекает стороны АВ и ВС треугольника
АВС в точках X и Y соответственно, а продолжение стороны
АС – в точке Z, то
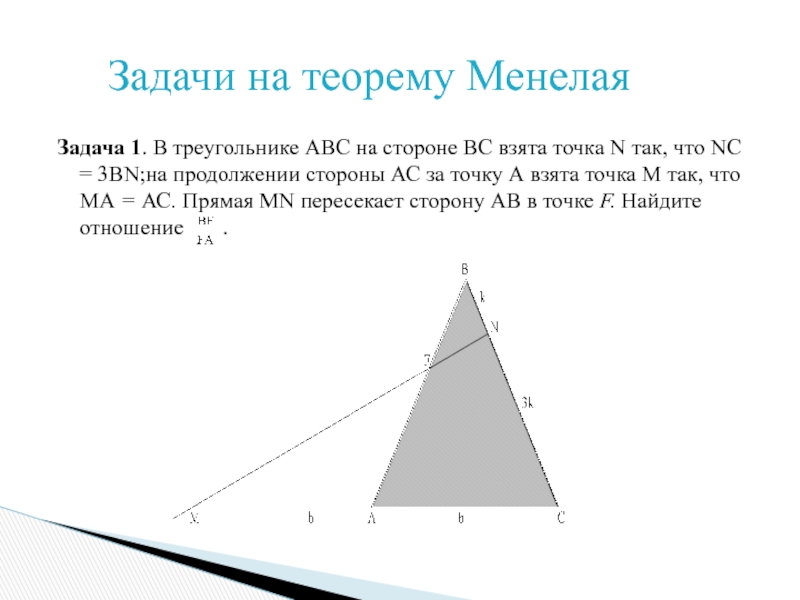
Слайд 11Задача 1. В треугольнике АВС на стороне ВС взята точка
N так, что NC = 3BN;на продолжении стороны АС за
точку А взята точка М так, что МА = АС. Прямая MN пересекает сторону АВ в точке F. Найдите отношение .
Задачи на теорему Менелая
Слайд 12Решение. По условию задачи МА = AC, NC =3BN. Пусть
МА = АС = b, BN =k, NC = 3k.
Прямая MN пересекает две стороны треугольника АВС и продолжение третьей. По теореме Менелая:
Ответ: 2 : 3.
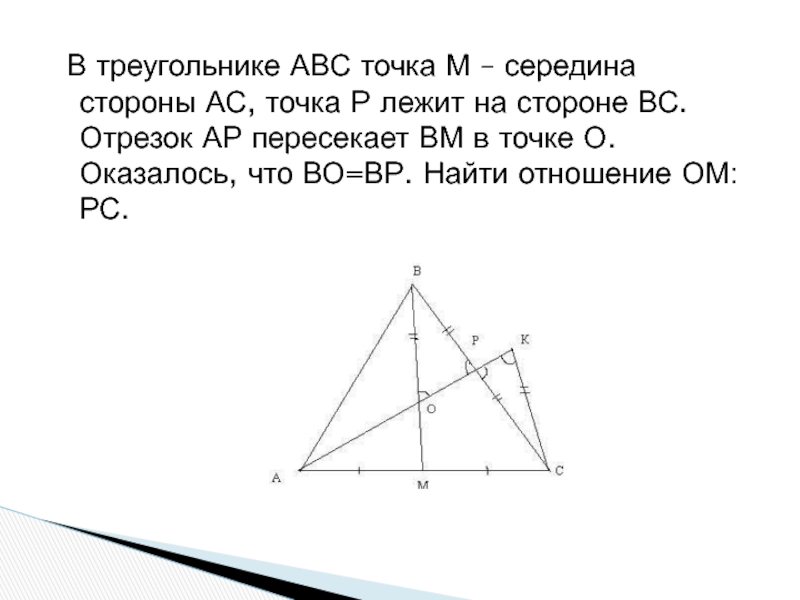
Слайд 13 В треугольнике АВС точка М – середина стороны АС,
точка Р лежит на стороне ВС. Отрезок АР пересекает ВМ
в точке О. Оказалось, что ВО=ВР. Найти отношение ОМ:РС.
Слайд 141 способ. Сделаем дополнительное построение: проведем через точку С прямую,
параллельную ВМ; точку пересечения этой прямой с прямой АР обозначим
через К.
Рассмотрим треугольники ОВР и КСР. Углы ОРВ и КРС равны как вертикальные, углы ВОР и СКР равны как накрест лежащие при пересечении параллельных прямых ВМ и СК секущей АК. Поскольку по условию треугольник ОВР равнобедренный, угол ВОР = углу ОРВ, значит, и угол СРК= углу СКР. Значит, треугольник СКР – равнобедренный, т.е. СР=КС. Но, (например, по т. Фалеса) ОМ – средняя линия треугольника САК, она в 2 раза меньше, чем СК. Получаем, что ОМ:РС = ОМ:СК = 1:2
2 способ. По т. Менелая для треугольника МВС и прямой АР выполняется равенство:
Тогда, используя условия АМ=МС и ВО=ВР
получим, что МО:РС=1:2.
Ответ: 1:2.
Слайд 15Задача 2. Пусть AD — медиана треугольника АВС. На стороне
AD взята точка К так, что АК : KD =
3:1. Прямая ВК разбивает треугольник АВС на два. Найдите отношение площадей этих треугольников.
Слайд 16Решение. Пусть AD = DC = a, KD = т;
тогда АК = 3т. Пусть Р — точка пересечения прямой
ВК со стороной АС. Необходимо найти отношение . Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то
По теореме Менелая для треугольника ADC и секущей РВ имеем:
Итак,
Ответ: 3:2.
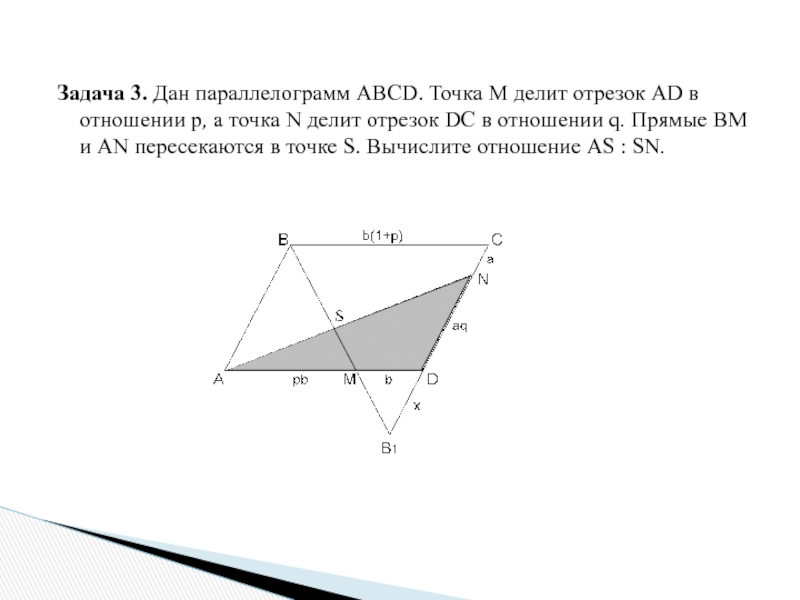
Слайд 17Задача 3. Дан параллелограмм ABCD. Точка M делит отрезок AD
в отношении р, а точка N делит отрезок DC в
отношении q. Прямые ВМ и AN пересекаются в точке S. Вычислите отношение AS : SN.
если MD = b, то AM = pb;
если NC = a, то ND = aq.
Пусть В1 – точка пересечения прямых ВМ и CD. ~ , тогда
Прямая ВВ1 пересекает две стороны и продолжение третьей треугольника AND. По теореме Менелая:
Откуда
Ответ:
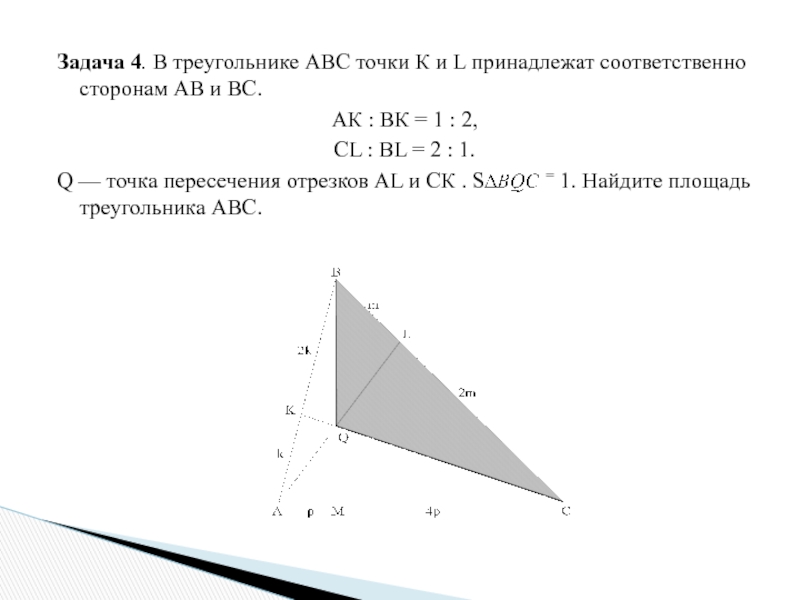
Слайд 19Задача 4. В треугольнике АВС точки К и L принадлежат
соответственно сторонам АВ и ВС.
АК : ВК = 1
: 2,
CL : BL = 2 : 1.
Q — точка пересечения отрезков AL и СК . S = 1. Найдите площадь треугольника АВС.
Слайд 20Решение.1) В треугольнике МВС прямая AL пересекает две стороны и
продолжение третьей стороны. По теореме Менелая:
(1)
В треугольнике АВМ прямая КС пересекает две стороны треугольника и продолжение третьей стороны. По теореме Менелая:
(2)
то есть MC = 4.p, AM = p.
2) Еще раз перепишем равенство (1):
то есть
3) Треугольники BQC и МВС имеют общий угол, значит,
Тогда = .
Слайд 214) Треугольники АВС и МВС имеют равные высоты, проведенные из
вершины В, значит,
=
=
Ответ: 1,75.
Слайд 22Задача 5.
Дано: окружность S касается окружностей S1 и S2 в
точках А1 и А2.
Доказать: что прямая А1А2 проходит через точку
пересечения общих внутренних или внешних касательных к окружностям S1 и S2.
S1
S2
A2
A1
S
Слайд 23Доказательство.
Пусть О, О1 и О2 – центры
окружностей S, S1
и S2; X – точка
пересечения прямых О1О2 и А1А2.
Применяя теорему
Менелая к
треугольнику ОО1О2 и точкам А1,
А2 и Х, получаем:
а значит, О1Х : О2Х = R1 : R2, где
R1 и R2 – радиусы окружностей
S1 и S2. Следовательно, Х – точка
пересечения общих внешних или внутренних
касательных к окружностям S1 и S2.
X
S
A1
A2
O1
O2
S1
S2
О
Слайд 24Задача 6. На стороне PQ треугольника PQR взята точка N,
а на стороне РR — точка L, причем NQ =
LR. Точка пересечения отрезков QL и NR делит QL в отношении т : п , считая от точки Q. Найдите
Слайд 25Решение. По условию NQ=LR ,
Пусть NA = LR = а, QF =
km, LF = kn. Прямая NR пересекает две стороны треугольника PQL и продолжение третьей. По теореме Менелая:
Ответ: n : m.
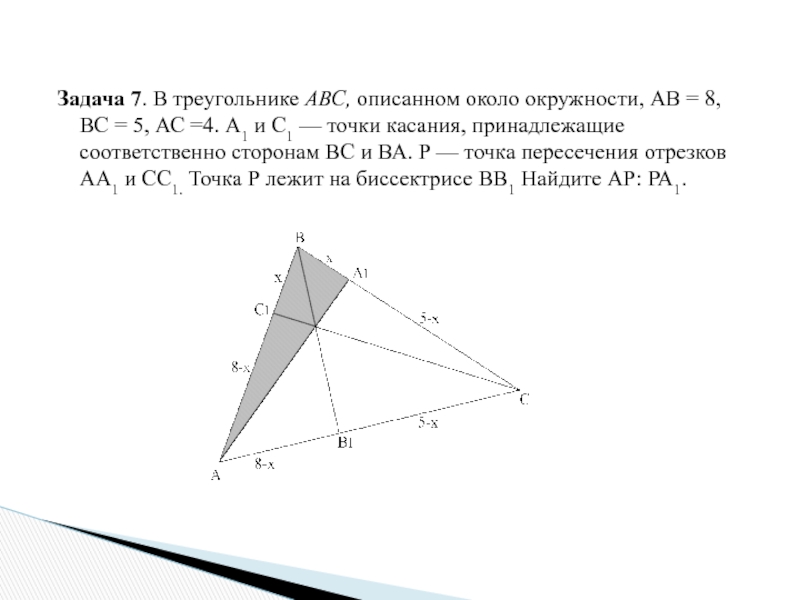
Слайд 26Задача 7. В треугольнике АВС, описанном около окружности, АВ =
8, ВС = 5, АС =4. А1 и С1 —
точки касания, принадлежащие соответственно сторонам ВС и ВА. Р — точка пересечения отрезков АА1 и СС1. Точка Р лежит на биссектрисе ВВ1 Найдите АР: РА1.
Слайд 27Решение. Точка касания окружности со стороной АС не совпадает с
В1, так как треугольник АВС — разносторонний. Пусть С1В =
х , тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (см. рисунок)
8- x + 5 – x = 4, x
Значит,
В треугольнике АВА1, прямая С1С пересекает две его стороны и продолжение третьей стороны. По теореме Менелая:
Ответ: 70 : 9.
Слайд 28Задача 8. В треугольник АВС, описанном около окружности, АВ =
8, ВС = 12, АС = 9, А1 и С1
— точки касания, лежащие соответственно на сторонах ВС и АВ. Q — точка пересечения отрезков АА1 и ВВ1. Q лежит на высоте ВВ1. Найдите отношение BQ : QB1
Слайд 29Решение. Треугольник АВС — разносторонний, значит, точка В1 не совпадает
с точкой касания.
1) Пусть С1В = х, тогда, используя свойство
касательных, проведенных к окружности из одной точки, введем обозначения (см. рисунок):
(13 – х) + (12 – х) = 9, х = 8.
Значит, С1В = 8, АС1 = 5.
2) По формуле Герона: S =
S =
3) Из треугольника ABB1 (прямоугольного) по теореме Пифагора :
4) В треугольнике ABB1 прямая CC1 пересекает две его стороны и продолжение третьей. По теореме Менелая:
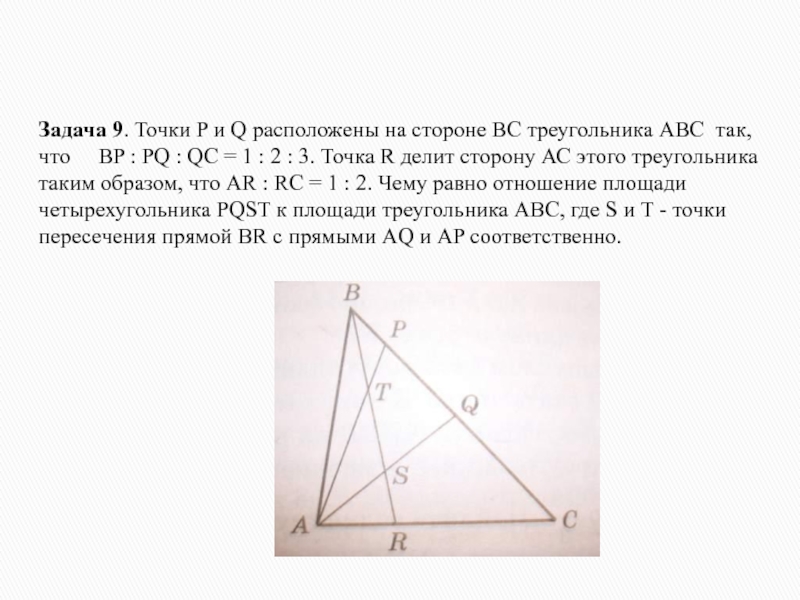
Слайд 31Задача 9. Точки P и Q расположены на стороне ВС
треугольника АВС так, что BP : PQ :
QC = 1 : 2 : 3. Точка R делит сторону АС этого треугольника таким образом, что AR : RC = 1 : 2. Чему равно отношение площади четырехугольника PQST к площади треугольника АВС, где S и T - точки пересечения прямой ВR с прямыми АQ и АP соответственно.
Слайд 32Решение. Обозначим BP = x, AR = y; тогда PQ
= 2x, QC = 3x, RC = 2y. Вычислим, какую
часть площадь четырехугольника PQST составляет от площади треугольника APQ, а значит, и от площади треугольника ABC. Для этого нам понадобятся отношения, в которых точки S и T делят прямые AQ и AP соответственно. Применим к треугольнику ACQ и секущей SR теорему Менелая:
Аналогично, применив теорему Менелая к треугольнику ACP и секущей TR, получим:
Далее:
Слайд 33C другой стороны, применив лемму о площадях к треугольникам APQ
и ABC, получим, что
Ответ: .
Слайд 34Задача 10. В треугольнике АВС длина высоты ВD равна 6,
длина медианы СE равна 5, расстояние от точки пересечения ВD
с СE до стороны АС равно 1. Найти длину стороны АВ.
Слайд 35Решение. Пусть точка О – точка пересечения прямых BD и
CE. Расстояние от точки О до середины AC(равное по условию
единице) есть длина отрезка OD. Итак, OD = 1 и OB = 5. Применим к треугольнику ABD и секущей OE теорему Менелая:
Применив теперь теорему Менелая к треугольнику ACE и секущей OD, получим, что
откуда OE = 2CO, и с учетом OE + CO = CE = 5 получаем, что CO = . К прямоугольному треугольнику COD применим теорему Пифагора:
Значит, AD = 4CD = . Наконец, рассмотрим прямоугольный треугольник ABD, в нем также воспользуемся теоремой Пифагора:
Ответ: .
Слайд 36В треугольнике АВС отрезки АД и ВМ, проведенные из вершин
А и В соответственно к сторонам ВС и ФС, пересекаясь
в точке Р, делятся в отношении АР:РД =3:2 и ВР:РМ=4:5. В каком отношении точки Д и М делят стороны треугольника, считая от С?
В треугольнике АВС точка Д делит сторону ВС в отношении ВД:ДС=3:4. Точка М делит сторону АС в отношении АМ:МС=2:5. Отрезки АД и ВМ пересекаются в точке К. Найдите площадь треугольника АКМ, если площадь треугольника ВКД равна 45.
В треугольнике АВС точка К делит сторону АВ в отношении АК:КВ=1:2, а точка Р делит сторону ВС в отношении СР:РВ=2:1. Прямые АР и СК пересекаются в точке М. Найдите площадь треугольника АВС, если площадь треугольника ВМС равна 4.
Дополнительные задачи
Слайд 37Прямая КР делит сторону АВ треугольника АВС в отношении АК:КВ=2:1,
а сторону ВС - в отношении ВР:РС=3:1. Медиана ВВ1 пересекает
прямую КР в точке М. При этом площадь четырехугольника В1МРС равна 17. Найдите площадь треугольника АВС.
В треугольнике АВС на основании АС взяты точки Р и Т, так что АР < АТ. Прямые ВР и ВТ делят медиану АМ на три равные части. Найдите АС, если РТ=3.
В треугольнике АВС площади 18 проведены отрезки ВМ и АК, причем точки М и К делят соответственно стороны АС и ВС в отношении АМ:МС=3:4 и ВК:КС=2:7. Найдите площадь четырехугольника СМРК, где Р – точка пересечения отрезков ВМ и АК.
На сторонах треугольника АВС взяты точки М, К и Р такие, что АМ:МВ=ВК:КС=СР:РА=2:1. Отрезки СМ и ВР пересекаются в точке А1, АК и СМ - в точке В1, АК и ВР – в точке С1. Найдите площадь треугольника АВС, если площадь треугольника А1В1С1 равна 1.
Слайд 38Теорема Менелая проста в понимании. Но трудности, связанные с освоением
этих теорем, оправданы их применением при решении задач.
Решение
задач с помощью теоремы Менелая более рационально, чем их решение другими способами, например векторным, которое требует дополнительных действий.
Я считаю, что такие теоремы должны быть включены в основной курс геометрии 7-х-9-х классов, так как решение задач с помощью этих теорем развивает мышление и логику учеников.
Теорема Менелая помогает быстро и оригинально решить задачи повышенной сложности, в том числе и задачи уровня С единого государственного экзамена.
Заключение
Слайд 391.Энциклопедия для детей. Том 11. Математика. М.: Аванта +, 2002
2.
В.В. Прасолов. Задачи по планиметрии. Часть I.
3. Володурин В.С. и
др. Пособие по элементарной геометрии. Учебное пособие для студентов физико-математических специальностей педвузов. — Оренбург, 1991.
4. Шарыгин И.Ф. Геометрия. Задачник.9—11 классы. — М.: Дрофа, 1996.
5. Б .Орач .Теорема Менелая. Квант № 3, 1991.
Список литературы