Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА
Содержание
- 1. Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА
- 2. Каждой точке прямойставиться в соответствие некоторая точка
- 3. Углы измеряются в радианной мере, а угол
- 4. Слайд 4
- 5. №1.Найти градусную меру угла, равного: а) π
- 6. №2. Найти градусную меру угла, равного :
- 7. Найти радианную меру углов, записанных в таблице
- 8. Проверим результаты вычислений
- 9. Выполнить № 223 ( 1,
- 10. Определите градусную и радианную меру Равностороннего треугольникаРавнобедренного
- 11. Закрепим полученные знанияКакой угол называется углом в
- 12. Чему равна градусная мера угла в 1
- 13. Чему равна радианная мера угла в 1º?
- 14. Найти градусную меру углов, записанных в таблицеРадианы0п/6п/4п/3п/2п
- 15. Успехов в учёбе!СПАСИБО ЗА УРОК!
- 16. Скачать презентанцию
Каждой точке прямойставиться в соответствие некоторая точка окружности. Точки (1, π/2, -1, -2) перейдут соответственнов точки окружности(М1, М2, М4, М3) Угол РО М1 –единичный иего мерой измеряютсядругие углы.
Слайды и текст этой презентации
Слайд 1 ЭЛЕМЕНТЫ ТРИГОНОМЕТРИИ
РАДИАННАЯ МЕРА УГЛА
МОУ Василёвская СОШ
Починковского р-на
Нижегородской
обл.
Слайд 2
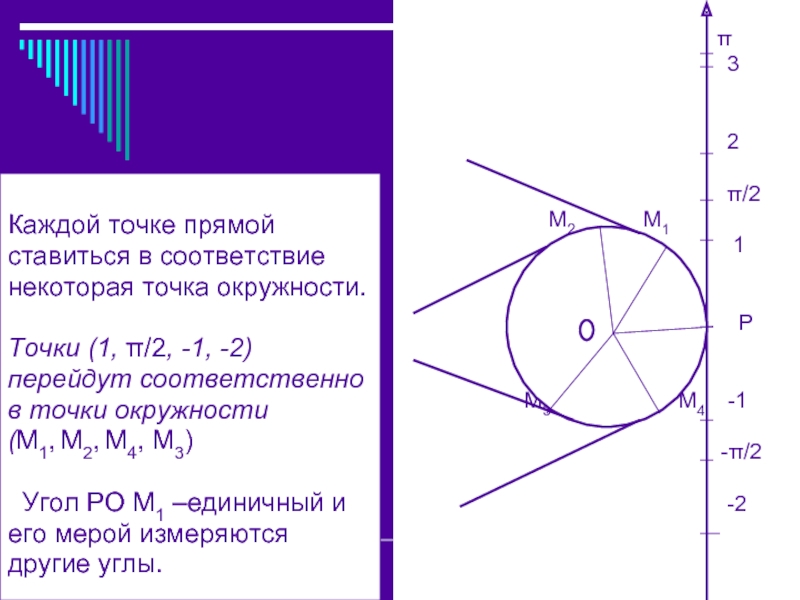
Каждой точке прямой
ставиться в соответствие
некоторая точка окружности.
Точки (1,
π/2, -1, -2)
перейдут соответственно
в точки окружности
(М1, М2, М4, М3)
Угол РО М1 –единичный иего мерой измеряются
другие углы.
π
3
2
π/2
М2 М1
1
О Р
М3 М4 -1
-π/2
-2
О
Слайд 3Углы измеряются в радианной мере, а угол РО М1 называется
углом в 1 радиан (1рад)
Центральный угол, опирающийся на
дугу, длина которой равна радиусу окружности, называется углом в 1 радиан.
М
R
Р
ОР = ОМ = R
O
Слайд 5№1.Найти градусную меру угла, равного: а) π рад; б) π/2 рад;
в) ¾ π рад
А) по формуле
находим: π рад =
180º;Б) π/2 рад = 90º;
В) ¾ π рад = 180 . 3π = 135 º.
π 4
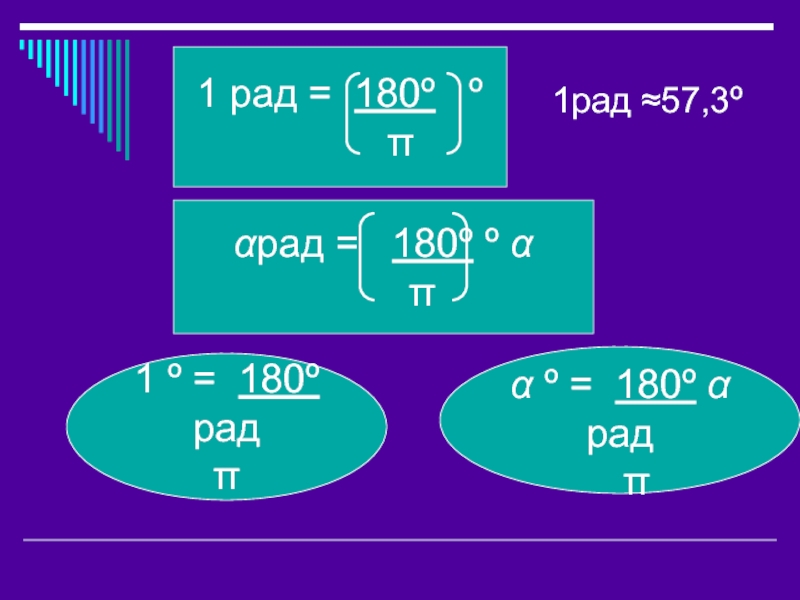
αрад = 180º º α
π
Слайд 6№2. Найти градусную меру угла, равного : а) 45 º;
б) 15 º
По формуле
находим:
А) 45 º = π/180
* 45 рад = π/4 рад;Б) 15 º = π/180 * 15 рад = π/12 рад
α º = 180º α рад
π
Слайд 10Определите градусную и радианную меру
Равностороннего треугольника
Равнобедренного
прямоугольного
треугольника
квадрата
Правильного шестиугольника
60º
π/3 рад
45º
π/4 рад
90º
π/2 рад
120º
2/3
π рад
Слайд 11Закрепим полученные знания
Какой угол называется углом в 1 радиан?
Центральный угол,
опирающийся
на дугу, длина которой равна
радиусу окружности, называется
углом
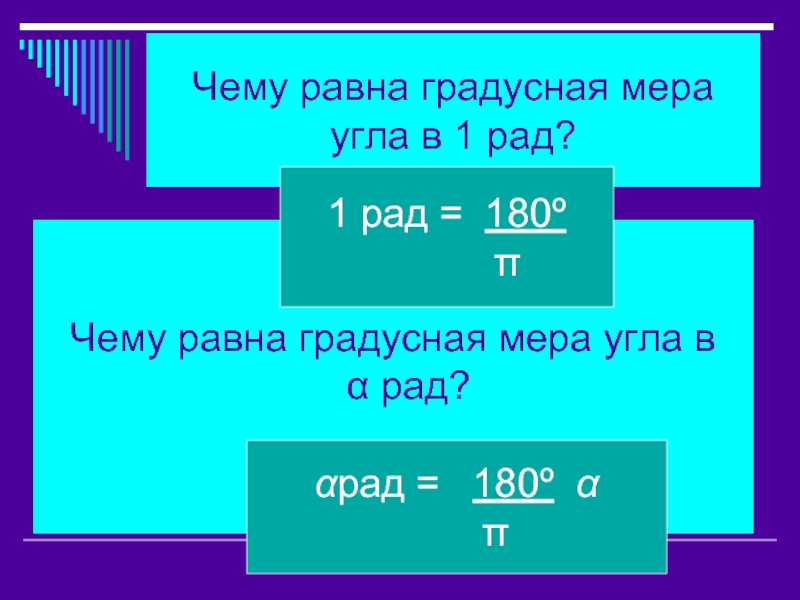
в 1 радиан.
Слайд 12Чему равна градусная мера угла в 1 рад?
Чему равна градусная
мера угла в α рад?
1 рад = 180º
π
αрад = 180º α
π
Слайд 13Чему равна радианная мера угла в 1º?
Чему равна радианная
мера угла в α º?
1 º = 180º рад
π
α º = 180º . α рад
π
Теги
