Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Евклидова и неевклидова геометрия 10 класс
Содержание
- 1. Евклидова и неевклидова геометрия 10 класс
- 2. Кто такой Евклид
- 3. Евклидовая Геометрия Евклидова
- 4. Что такое Аксиома
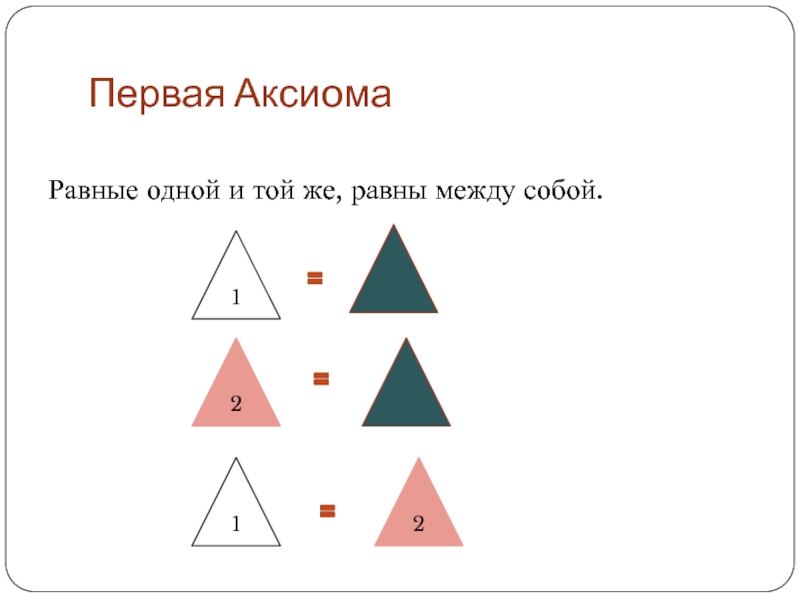
- 5. Первая АксиомаРавные одной и той же, равны между собой. 1212
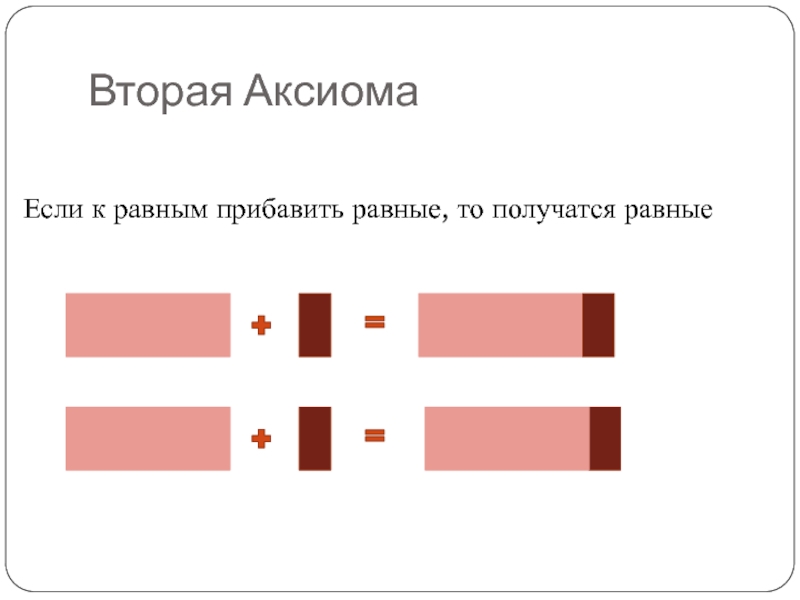
- 6. Вторая АксиомаЕсли к равным прибавить равные, то получатся равные
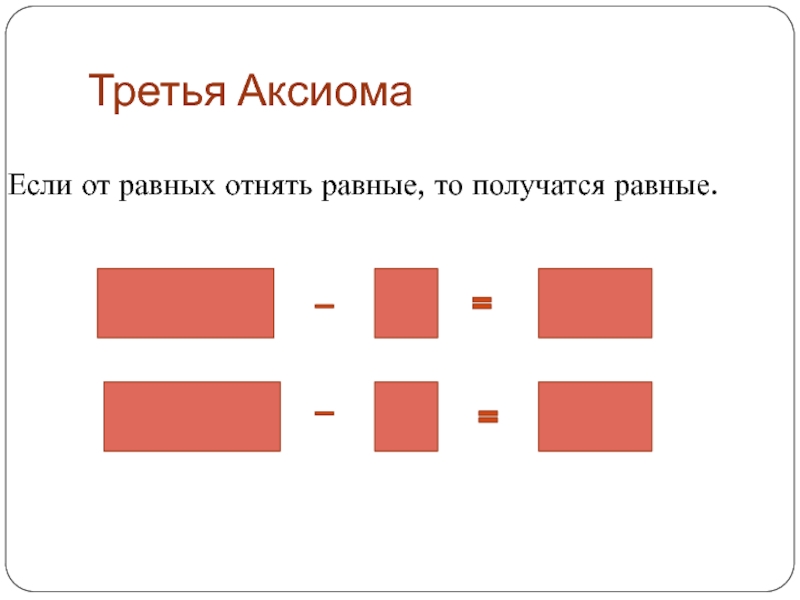
- 7. Третья АксиомаЕсли от равных отнять равные, то получатся равные.
- 8. Четвертая АксиомаСовмещаемые друг с другом равны друг другу
- 9. Что такое постулаты
- 10. О чем говорят постулатыОт всякой точки до
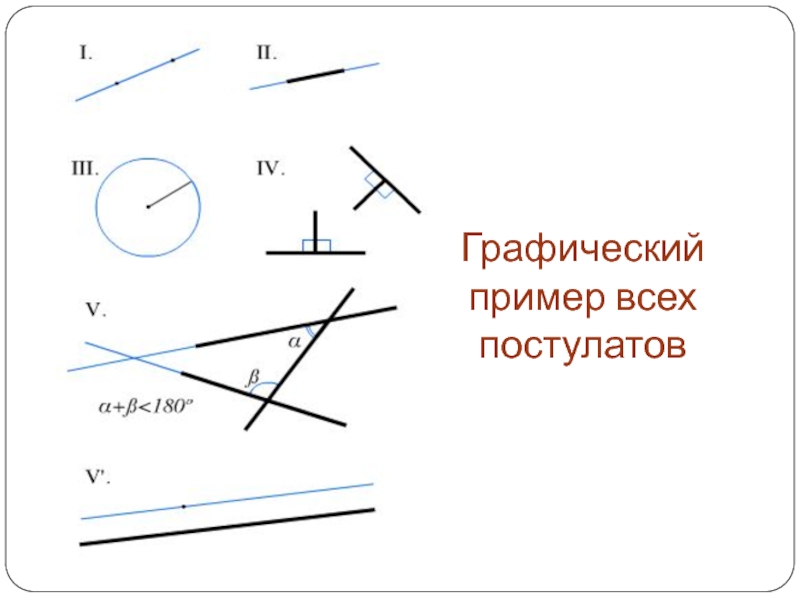
- 11. Графический пример всех постулатов
- 12. Вскоре многие
- 13. Попытки доказательства
- 14. Посидоний Учёный
- 15. Сабит ибн Курра
- 16. Омар Хайям Поэт
- 17. Таким образом, в
- 18. Николай Иванович Лобачевский (20 ноября (1 декабря) 1792г. — 12 (24)
- 19. Евклидова аксиома о параллельных гласит:
- 20. В геометрии Лобачевского, вместо неё принимается следующая
- 21. Попробуем понять смысл аксиомы Рассмотрим на плоскости
- 22. Выводы 1. Если допустить, что PT
- 23. Параллели в точке P к прямой
- 24. C помощью этих прямых все прямые, проходящие через точку P разбиваются на 2 класса:
- 25. Прямые, пересекающие
- 26. II класс: Прямые, не пресекающие AIA
- 27. Основные факты геометрии Лобачевского (отличия от геометрии
- 28. 4. Две различные прямы на плоскости могут
- 29. Расходящиеся прямые Они имеют
- 30. Трем типам пар прямых на плоскости соответствуют
- 31. Лобачевский подверг глубокой
- 32. Псевдосфера Итальянский математик Э.
- 33. Модель Клейна В 1871 году Клейн предложил
- 34. Модель Пуанкаре Позже Пуанкаре, в
- 35. Благодарю за внимание!
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Кто такой Евклид
Евклид — древнегреческий математик,
автор первого из дошедших до нас теоретических трактатов по математике.
Его главная работа «Начала». Cодержит изложение
планиметрии, стереометрии и ряда вопросов теории чисел; в ней он подвёл итог предшествующему развитию греческой математики и создал фундамент дальнейшего развития математики.
Слайд 3Евклидовая Геометрия
Евклидова геометрия — геометрическая теория, основанная
на системе аксиом
К Евклидовой геометрии относится
преобразование инверсии, вопросы сферической геометрии, элементы геометрических построений, теорию измерения геометрических величин и другие вопросы. В Евклидовой геометрии четыре аксиомы и пять постулатов. Слайд 4Что такое Аксиома
Аксиома — исходное положение
какой-либо теории, принимаемое в рамках данной теории истинным без требования
доказательства и используемое в основе доказательства других ее положений.Слайд 9Что такое постулаты
Постулат -это
утверждение которое берут в основу теории.
Постулат можно
было бы считать равноценным аксиоме, но на самом деле есть отличие: само слово означает, что это - утверждение, базовое утверждение для какой-то гипотезы.Это отличие - общепринятое обозначение тех утверждений, которые пока еще не очевидны эмпирически. Если на основе постулата строится непротиворечивая теория, описывающая свою абстракцию реальности, то есть основания попытаться найти такие условия в действительности, в которых этот постулат окажется равноценным аксиоме: т.е. можно будет доказать его объективную достоверность. Не раз случалось, что постулированное оказывалось неадекватным развиваемой теории, и от такого постулата отказывались.
Слайд 10О чем говорят постулаты
От всякой точки до всякой точки можно
провести прямую.
Ограниченную прямую можно непрерывно продолжать по прямой.
Из всякого центра
всяким раствором может быть описан круг.Все прямые углы равны между собой.
Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.
Слайд 12 Вскоре многие люди пытались доказать
пятый постулат Евклида.
Пятый постулат чрезвычайно
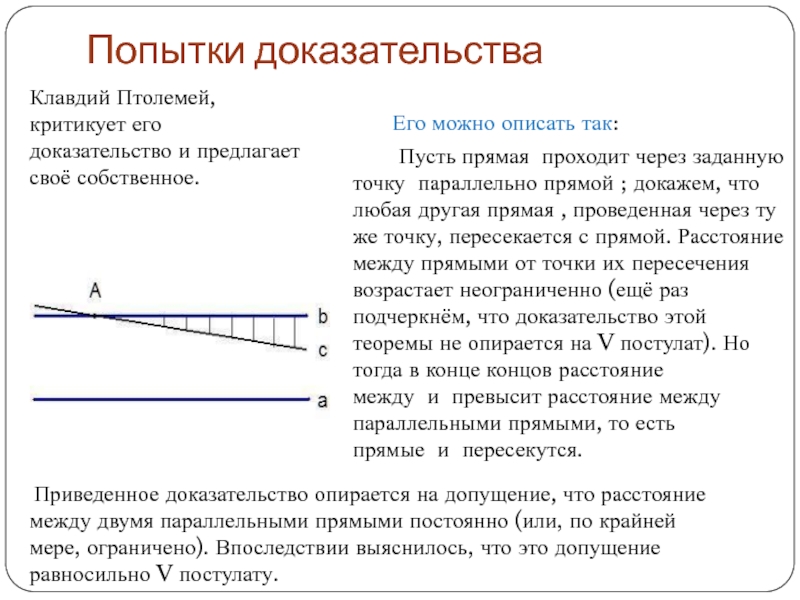
сильно отличается от других постулатов Евклида, простых и интуитивно очевидных. Поэтому в течение двух тысячелетий не прекращались попытки исключить его из списка аксиом и вывести как теорему. Все эти попытки окончились неудачей. Несмотря на отрицательный результат, эти поиски не были напрасны, так как в конечном счёте привели к полному пересмотру научных представлений о геометрии Вселенной.Слайд 13Попытки доказательства
Его можно описать так:
Пусть прямая проходит через заданную
точку параллельно прямой ; докажем, что любая другая прямая , проведенная через ту же точку, пересекается с прямой. Расстояние между прямыми от точки их пересечения возрастает неограниченно (ещё раз подчеркнём, что доказательство этой теоремы не опирается на V постулат). Но тогда в конце концов расстояние между и превысит расстояние между параллельными прямыми, то есть прямые и пересекутся.Клавдий Птолемей, критикует его доказательство и предлагает своё собственное.
Приведенное доказательство опирается на допущение, что расстояние между двумя параллельными прямыми постоянно (или, по крайней мере, ограничено). Впоследствии выяснилось, что это допущение равносильно V постулату.
Слайд 14Посидоний
Учёный I века до
н. э. Посидоний предложил определить параллельные как прямые, на всём протяжении равноудалённые
друг от друга. Из такого определения легко выводится пятый постулат. Однако определение Посидония некорректно: ниоткуда не следует, что линия, равноудалённая от данной прямой, есть прямая.Слайд 15Сабит ибн Курра
Сабит ибн Курра (IX
век) дал два доказательства;
В
первом он опирается на предположение, что если две прямые удаляются друг от друга с одной стороны, они обязательно приближаются с другой стороны. Во втором, как и Посидоний, он исходит из существования равноотстоящих прямых, причём этот факт ибн Курра пытается вывести из представления о «простом движении», т. е. о равномерном движении на фиксированном расстоянии от прямой (ему представляется очевидным, что траектория такого движения — тоже прямая).
Каждое из двух упомянутых утверждений Ибн Курры эквивалентно V постулату.
Слайд 16Омар Хайям
Поэт и математик Омар Хайям подверг
критике попытки ввести в геометрию механическое движение.
Он предложил заменить V постулат на другой, более простой: две сходящиеся прямые пересекаются, и невозможно, чтобы две сходящиеся прямые расходились в направлении схождения. Каждая из двух частей этого утверждения равносильна постулату Евклида.Слайд 17 Таким образом, в конце XIX века
проблема параллелей оставалась нерешенной.
В 1826г. Лобачевский дал окончательное, но совсем неожиданное решение проблемы.Он создал новую геометрию, заменив Евклидов постулат более общей аксиомой параллельности и сохранив прочие аксиомы и постулаты.
Слайд 18Николай Иванович Лобачевский
(20 ноября (1 декабря) 1792г.
— 12 (24) февраля 1856г.
Русский математик, создатель неевклидовой геометрии,
в течение 40 лет преподавал в Казанском
университете, в том числе 19 лет руководил им в должности ректора.Слайд 19Евклидова аксиома о параллельных гласит:
Через точку,
не лежащую на данной прямой, проходит не более одной прямой,
лежащей с данной прямой в одной плоскости и не пересекающей её.b
a
A
Слайд 20В геометрии Лобачевского, вместо неё принимается следующая аксиома:
Через точку, не лежащую на данной прямой, проходят по
крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.Слайд 21Попробуем понять смысл аксиомы
Рассмотрим на плоскости
ААI- произвольная прямая
P-точка вне
прямой
PQ-перпендикуляр к прямой ААI
M-переменная точка на луче QA
При движении точки M по лучу QA от точки Q к точке A прямая PM поворачивается против часовой стрелки. Таким образом имеется какое-то предельное положение (луч PT) к которому приближается луч PM, когда M неограниченно удаляется по лучу QA.M
M1
M2
A
P
T
АI
Q
B
α
Слайд 22Выводы
1. Если допустить, что PT совпадает с PB,
мы получим постулат параллельности Евклида.
2. Можно сделать более
общее допущение (оно и было принято Лобачевским) Аксиома Лобачевского:
Луч PT образует с PQ некоторый угол α < 900 . Этот угол Лобачевский назвал углом параллельности для отрезка PQ .
Прямая PT названа Лобачевским параллелью к
ААI в точке P в направлении ААI
Слайд 23 Параллели в точке P к прямой ААI в двух
направлениях
Рассмотрев симметрию с осью PQ
видно, что ИИI , симметричная TIT , также проходит через точку P и не имеет общих точек с QA. Эти две прямые TIT и ИИI названы параллелями в точке P к прямой ААI в двух ее направлениях соответственно ААIи АIА.Слайд 25
Прямые, пересекающие AI А
( это прямые, содержащиеся объединении двух вертикальных углов
ИIРТ и ИРТI .Множеству таких прямых принадлежит прямая PQ ).
I класс:
Слайд 26II класс:
Прямые, не пресекающие AIA
(параллели TIT и ИИI
, а также все прямые, содержащиеся в объединении вертикальных углов
ТРИ и ИIРТ; этот класс содержит и прямую ВI В).Прямые этого класса, отличные от параллелей, Лобачевский назвал разводными. Теперь их называют расходящимися или сверхпараллелями к прямой AIA.
Слайд 27Основные факты геометрии Лобачевского
(отличия от геометрии Евклида)
1. Сумма углов треугольника
меньше 1800 и может быть неодинакова у различных треугольников.
2. Нет
подобных фигур( т.к. все теоремы о подобии выводятся только с помощью Евклидовой теории параллелей).
3. Появился признак равенства треугольников по трем углам.
Слайд 284. Две различные прямы на плоскости могут образовать пару только
одного из трех типов.
Пересекающиеся прямые
Параллельные прямые
В направлении
параллельности они неограниченно сближаются, аналогично тому, как гипербола приближается к своей асимптоте. Иначе говоря, расстояние от точек одной прямой до другой прямой делается сколь угодно малым, в направлении противоположном это расстояние неограниченно возрастает. а
b
O
n
Слайд 29Расходящиеся прямые
Они имеют один общий перпендикуляр.
По обе стороны перпендикуляра прямые расходятся, и
притом неограниченно.Слайд 30Трем типам пар прямых на плоскости соответствуют три типа пучков
прямых, покрывающих всю плоскость
Пучок 1-го рода
Множество
всех прямых, проходящих через одну точку.Пучок 2-го рода
Множество всех прямых плоскости, перпендикулярных к одной прямой, которая называется базой пучка.
Пучок 3-го рода
Множество всех прямых плоскости, параллельных одной прямой в заданном направлении; любые две прямые такого пучка параллельны между собою в направлениях, соответствующих заданному.
Слайд 31 Лобачевский подверг глубокой разработке проблемы своей
геометрии; в частности, он находил с помощью методов дифференциального и
интегрального исчисления площади фигур, ограниченные криволинейными контурами и объемы тел.Лобачевский умер, а его геометрия еще не получила признания, оно пришло лишь через 12-15 лет после его смерти.
Основную роль в признании идей Лобачевского сыграли исследования итальянского ученого Е. Бельтрами, немца Ф. Клейна, француза А. Пуанкаре.
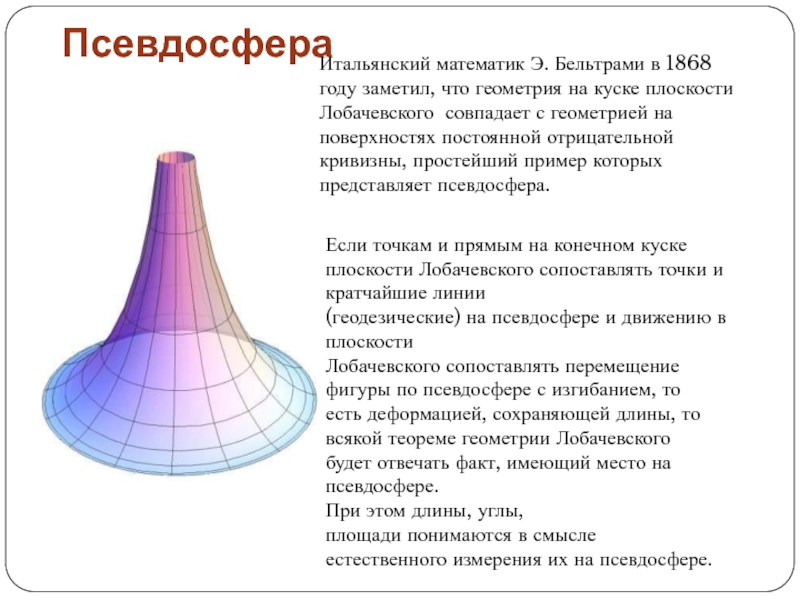
Слайд 32Псевдосфера
Итальянский математик Э. Бельтрами в 1868 году заметил, что геометрия
на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной
отрицательной кривизны, простейший пример которыхпредставляет псевдосфера.
Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии
(геодезические) на псевдосфере и движению в плоскости
Лобачевского сопоставлять перемещение
фигуры по псевдосфере с изгибанием, то
есть деформацией, сохраняющей длины, то
всякой теореме геометрии Лобачевского
будет отвечать факт, имеющий место на
псевдосфере.
При этом длины, углы,
площади понимаются в смысле
естественного измерения их на псевдосфере.
Слайд 33Модель Клейна
В 1871 году Клейн предложил первую полноценную
модель плоскости
Лобачевского.
Плоскостью служит внутренность круга,
прямой — хорда круга
без концов, а точкой — точка внутри круга. «Движением» назовём
любое преобразование круга в самого себя,
которое переводит хорды в хорды.
Соответственно, равными называются фигуры
внутри круга, переводящиеся одна в другую
такими преобразованиями. Тогда оказывается,
что любой геометрический факт, описанный на
таком языке, представляет теорему или
аксиому геометрии Лобачевского.
Иными словами, всякое утверждение геометрии
Лобачевского на плоскости есть не что иное,
как утверждение евклидовой геометрии,
относящееся к фигурам внутри круга, лишь
пересказанное в указанных терминах.
Евклидова аксиома о параллельных здесь явно не
выполняется, так как через точку , не лежащую на
данной хорде а (то есть «прямой»), проходит сколько
угодно не пересекающих её хорд («прямых»)
Слайд 34Модель Пуанкаре
Позже Пуанкаре, в связи с
задачами теории функций
комплексного переменного дал
другую модель.
За плоскость Лобачевского
принимается внутренность круга, прямыми
считаются дуги окружностей,
перпендикулярных окружности
данного круга, и его диаметры,
движениями — преобразования,
получаемые комбинациями
инверсий относительно
окружностей, дуги которых служат
прямыми.
Модель Пуанкаре замечательна тем,
что в ней углы изображаются
обычными углами.