Слайд 4
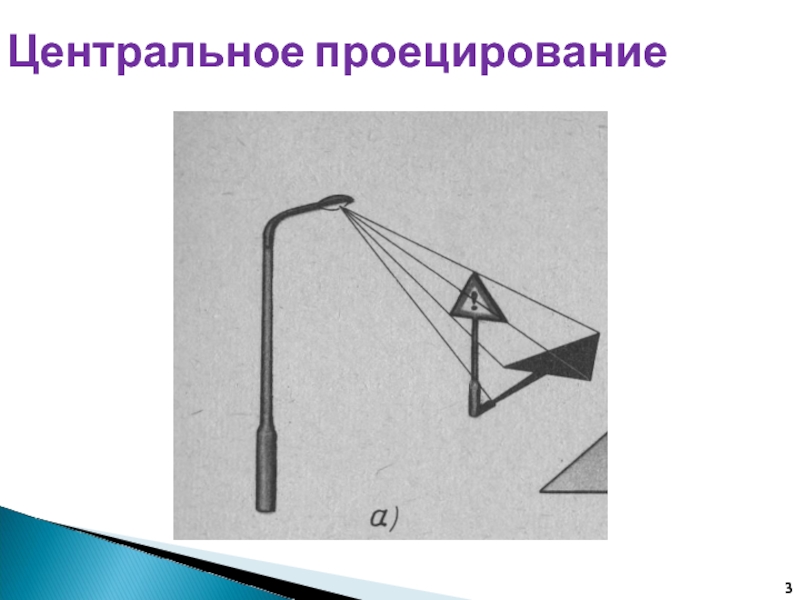
Центральное проецирование
О
A
B
C
a
c
b
Слайд 6Параллельное проецирование
A
B
C
D
a
b
c
d
Слайд 8
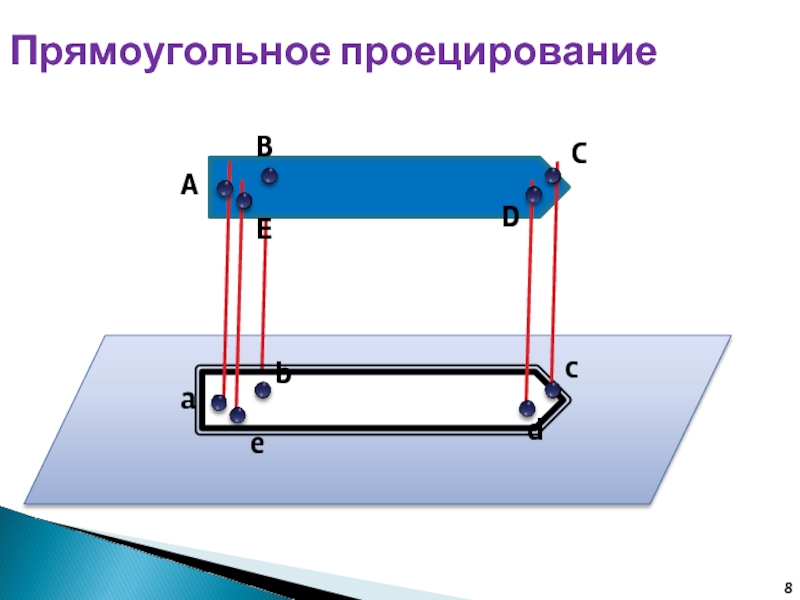
Прямоугольное проецирование
A
B
C
D
E
a
b
c
d
e
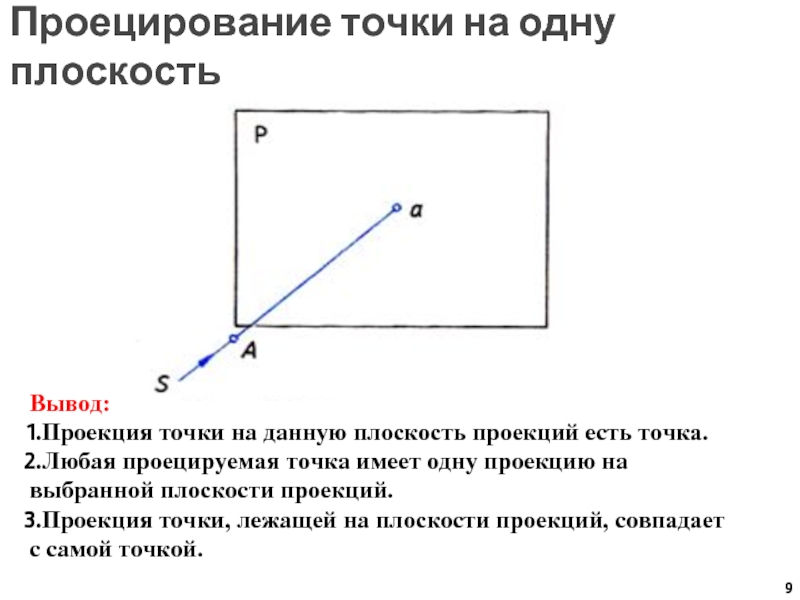
Слайд 9Проецирование точки на одну плоскость
Вывод:
Проекция точки на данную плоскость проекций
есть точка.
Любая проецируемая точка имеет одну проекцию на выбранной плоскости
проекций.
Проекция точки, лежащей на плоскости проекций, совпадает
с самой точкой.
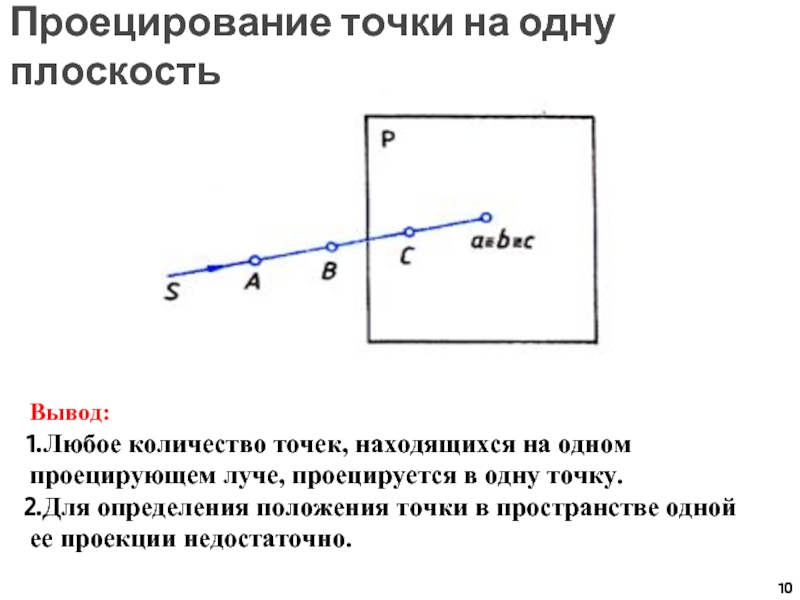
Слайд 10Проецирование точки на одну плоскость
Вывод:
Любое количество точек, находящихся на одном
проецирующем луче, проецируется в одну точку.
Для определения положения точки в
пространстве одной ее проекции недостаточно.
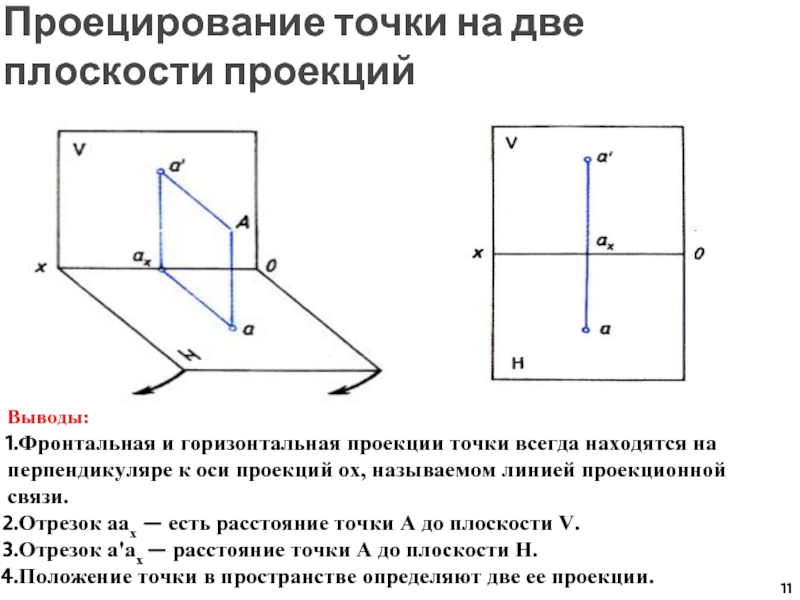
Слайд 11Проецирование точки на две плоскости проекций
Выводы:
Фронтальная и горизонтальная проекции точки
всегда находятся на перпендикуляре к оси проекций ох, называемом линией
проекционной связи.
Отрезок аах — есть расстояние точки А до плоскости V.
Отрезок а'ах — расстояние точки А до плоскости Н.
Положение точки в пространстве определяют две ее проекции.
Слайд 12Прямоугольное проецирование точки на три плоскости проекций.
Слайд 13Построение третьей проекции точки по двум заданным.
Слайд 14Построение третьей проекции точки по двум заданным.
Слайд 15По двум проекциям точки А а' и а" найдите третью
ее проекцию
Задание
а
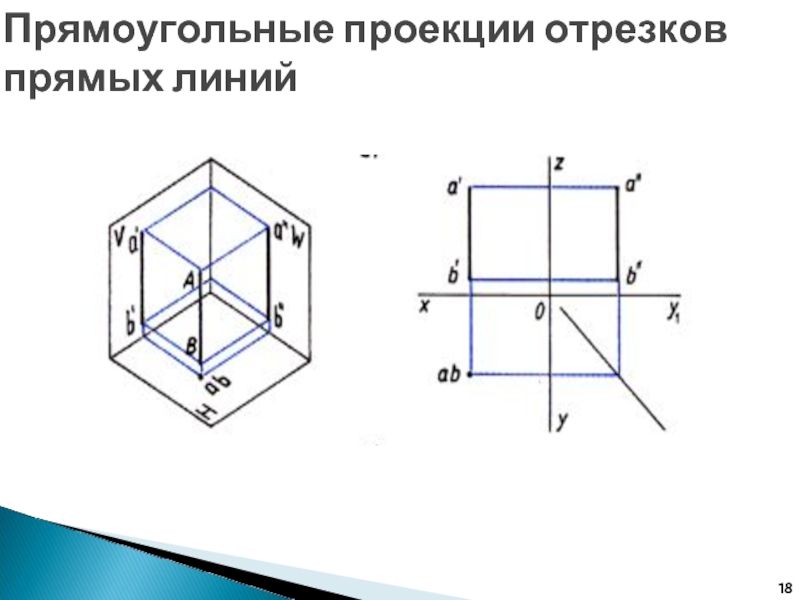
Слайд 16Прямоугольные проекции отрезков прямых линий
Слайд 17Прямоугольные проекции отрезков прямых линий
Слайд 18Прямоугольные проекции отрезков прямых линий
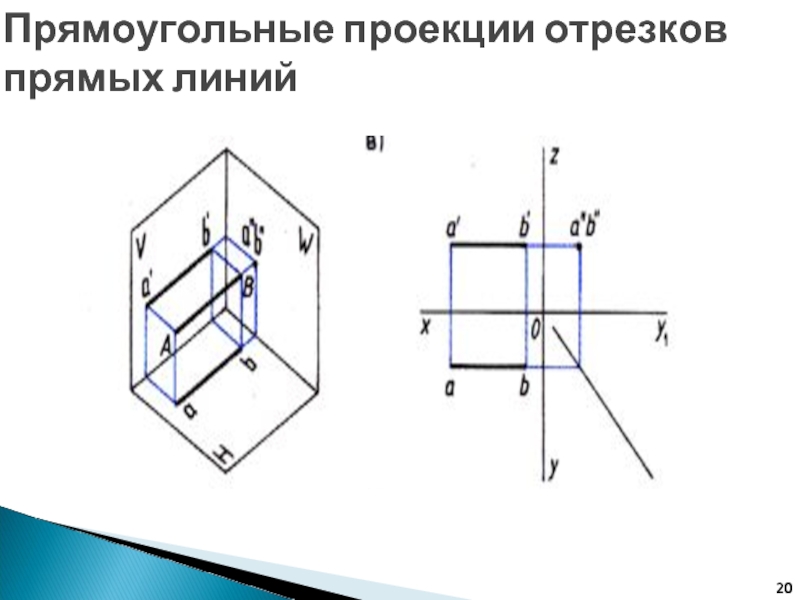
Слайд 19Прямоугольные проекции отрезков прямых линий
Слайд 20Прямоугольные проекции отрезков прямых линий
Слайд 21Прямоугольные проекции отрезков прямых линий
Вывод:
Проекция отрезка прямой, полученная при прямоугольном
проецировании на плоскость проекций, не может быть больше самого отрезка.
Если
отрезок прямой параллелен плоскости проекций, то на нее он спроецируется в натуральную величину.
Если отрезок прямой перпендикулярен плоскости проекций, то на нее он спроецируется в точку.
Если в пространстве отрезок прямой наклонен к плоскости проекций, он проецируется на нее с искажением (т. е. размер проекции отрезка будет меньше действительного).
Слайд 22По координатам отрезка постройте его проекции на три плоскости
I вариант:
А(5,0,4); В(0,4,0)
II вариант: C(0,0,5); D(3,4,6)
III вариант: E(0,4,0); F(4,7,5)
Ivвариант: G(3,4,6); H(2,1,3)
Домашнее
задание