Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
КОНУС
Содержание
- 1. КОНУС
- 2. Нас окружает множество предметов
- 3. КОНУС
- 4. Задача Какова площадь поверхности воронки,
- 5. Задача Сколько квадратных метров брезента потребуется для сооружения палатки конической формы?
- 6. КОНУСПусть дана некоторая плоскость α.
- 7. КОНУСПроведём в плоскости α замкнутую кривую линию L.L
- 8. КОНУССоединим точку А, не лежащую в плоскости α, с замкнутой кривой линией L. LА
- 9. КОНУСОтрезки, соединяющие точку А с замкнутой кривой линией L, образуют коническую поверхность.LА
- 10. КОНУСТело, ограниченное конической поверхностью и плоскостью, пересекающей её по замкнутой кривой, называется конусом.LА
- 11. Назовите предметы, которые имеют коническую поверхность
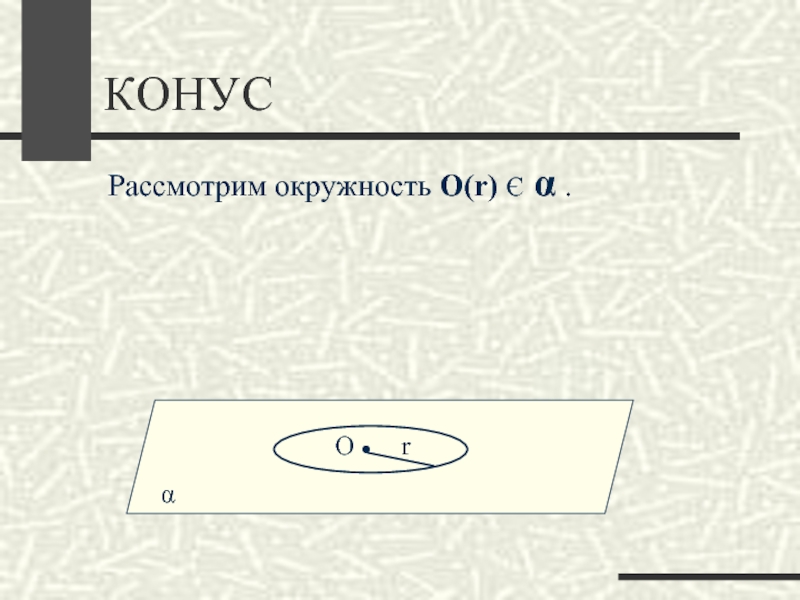
- 12. КОНУСαРассмотрим окружность О(r) Є α .
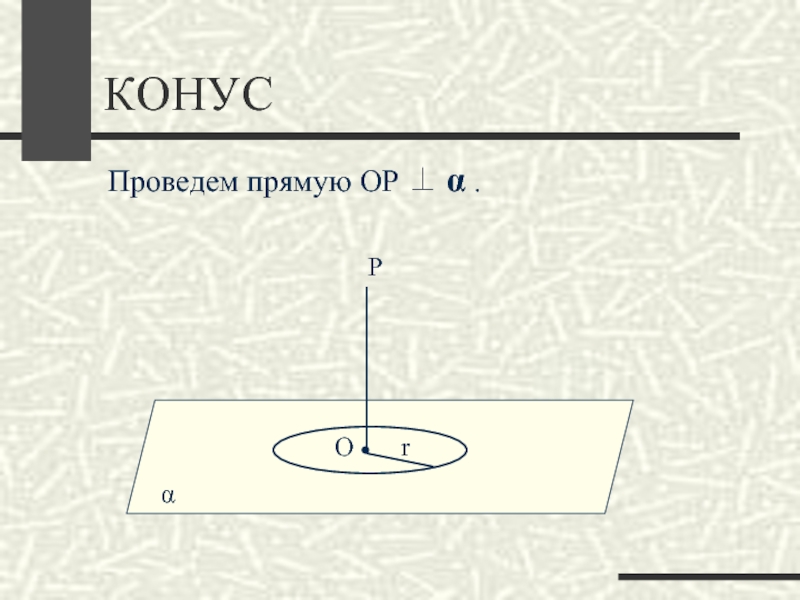
- 13. КОНУСαПроведем прямую ОР ⊥ α .ОrР
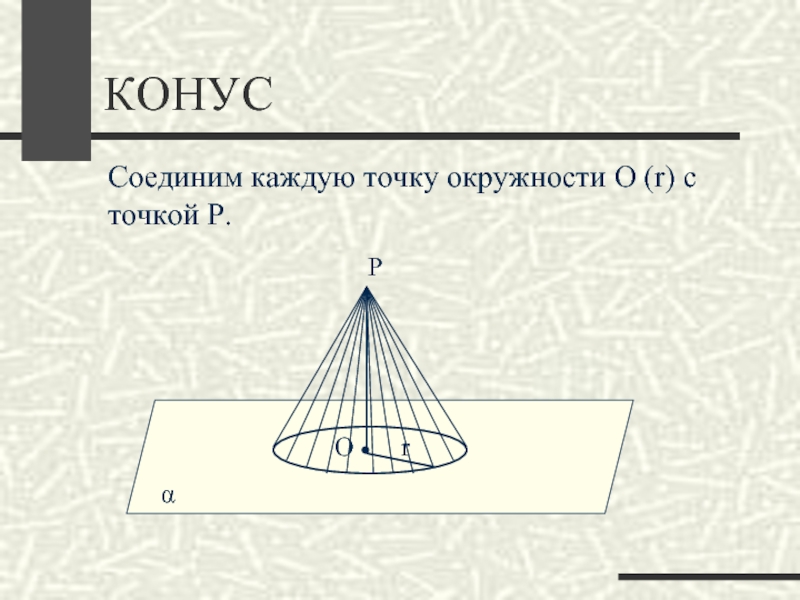
- 14. КОНУСαСоединим каждую точку окружности О (r) с точкой Р.ОrР
- 15. КОНУСПоверхность, образованная отрезками, соединяющими каждую точку окружности
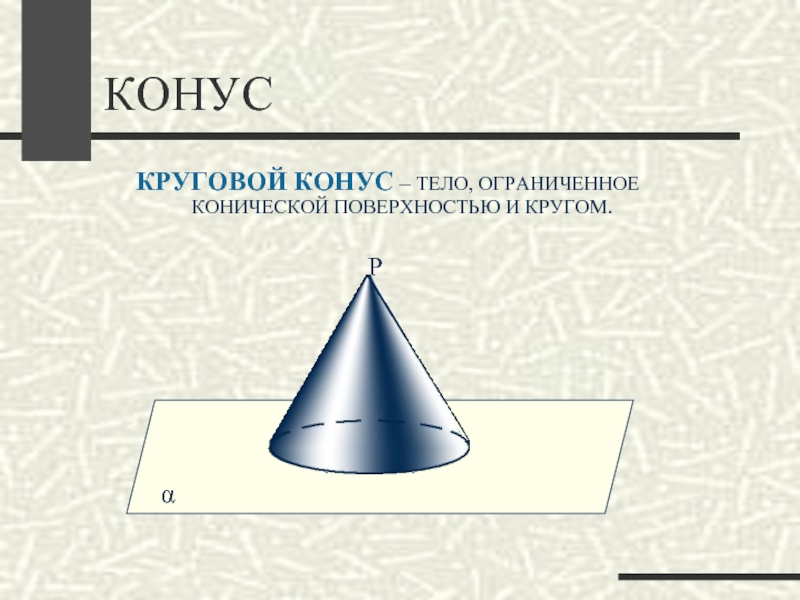
- 16. КОНУСКРУГОВОЙ КОНУС – ТЕЛО, ОГРАНИЧЕННОЕ КОНИЧЕСКОЙ ПОВЕРХНОСТЬЮ И КРУГОМ.αОrР
- 17. КОНУСЭЛЕМЕНТЫ КОНУСАКоническая поверхность – боковая поверхность конуса
- 18. КОНУСЭЛЕМЕНТЫ КОНУСАКруг – основание конуса
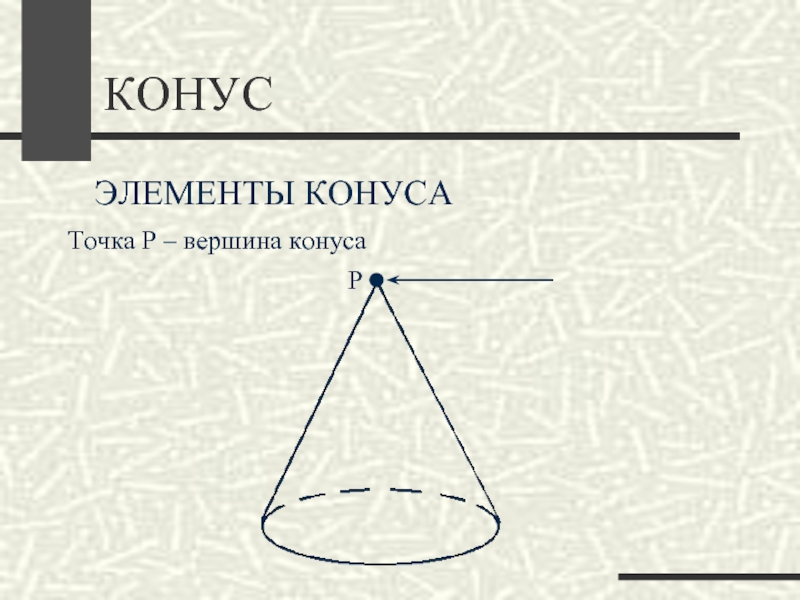
- 19. КОНУСЭЛЕМЕНТЫ КОНУСАТочка Р – вершина конуса
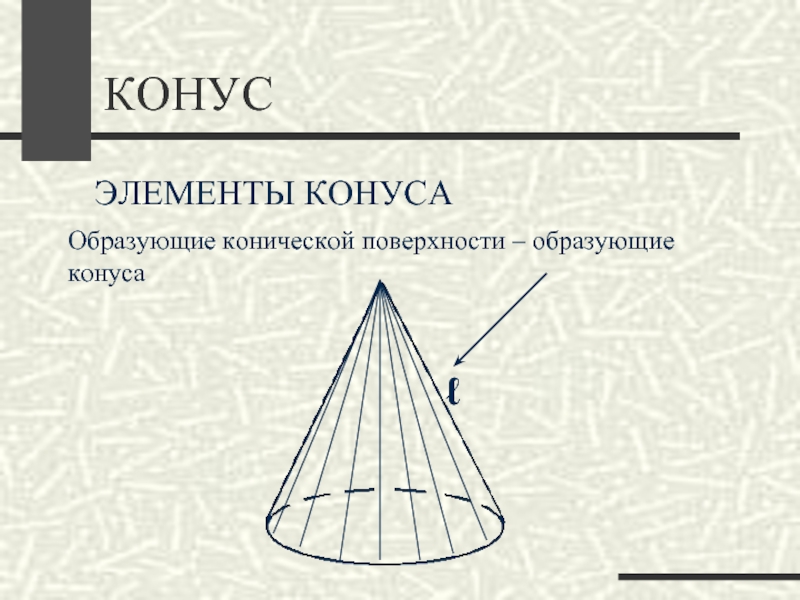
- 20. КОНУСЭЛЕМЕНТЫ КОНУСАОбразующие конической поверхности – образующие конусаℓ
- 21. КОНУСЭЛЕМЕНТЫ КОНУСА Прямая, проходящая через центр основания и вершину – ось конуса
- 22. КОНУСЭЛЕМЕНТЫ КОНУСАПерпендикуляр, опущенный из вершины на плоскость
- 23. КОНУСЭЛЕМЕНТЫ КОНУСАРадиус основания конуса – радиус конусаr
- 24. КОНУСЭЛЕМЕНТЫ КОНУСА:Боковая поверхность(коническая поверхность)ОбразующиеОснование (круг)ВершинаОсьВысотаРадиус
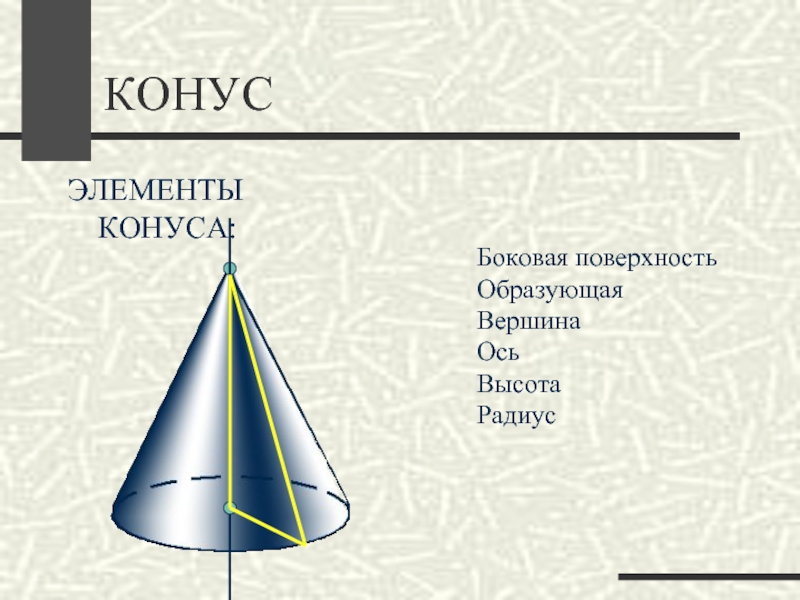
- 25. КОНУСЭЛЕМЕНТЫ КОНУСА:Боковая поверхностьВершинаОсьВысотаРадиусОбразующая
- 26. КОНУСКОНУС – ТЕЛО ВРАЩЕНИЯКонус может быть получен
- 27. КОНУССЕЧЕНИЯ КОНУСАСечения, проходящее через ось(осевые)Сечения, перпендикулярные оси
- 28. Конические сечения конуса – линии пересечения секущих
- 29. КОНУСКасательная плоскость – плоскость, проходящая через образующюю и перпендикулярная плоскости осевого сечения
- 30. Если плоскостью, параллельной основанию конуса, отсечь от
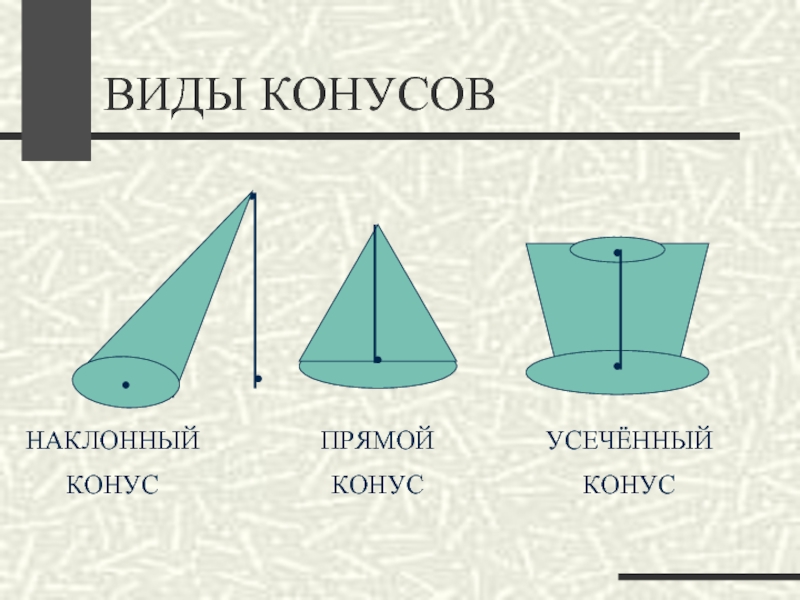
- 31. ВИДЫ КОНУСОВНАКЛОННЫЙКОНУСПРЯМОЙКОНУСУСЕЧЁННЫЙКОНУС
- 32. КОНУС
- 33. Так выглядит развертка конуса Развёрткой конуса
- 34. Задача №1 Какова площадь поверхности
- 35. Для решения задачи надо измерить:
- 36. Задача №2 Сколько квадратных метров
- 37. Задача Решение: Sбок.= πRℓR=D:2 =
- 38. Задача №3
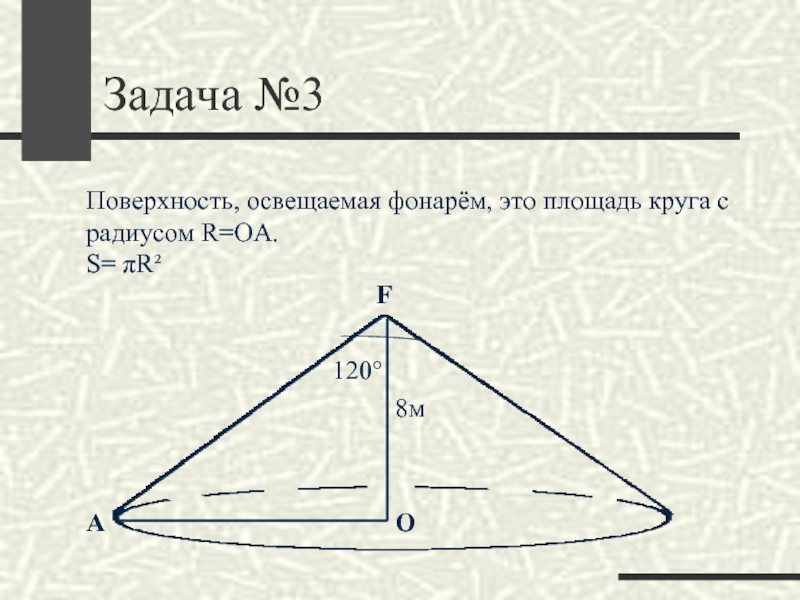
- 39. Задача №3FОПоверхность, освещаемая фонарём, это площадь круга с радиусом R=ОА.S= πR²120°8мА
- 40. Задача №3 (решение)Решение:_ FАО= 180°-120°/2=30° FA=8•2=16
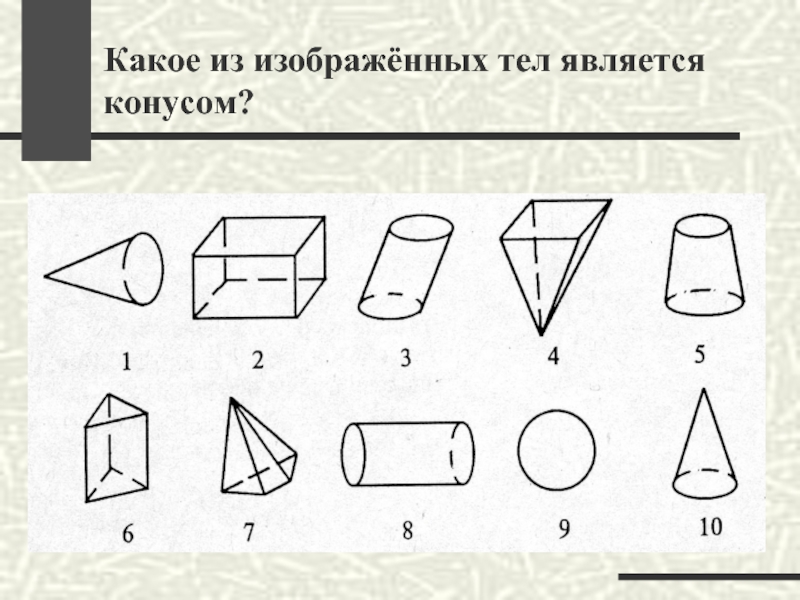
- 41. Какое из изображённых тел является конусом?
- 42. Ответьте на вопрос и запишите ответы в
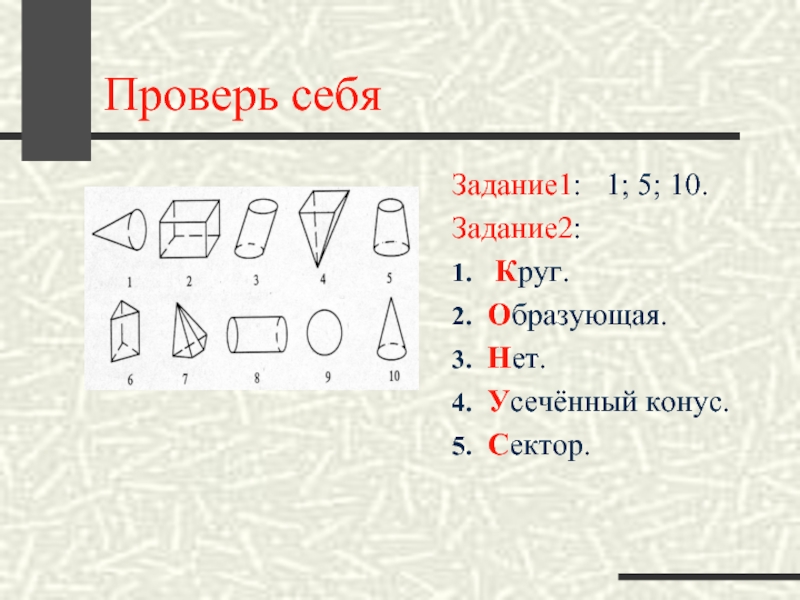
- 43. Проверь себяЗадание1: 1; 5; 10.Задание2:1. Круг.2. Образующая.3. Нет.4. Усечённый конус.5. Сектор.
- 44. КОНУСВопрос к размышлению? Почему пожарные вёдра имеют форму конуса?
- 45. КОНУС
- 46. Скачать презентанцию
Слайды и текст этой презентации
Слайд 5
Задача
Сколько квадратных метров брезента потребуется для сооружения
палатки конической формы?
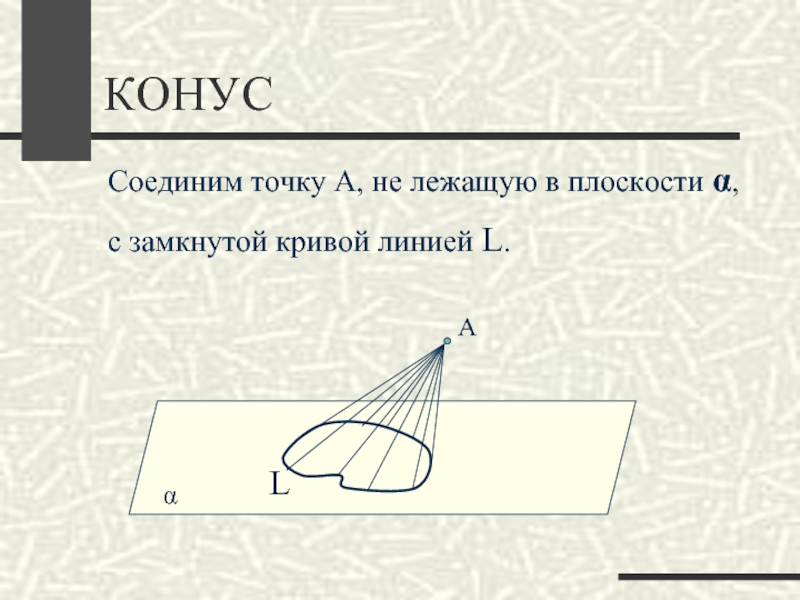
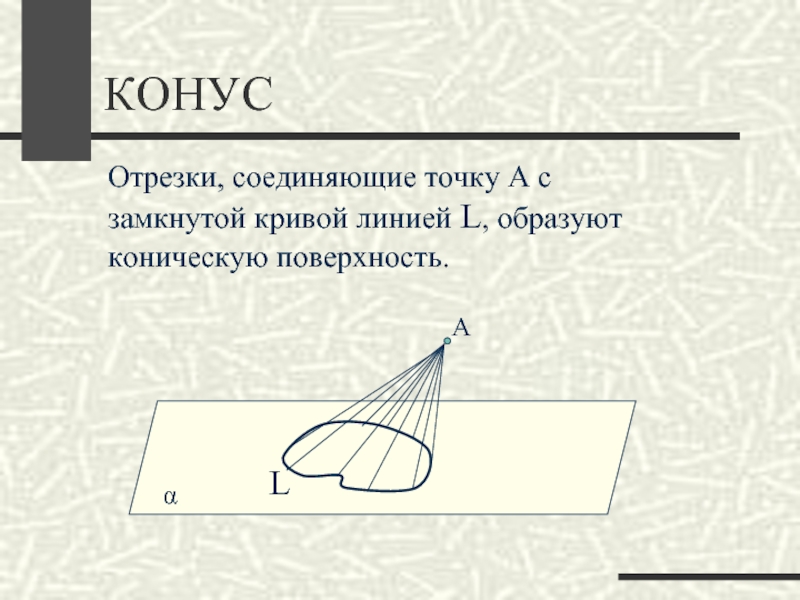
Слайд 9КОНУС
Отрезки, соединяющие точку А с замкнутой кривой линией L, образуют
коническую поверхность.
L
А
Слайд 10КОНУС
Тело, ограниченное конической поверхностью и плоскостью, пересекающей её по замкнутой
кривой, называется конусом.
L
А
Слайд 15КОНУС
Поверхность, образованная отрезками, соединяющими каждую точку окружности с точкой, лежащей
на прямой перпендикулярной плоскости этой окружности и проходящей через центр
этой окружности – это поверхность прямого кругового конуса.α
О
r
Р
Слайд 22КОНУС
ЭЛЕМЕНТЫ КОНУСА
Перпендикуляр, опущенный из вершины на плоскость основания – высота
конуса
Н
У прямого конуса ось и высота совпадают.
У наклонного конуса ось
и высота не совпадаютСлайд 24КОНУС
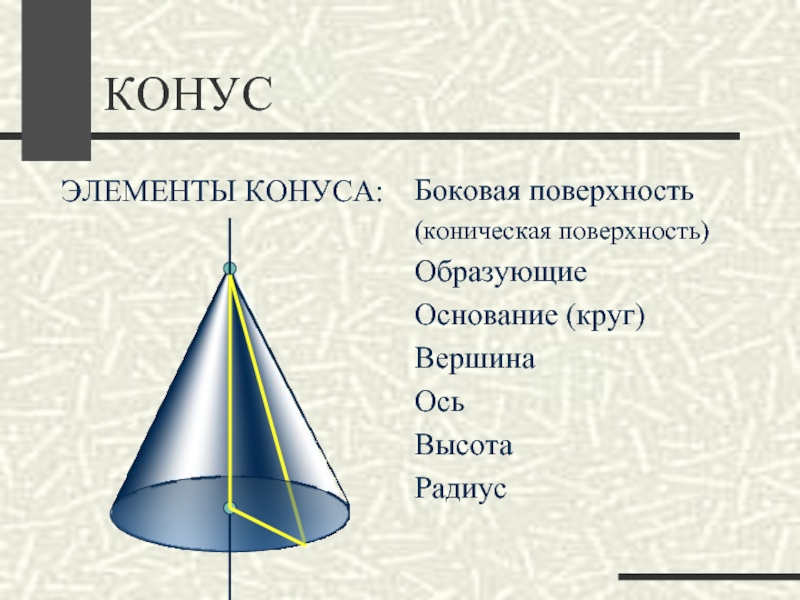
ЭЛЕМЕНТЫ КОНУСА:
Боковая поверхность
(коническая поверхность)
Образующие
Основание (круг)
Вершина
Ось
Высота
Радиус
Слайд 26КОНУС
КОНУС – ТЕЛО ВРАЩЕНИЯ
Конус может быть получен вращением прямоугольного треугольника
вокруг одного из катетов, причем этот катет будет является высотой
конуса, второй катет – радиусом конуса, а гипотенуза образующей конуса.Н
r
ℓ
Слайд 27КОНУС
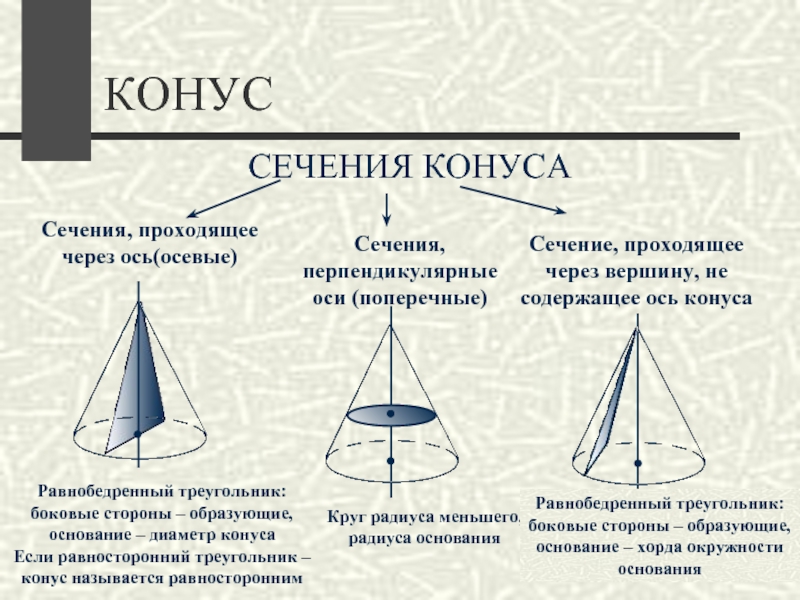
СЕЧЕНИЯ КОНУСА
Сечения, проходящее
через ось(осевые)
Сечения, перпендикулярные оси (поперечные)
Сечение, проходящее через
вершину, не содержащее ось конуса
Равнобедренный треугольник: боковые стороны – образующие,
основание – диаметр конуса Если равносторонний треугольник – конус называется равносторонним
Круг радиуса меньшего, радиуса основания
Равнобедренный треугольник: боковые стороны – образующие, основание – хорда окружности основания
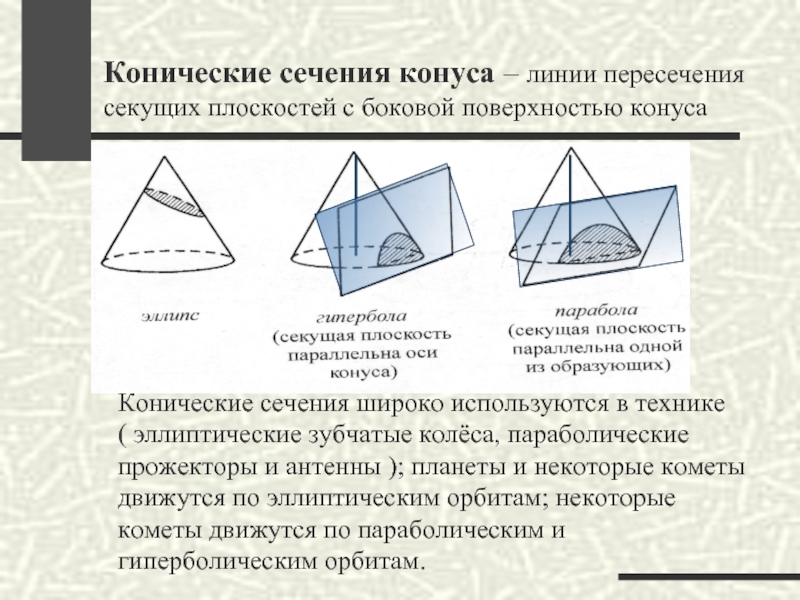
Слайд 28Конические сечения конуса – линии пересечения секущих плоскостей с боковой
поверхностью конуса
Конические сечения широко используются в технике
( эллиптические зубчатые колёса,
параболические прожекторы и антенны ); планеты и некоторые кометы движутся по эллиптическим орбитам; некоторые кометы движутся по параболическим и гиперболическим орбитам.
Слайд 29КОНУС
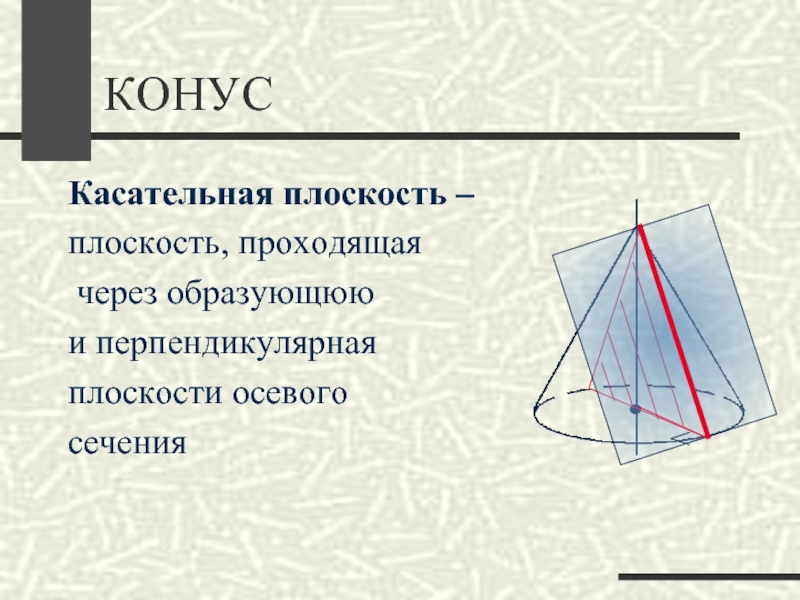
Касательная плоскость –
плоскость, проходящая
через образующюю
и перпендикулярная
плоскости
осевого
сечения
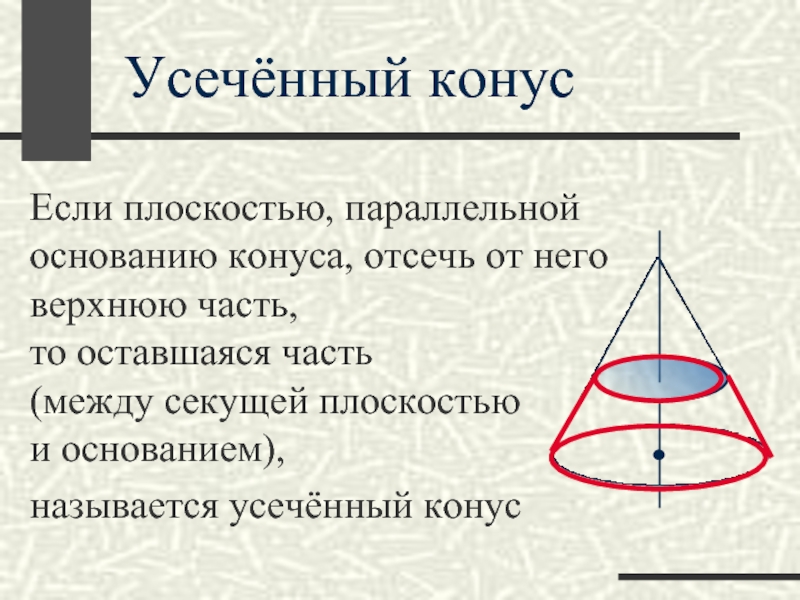
Слайд 30Если плоскостью, параллельной основанию конуса, отсечь от него верхнюю часть,
то оставшаяся часть (между секущей плоскостью и основанием), называется усечённый
конусУсечённый конус
Слайд 33Так выглядит развертка конуса
Развёрткой конуса является круговой сектор,
у которого радиус равен образующей конуса R=ℓ,
а
длина дуги равна длине окружности основания конуса L=C=2πRℓ
α
С = 2πR
Формулы
для вычисления боковой поверхности
и полной поверхности конуса:
Sбок.= πRℓ
Sосн.= πR²
Sп.п.к. =Sбок.+Sосн.= πR(R+ℓ)
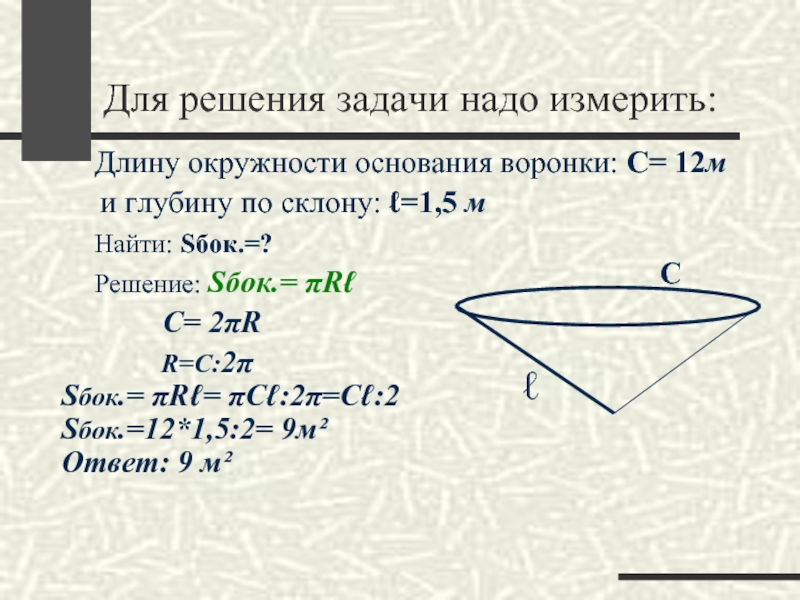
Слайд 35Для решения задачи надо измерить:
Длину окружности основания
воронки: С= 12м
и глубину по склону: ℓ=1,5
мНайти: Sбок.=?
Решение: Sбок.= πRℓ
С= 2πR
R=С:2π
Sбок.= πRℓ= πСℓ:2π=Сℓ:2
Sбок.=12*1,5:2= 9м²
Ответ: 9 м²
ℓ
С
Слайд 36
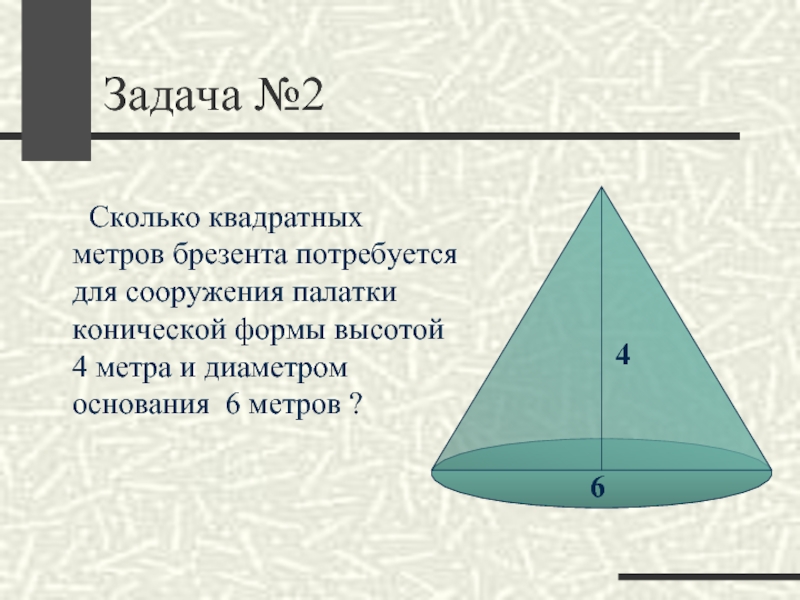
Задача №2
Сколько квадратных метров брезента потребуется для
сооружения палатки конической формы высотой 4 метра и диаметром основания
6 метров ?4
6
Слайд 37
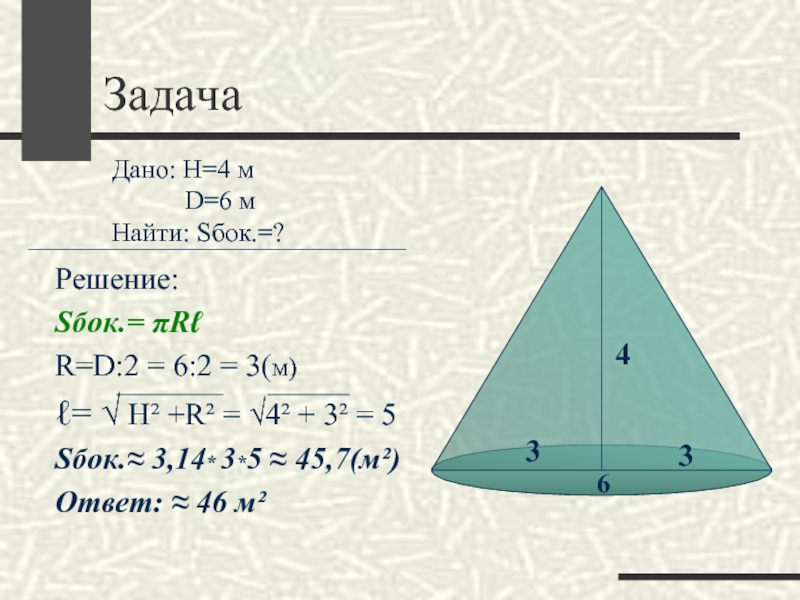
Задача
Решение:
Sбок.= πRℓ
R=D:2 = 6:2 = 3(м)
ℓ=
√ Н² +R² = √4² + 3² = 5
Sбок.≈ 3,14*
3*5 ≈ 45,7(м²)Ответ: ≈ 46 м²
4
3
3
Дано: Н=4 м
D=6 м
Найти: Sбок.=?
6
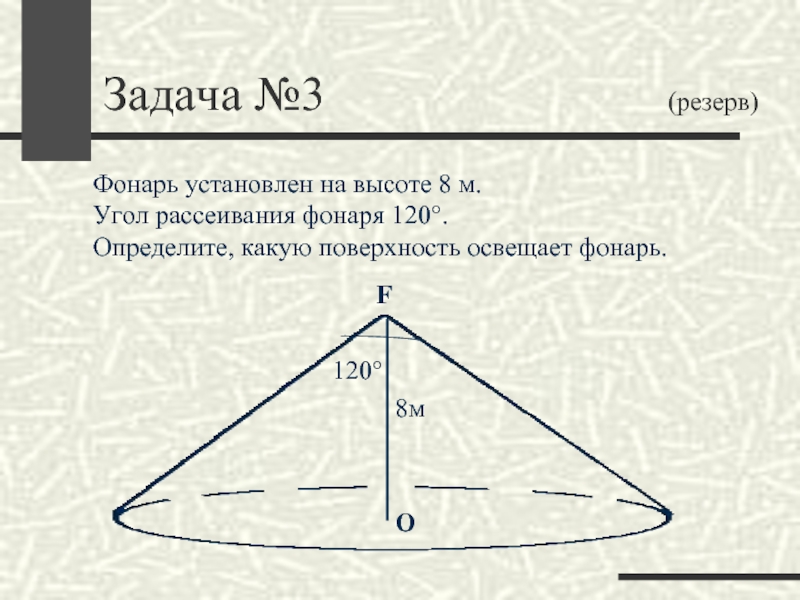
Слайд 38Задача №3
(резерв)
F
О
Фонарь установлен на высоте 8
м. Угол рассеивания фонаря 120°.
Определите, какую поверхность освещает фонарь.
120°
8м
Слайд 40Задача №3 (решение)
Решение:
_ FАО= 180°-120°/2=30°
FA=8•2=16 (катет, лежащий против
угла в 30°)
АО= √ FA²-FO² = √16²-8² = 8√3
(по теореме Пифагора)S = π (8√3)² =132π ≈ 414,5 м²
Ответ: 414,5 м²
Слайд 42Ответьте на вопрос и запишите ответы в столбик. Из первых
букв составьте слово.
Как называется:
1. Фигура, полученная при
поперечном сечении конуса?2. Отрезок, соединяющий вершину с окружностью основания?
3. Имеет ли конус центр симметрии?
4. Тело, полученное при пересечении конуса плоскостью, параллельной основанию?
5. Фигура, являющаяся боковой поверхностью конуса?