Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Смежные и вертикальные углы
Содержание
- 1. Смежные и вертикальные углы
- 2. Цели урока: 1)ознакомить учащихся с понятиями
- 3. Ход урока. 1)Организационный момент. 2)Проверка
- 4. 3) Самостоятельная тестовая работа с последующей самопроверкой.
- 5. 4) Изучение нового материала. 1.Определение:Два угла, у
- 6. Свойство вертикальных углов: вертикальные углы равны. Доказательство
- 7. 5) Закрепление изученного материалаУстно решить задачи №41,43,44
- 8. Скачать презентанцию
Цели урока: 1)ознакомить учащихся с понятиями смежных и вертикальных углов, рассмотреть их свойства; 2) научить строить угол, смежный с данным углом, изображать вертикальные углы, находить на рисунке смежные и вертикальные
Слайды и текст этой презентации
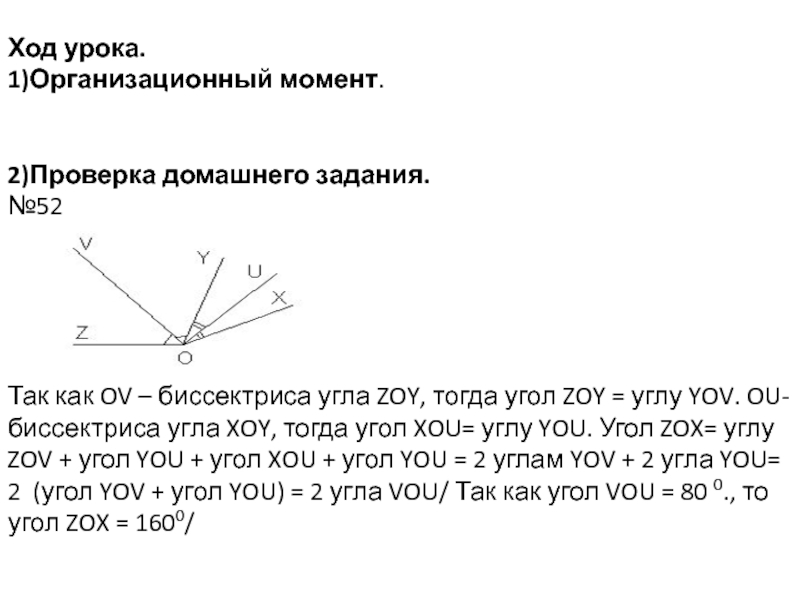
Слайд 3Ход урока. 1)Организационный момент. 2)Проверка домашнего задания. №52 Так как OV – биссектриса угла
ZOY, тогда угол ZOY = углу YOV. OU- биссектриса угла
XOY, тогда угол XOU= углу YOU. Угол ZOX= углу ZOV + угол YOU + угол XOU + угол YOU = 2 углам YOV + 2 угла YOU= 2 (угол YOV + угол YOU) = 2 угла VOU/ Так как угол VOU = 80 0., то угол ZOX = 1600/Слайд 43) Самостоятельная тестовая работа с последующей самопроверкой.
Вариант 1.
1.Дано: угол
AOB = 530, угол BOC = 910.
Найти угол COD.
А) 360
Б) 1420 В) 4602. Между сторонами угла BOC, равного 1600, проходит луч ОК. Найдите угол BOK, если разность углов BOK и KOC равно 480.
А) 1120 Б) 560 В) 1040
3) Какой из лучей а, b или с проходит между двумя другими, если угол ab =1220, угол ас = 340
угол cb = 780?
А) а Б) b В) с
Вариант 2
1.Дано: угол AOB = 340, угол DOC = 270.
Найти угол BOC.
А) 1290 Б) 1190 В) 1730
2. Между сторонами угла BOC, равного 1600, проходит луч ОК. Найдите угол KOC, если угол BOK меньше угла KOC на 120.
А) 860 Б) 740 В) 1480
3) Какой из лучей а, b или с проходит между двумя другими, если угол ab =650, угол ас = 910
угол cb = 260?
А) а Б) b В) с
Слайд 54) Изучение нового материала.
1.Определение:
Два угла, у которых одна сторона общая,
а две другие являются продолжениями одна другой, называются смежными.
Угол
AOC и угол COB – смежные. Лучи ОВ и ОA образуют одну прямую.2. Вывести свойство смежных углов в ходе выполнения следующих упражнений:
- Сколько углов изображено на рисунке? Какие это углы? (3 угла, угол АОС и угол СОВ - смежные, а угол АОВ — развернутый.)
- Существует ли какая-нибудь взаимосвязь между этими углами?
(Да, угол АОС + угол СОВ = угол АОВ.)
- Как по-другому можно записать данное равенство? Почему? (угол АОС + угол СОВ = 180°, так как угол АОВ — развернутый и его градусная мера равна 180'.)
- Для всякой ли пары смежных углов выполняется это равенство? (Да.)
- Данные равенства — математическая запись свойства смежных углов. Сформулируйте само свойство смежных углов. (Сумма смежных углов равна 180".)
3. Ввести понятие вертикальных углов в ходе выполнения следующих упражнений:
- Начертите неразвернутый угол МОК.
- Проведите лучи ОС и OD, являющиеся продолжениями сторон угла МОК.
- Сколько неразвернутых углов получилось? (Четыре – угол МОК, угол МОС, угол COD, угол KOD.)
- Назовите углы, которые не являются смежными. (угол МОК и угол COD, угол MOD и уголКОС.)
Запищите в тетради: угол МОК и угол COD — вертикальные; угол MOD и угол КОС — вертикальные.
- Попробуйте сформулировать свойство вертикальных углов и доказать его, т.е. найдите взаимосвязь между вертикальными углами.
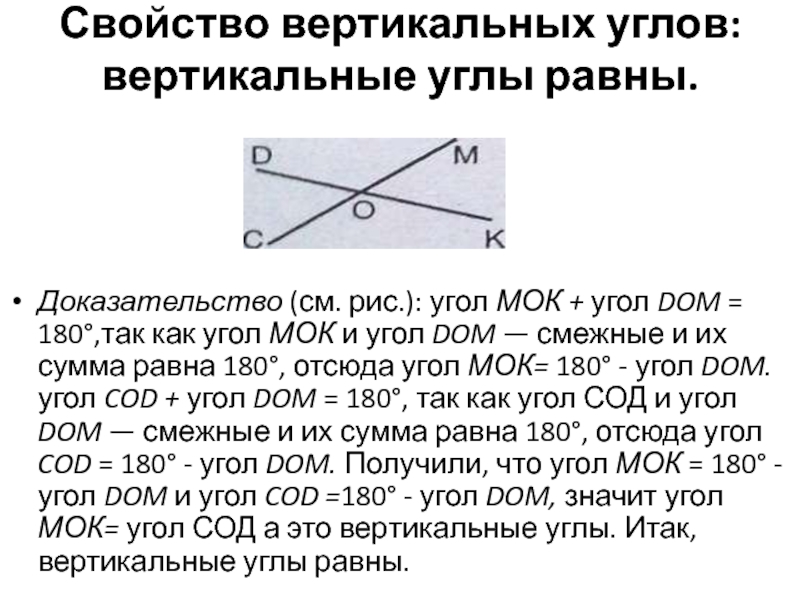
Слайд 6Свойство вертикальных углов: вертикальные углы равны.
Доказательство (см. рис.): угол МОК
+ угол DOM = 180°,так как угол МОК и угол
DOM — смежные и их сумма равна 180°, отсюда угол МОК= 180° - угол DOM. угол COD + угол DOM = 180°, так как угол СОД и угол DOM — смежные и их сумма равна 180°, отсюда угол COD = 180° - угол DOM. Получили, что угол МОК = 180° - угол DOM и угол COD =180° - угол DOM, значит угол МОК= угол СОД а это вертикальные углы. Итак, вертикальные углы равны.Слайд 75) Закрепление изученного материала
Устно решить задачи №41,43,44 из рабочей тетради
и №59, 60, 63 из учебника.
Всем классом решить письменно задачи
№ 62,65(a).Самостоятельное решение задач. № 61 (в,г) ; 64 (а);
6) Итог урока. 7) Домашнее задание
Пункт 11, вопросы №17,18. Задачи №61(б,д) ; 64(б); 65(б).