Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Четыре замечательные точки треугольника. Свойство биссектрисы угла 8 класс
Содержание
- 1. Четыре замечательные точки треугольника. Свойство биссектрисы угла 8 класс
- 2. Теорема Каждая точка биссектрисы неразвернутого угла равноудалена
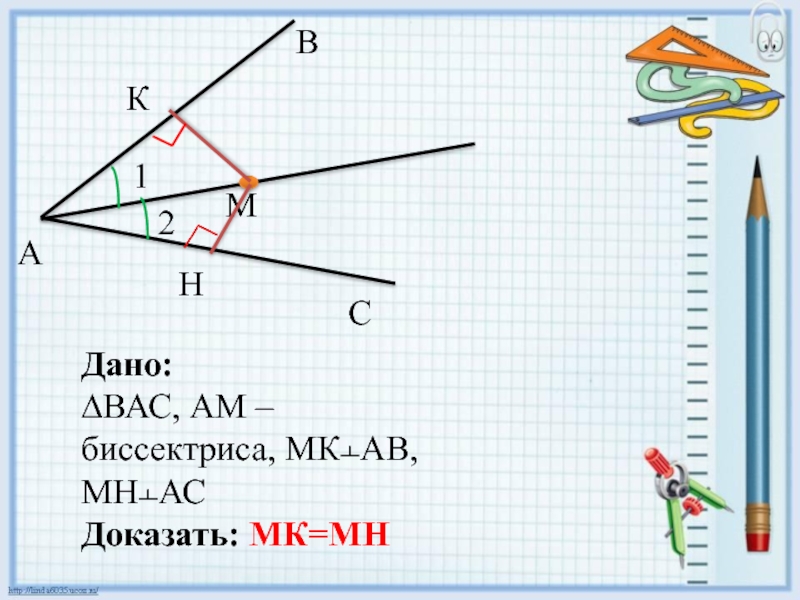
- 3. ВАСМКН12Дано:∆ВАС, АМ – биссектриса, МК﬩АВ, МН﬩АСДоказать: МК=МН
- 4. Рассмотрим ∆АМК и ∆АМН:∟1=∟2 (по условию)АМ –
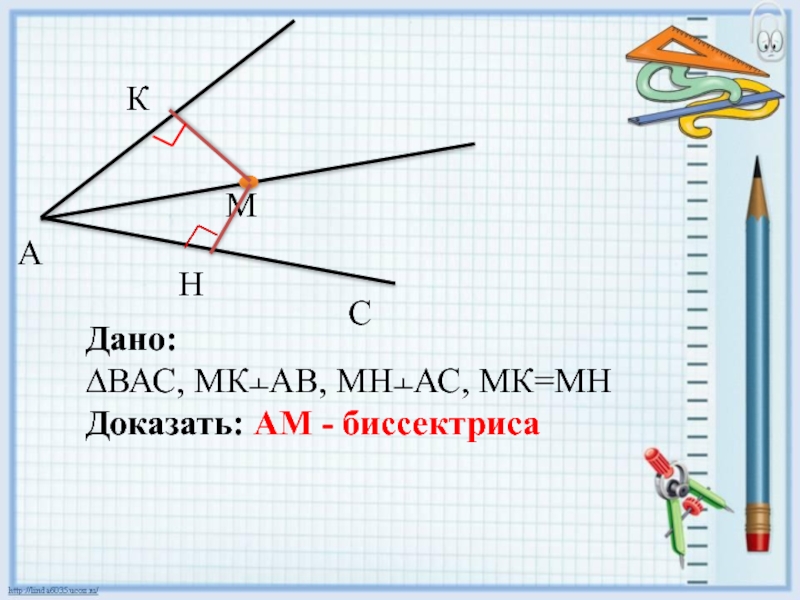
- 5. Дано:∆ВАС, МК﬩АВ, МН﬩АС, МК=МНДоказать: АМ - биссектрисаСА
- 6. Рассмотрим ∆АМК и ∆АМН:МК = МН (по
- 7. Следствие 1. Геометрическим местом точек плоскости, лежащих
- 8. Следствие 2. Биссектрисы треугольника пересекаются в одной точке
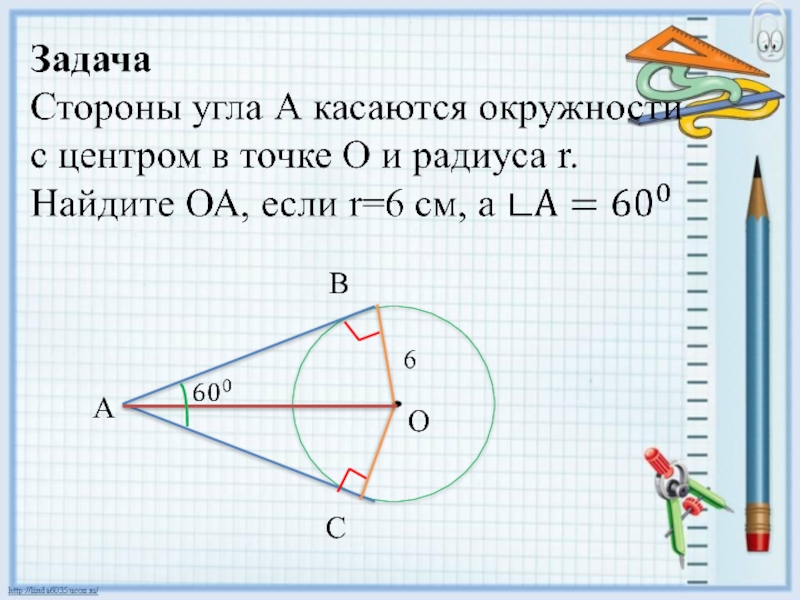
- 9. ОАВС6
- 10. В ВО=ОС=6 см (как радиусы окружности)АВ=АС (как отрезки
- 11. 1) Геометрия: учеб, для
- 12. Скачать презентанцию
Теорема Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. Обратная теорема. Каждая точка , лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе
Слайды и текст этой презентации
Слайд 1Четыре замечательные точки треугольника.
Свойство биссектрисы угла
Учитель математики МБОУ
г. Иркутска
СОШ №38
Слайд 2Теорема Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. Обратная теорема. Каждая
точка , лежащая внутри угла и равноудаленная от сторон угла,
лежит на его биссектрисеСлайд 4Рассмотрим ∆АМК и ∆АМН:
∟1=∟2 (по условию)
АМ – общая гипотенуза
Значит ∆АМК
= ∆АМН (по гипотенузе и острому углу).
Следовательно МК=МН.
Слайд 6Рассмотрим ∆АМК и ∆АМН:
МК = МН (по условию)
АМ – общая
гипотенуза
Значит ∆АМК = ∆АМН (по гипотенузе и катету).
Следовательно АМ
- биссектриса. Слайд 7Следствие 1.
Геометрическим местом точек плоскости, лежащих внутри неразвернутого угла
и равноудаленных от сторон угла, является биссектриса угла.
Слайд 10В
ВО=ОС=6 см (как радиусы окружности)
АВ=АС (как отрезки касательных к окружности,
проведенные из одной точки)
Т.к. т.О равноудалена от сторона угла ВАС,
то луч ОА – биссектриса угла ВАС
Слайд 111) Геометрия: учеб, для 7—9 кл. /
[Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др.]. —
М.: Просвещение, 2004-2008.2) Зив Б.Г. .Геометрия: дидакт. материалы для 8 кл. / Б. Г. Зив, В.М. Мейлер. — М.: Просвещение, 2004—2008.
3) Изучение геометрии в 7, 8, 9 классах: метод, рекомендации: кн. для учителя / [Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др.]. -М.: Просвещение, 2003 — 2008
Список методической литературы