Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аксиомы планиметрии 7 класс
Содержание
- 1. Аксиомы планиметрии 7 класс
- 2. Геометрия ЕвклидаПервым систематическим изложением геометрии, дошедшим до
- 3. В “Началах” был развит
- 4. Аксиомы планиметрии
- 5. Аксиомами называются те основные положения геометрии,
- 6. Основные понятия (фигуры) на плоскости:
- 7. Аксиомы взаимного расположения точек и прямых:1.Каждой прямой
- 8. Аксиомы расположения точек на прямой:4. Из трёх
- 9. Аксиома расположения точек на плоскости:6. Каждая прямая
- 10. Аксиомы наложения или равенства фигур.Наложение – это
- 11. Аксиомы наложения или равенства фигур:7. Если при
- 12. Аксиомы наложения или равенства фигур:10. Любой угол
- 13. Аксиомы наложения или равенства фигур:12.
- 14. Аксиомы измерения отрезков:14. При выбранной единице измерения
- 15. Аксиома параллельных прямых:16. Через точку, не лежащую на данной прямой, проходит только одна прямая параллельная данной.
- 16. Постулаты Евклида1. Из каждой точки ко всякой
- 17. О чем говорится в V постулате Евклида?Если
- 18. Аксиомы планиметрии1.Какова бы ни была прямая, существуют
- 19. Аксиомы планиметрии6.На любой полупрямой от ее начальной
- 20. Скачать презентанцию
Геометрия ЕвклидаПервым систематическим изложением геометрии, дошедшим до нашего времени, являются “Начала” – сочинения александрийского математика Евклида.
Слайды и текст этой презентации
Слайд 1Презентация по геометрии учителя математики МКОУ СОШ №1 пгт. Палана Камчатский край Учебник геометрии 7
– 9.
Авторы: Л.С. Атанасян и другие.
Слайд 2Геометрия Евклида
Первым систематическим изложением геометрии, дошедшим до нашего времени, являются
“Начала” – сочинения александрийского математика Евклида.
Слайд 3 В “Началах” был развит аксиоматический подход к
построению геометрии, который состоит в том, что сначала формулируются основные
положения (аксиомы), а затем на их основе посредством рассуждений доказываются другие утверждения (теоремы).Изложение геометрии Евклидом долгое время служило недосягаемым образцом точности, безукоризненности и строгости.
Только в начале 20 века математики смогли улучшить логические основания геометрии.
«Начала»
Слайд 5 Аксиомами называются те основные положения геометрии, которые принимаются в
качестве исходных.
Или :
Аксиомами называются утверждения, которые принимаются без доказательства.
Слайд 6Основные понятия (фигуры) на плоскости:
точка и прямая
Используя основные понятия и
аксиомы даются определения новых понятий, формулируются и доказываются теоремы о свойствах геометрических фигур.
Слайд 7Аксиомы взаимного расположения точек и прямых:
1.Каждой прямой принадлежит по крайней
мере две точки.
2. Имеются по крайней мере три точки, не
лежащие на одной прямой. 3. Через любые две точки проходит прямая, и притом только одна.
Слайд 8Аксиомы расположения точек на прямой:
4. Из трёх точек прямой одна
и только одна лежит между двумя другими.
5. Каждая точка О
прямой разделяет её на две части(два луча) так, что любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.Слайд 9
Аксиома расположения точек на плоскости:
6. Каждая прямая а разделяет плоскость
на две части (две полуплоскости) так, что любые две точки
одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а.Слайд 10Аксиомы наложения или равенства фигур.
Наложение – это отображение плоскости на
себя.
Если существует наложение, при котором фигура Ф отображается на фигуру
Ф1, то говорят, что фигуру Ф можно совместить наложением с фигурой Ф1, или фигура Ф равна фигуре Ф1.Слайд 11Аксиомы наложения или равенства фигур:
7. Если при наложении совмещаются концы
двух отрезков, то совмещаются и сами отрезки.
8. На любом луче от его начала можно отложить отрезок, равный данному и притом только один. 9. От любого луча в данную полуплоскость можно отложить угол, равный данному неразвёрнутому углу, и притом только один.Слайд 12
Аксиомы наложения или равенства фигур:
10. Любой угол hk можно совместить
наложением с равным ему углом h1k1 двумя способами:
1)так, что луч h совместится с лучом h1, а луч k – с лучом k1; 2) так, что луч k совместится с лучом k1, а луч h – с лучом h1 . 11. Любая фигура равна сама себе.Слайд 13
Аксиомы наложения или равенства фигур:
12. Если фигура Ф
равна фигуре Ф1, то фигура Ф1 равна фигуре Ф.
13. Если
фигура Ф1 равна фигуре Ф2, а фигура Ф2 равна фигуре Ф3, то фигура Ф1 равна фигуре Ф3. Слайд 14Аксиомы измерения отрезков:
14. При выбранной единице измерения отрезков длина каждого
отрезка выражается положительным числом.
Аксиома существования отрезка данной длины:
15. При выбранной
единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом.Слайд 15Аксиома параллельных прямых:
16. Через точку, не лежащую на данной прямой,
проходит только одна прямая параллельная данной.
Слайд 16Постулаты Евклида
1. Из каждой точки ко всякой другой точке можно
провести прямую;
2. Каждую ограниченную прямую можно продолжить неопределённо;
3. Из любого
центра можно описать окружность любого радиуса;4. Все прямые углы равны;
5. И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньше двух прямых, то продолженные эти прямые неограниченно встретятся с той стороны, где углы меньше двух прямых
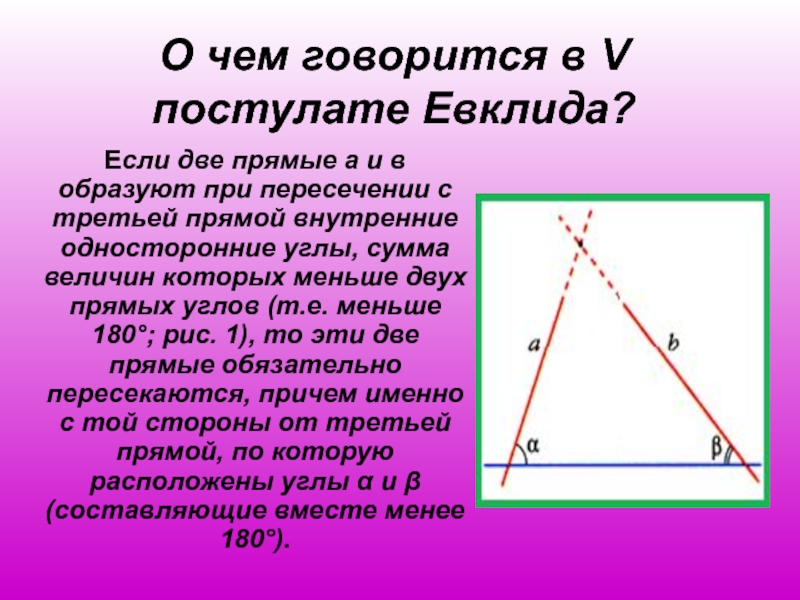
Слайд 17О чем говорится в V постулате Евклида?
Если две прямые а
и в образуют при пересечении с третьей прямой внутренние односторонние
углы, сумма величин которых меньше двух прямых углов (т.е. меньше 180°; рис. 1), то эти две прямые обязательно пересекаются, причем именно с той стороны от третьей прямой, по которую расположены углы α и β (составляющие вместе менее 180°).Слайд 18Аксиомы планиметрии
1.Какова бы ни была прямая, существуют точки, принадлежащие этой
прямой, и точки, не принадлежащие ей. Через любые две точки
можно провести прямую, и только одну.2.Из трех точек на прямой одна и только одна лежит между двумя другими.
3.Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
4.Прямая,принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.
5.Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180.Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом,проходящим между его сторонами.
Слайд 19Аксиомы планиметрии
6.На любой полупрямой от ее начальной точки можно отложить
отрезок заданной длины, и только один.
7.От полупрямой на содержащей ее
плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180,и только один.8.Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
9.На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.