Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сфера и шар
Содержание
- 1. Сфера и шар
- 2. Сфера и шарСферой называется поверхность, состоящая из
- 3. Уравнение сферыС (хº; уº; zº )RМ( х;
- 4. Взаимное расположение сферы и плоскости.Исследуем взаимное расположение
- 5. 1. d < R.Тогда R² - d²
- 6. 2.d = R. Тогда R² - d²
- 7. 3. d > R.Тогда R²- d² <
- 8. Касательная плоскость к сфереПлоскость, имеющая со сферой
- 9. Доказательство: Рассмотрим плоскость α , касающуюся сферы
- 10. Площадь сферыДля определения площади сферы воспользуемся понятием
- 11. Работу выполнила Тулыговец АлёнаУченица 11 класса МКОУ
- 12. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Сфера и шар
1.Уравнение сферы.
2.Взаимное расположение сферы и плоскости.
3.Касательная плоскости к
сфере.
Слайд 2Сфера и шар
Сферой называется поверхность, состоящая из всех точек пространства,
расположенных на данном расстоянии от данной точки.
R
O
Данная точка называется
– центром сферыА данное расстояние – радиусом сферы.
Слайд 3Уравнение сферы
С (хº; уº; zº )
R
М( х; у ;z )
z
x
у
О
Выведем
уравнение сферы радиуса R с центром С (Хº;Уº; Zº; )
Расстояние от произвольной точки М (х; у; z;) до точки С вычисляем по формуле
МС = √(х – х°)² + (у – у°)² + (z – z°)². (1)
Если же точка М лежит на данной сфере, то МС = R, или МС² = R², т. е. координаты точки М удовлетворяют уравнению (х – х°)² + (у – у°)² + (z – z°)² = R² . Если же точка М (х; у; z;) не лежит на данной сфере, МС² = R², т. е. координаты точки М не удовлетворяют уравнению (1).
Следовательно, в прямоугольной системе координат уравнение сферы радиуса R с центром С (хº;уº; zº; ) имеет вид
(х – х°)² + (у – у°)² + (z – z°)² = R² .
Слайд 4Взаимное расположение сферы и плоскости.
Исследуем взаимное расположение сферы и плоскости
в зависимости от соотношения между радиусом сферы и расстоянием от
её центра до плоскости. Обозначим радиус сферы буквой R, а расстояние от её центра до плоскости α − буквой d. Введем систему координат так, как показано на рисунке: плоскость Оху совпадает с плоскостью α, ацентр С сферы лежит на положительной
полуоси Оz. В этой системе координат точка С
имеет координаты (0;0;d), поэтому сфера
имеет уравнение х² + у² + (z – d)² = R².
Плоскость α совпадает с координатной
плоскостью Оху, и поэтому её уравнение имеет
вид z = 0. z = 0 х² + у² + (z – d)² = R². Подставим z = 0 во второе уравнение, получим x² + y² = R² - d². (2) Возможны три случая.
х
α
у
R
O
Слайд 51. d < R.
Тогда R² - d² > 0, и
уравнение (2) является уравнением окружности радиуса r = √R²- d² c
центром в точке О на плоскости Оху. Координаты любой точки М (х; у; 0) этой окружности удовлетворяют как уравнению плоскости α, так и уравнению сферы, т. е. все точки этой окружности являются общими точками плоскости и сферы. Таким образом, в данном случае сфера и плоскость пересекаются по окружности. Итак, если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность. Ясно, что сечение шара плоскостью есть круг. Если секущая плоскость проходит через центр шара, то d = 0 и в сечении получается круг радиуса R, т.е. круг, радиус которого равен радиусу шара. Если секущая плоскость не проходит через центр шара, то d > 0 и радиус сечения r = √R² - d², очевидно, меньше радиуса шара шара.х
α
у
z
R
O
С(0;0;:d)
d < R, r = √R²- d²
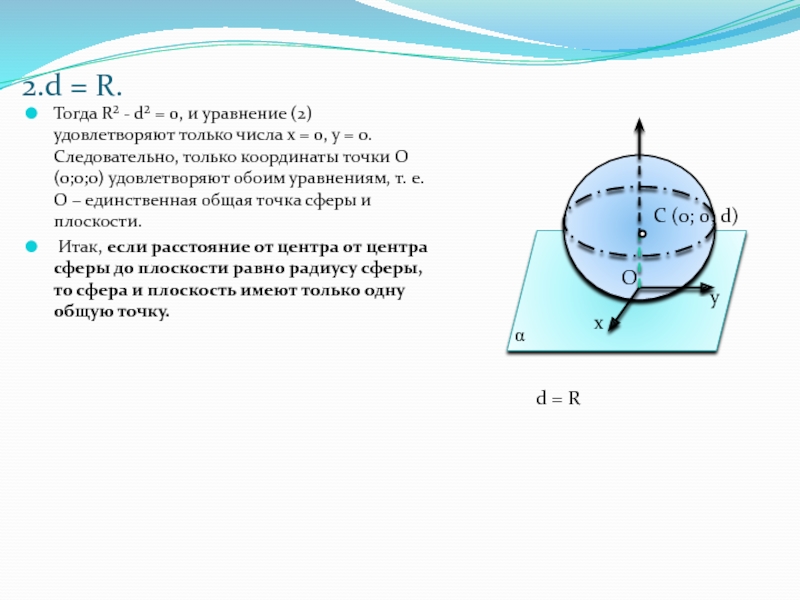
Слайд 62.d = R.
Тогда R² - d² = 0, и
уравнение (2) удовлетворяют только числа х = 0, у = 0.
Следовательно, только координаты точки О (0;0;0) удовлетворяют обоим уравнениям, т. е. О – единственная общая точка сферы и плоскости.Итак, если расстояние от центра от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку.
х
α
у
O
С (0; 0; d)
d = R
Слайд 73. d > R.
Тогда R²- d² < 0, и уравнению
(2) не удовлетворяют координаты никакой точки. Следовательно, если расстояние от центра сферы
до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.х
α
у
O
С (0; 0; d)
z
d > R
Слайд 8Касательная плоскость к сфере
Плоскость, имеющая со сферой только одну общую
точку , называется касательной плоскостью к сфере, а их общая
точка называется точкой касания плоскости и сфере. На рисунке плоскость α касательная к сфере с центром О, А – точка касания.α
О
А
ТЕОРЕМА:
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости .
Слайд 9Доказательство:
Рассмотрим плоскость α , касающуюся сферы с центром О
в точке А. Докажем, что радиус ОА перпендикулярен к плоскости
α. Предположим, что это не так. Тогда радиус ОА является наклонной к плоскости αи, следовательно расстояние от центра сферы до плоскости α
Меньше радиуса сферы. Поэтому сфера и плоскость пересекаются по окружности. Но это противоречит тому, что плоскость α – касательная, т.е. сфера и плоскость α имеют только одну общую точку. Полученное противоречие доказывает, что радиус ОА перпендикулярен к плоскости α. Теорема доказана.
Докажем обратную теорему
α
О
А
ТЕОРЕМА – Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.
Слайд 10Площадь сферы
Для определения площади сферы воспользуемся понятием описанного многогранника. Многогранник
называется описанным около сферы(шара), если сфера касается всех его граней.
При этом сфера называется вписанной в многогранник.На рисунке изображены описанные около сферы тетраэдр и куб. За площадь сферы примем предел последовательности площадей поверхностей этих многогранников.
S = 4πR²
Слайд 11Работу выполнила
Тулыговец Алёна
Ученица 11 класса МКОУ Суминской СОШ
Руководитель: учитель
математики Федоровская З.Д.
2013г.