Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Начальные понятия стереометрии
Содержание
- 1. Начальные понятия стереометрии
- 2. Начальные понятия стереометрииАксиомы и следствия из них
- 3. Вопросы к лекции.1. Когда зародилась наука геометрия?2.
- 4. Евклид – древнегреческий математик
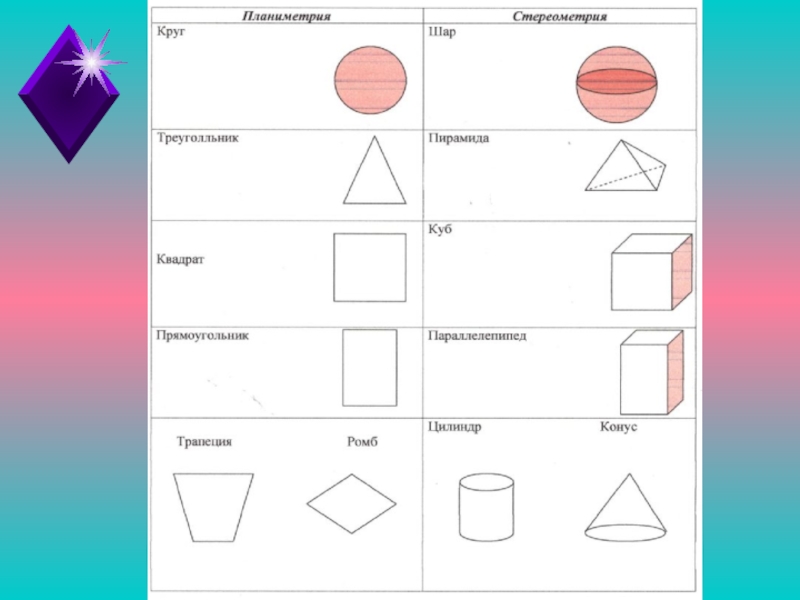
- 5. ГЕОМЕТРИЯПланиметрияСтереометрия
- 6. Планиметрия - это раздел геометрии, который изучает фигуры на плоскости.А стереометрия? Подумай и сформулируй!
- 7. Это раздел геометрии, в котором изучаются фигуры, расположенные в пространстве.Шар èßПирамидаКубèПлоскостьèçПрямая
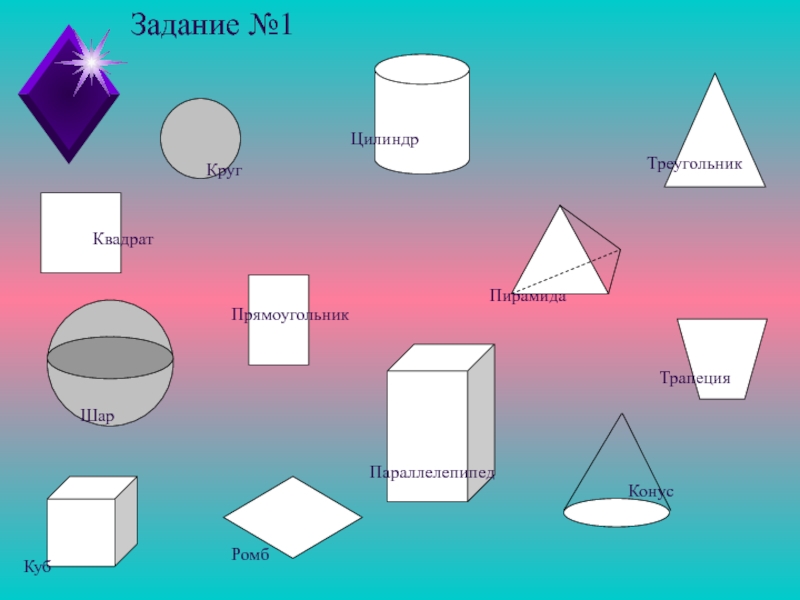
- 8. Задание №1ЦилиндрПирамидаРомбКонусПрямоугольникТреугольникШарТрапецияПараллелепипедКвадратКубКруг
- 9. Слайд 9
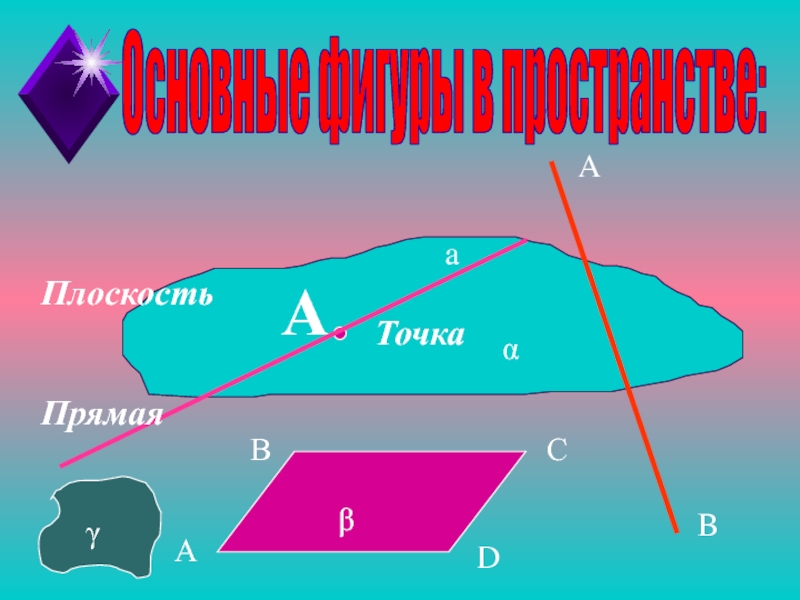
- 10. ПлоскостьАТочкаПрямаяaABОсновные фигуры в пространстве:α β АВСDγ
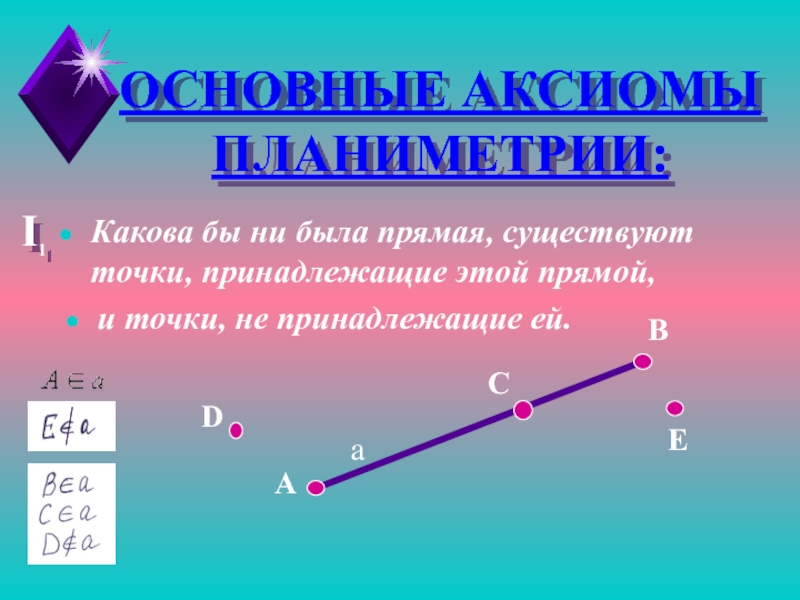
- 11. ОСНОВНЫЕ АКСИОМЫ ПЛАНИМЕТРИИ:I1Какова бы ни была прямая,
- 12. I2Через любые две точки можно провести прямую, и только одну.ОСНОВНЫЕ АКСИОМЫ ПЛАНИМЕТРИИ:
- 13. ОСНОВНЫЕ АКСИОМЫ СТЕРЕОМЕТРИИ:С1Какова бы ни была плоскость,
- 14. ОСНОВНЫЕ АКСИОМЫ СТЕРЕОМЕТРИИ:С2Если две различные плоскости имеют
- 15. ОСНОВНЫЕ АКСИОМЫ СТЕРЕОМЕТРИИ:С3Если две различные прямые имеют
- 16. Теорема 1.Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
- 17. Доказательство:Пусть а - данная прямая, и В
- 18. Проведем через точки А и В прямую b (аксиома I2)Доказательство:b
- 19. Прямые а и b различны, Доказательство:аbтак как
- 20. Проведем через прямые а и b плоскость
- 21. Докажем теперь, что плоскость a ,Доказательство: проходящая
- 22. По аксиоме С2 плоскости a и a1
- 23. Но точка B ,общая для плоскостей a
- 24. Теорема 2.Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.
- 25. Теорема 3.Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
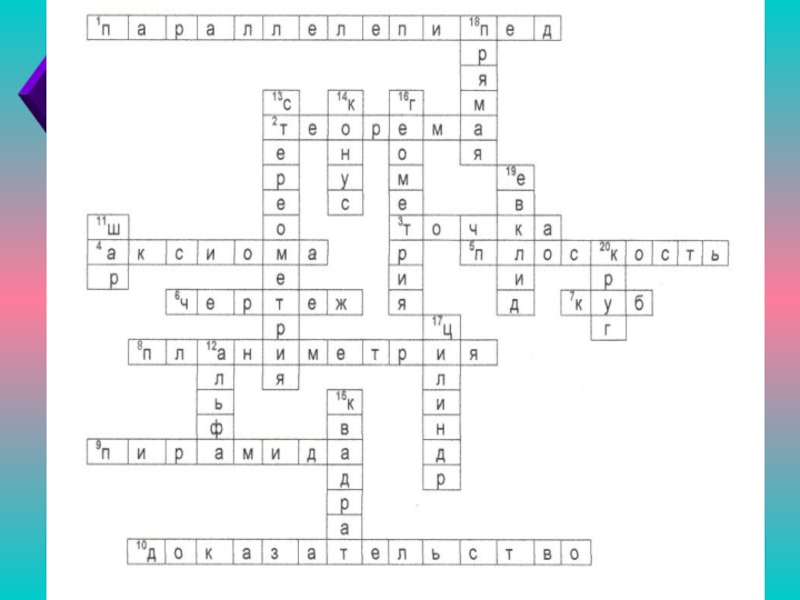
- 26. Задание №3
- 27. Слайд 27
- 28. Слайд 28
- 29. Задание № 4. В пространстве
- 30. Итак, подведем итоги:1. Когда зародилась наука геометрия?2.
- 31. Домашнее задание Выучить опорный конспект.Доказать теорему 2, теорему 3.Литература:Л.С.Атанасян. Геометрия, учебник для 10-11 классов.
- 32. Спасибо за внимание!
- 33. Скачать презентанцию
Начальные понятия стереометрииАксиомы и следствия из них
Слайды и текст этой презентации
Слайд 1Раздел: Стереометрия.
К урокам по стереометрии
учителя математики
Варавва Н.А.
МБОУ гимназия
№ 72 имени академика В.П.Глушко города Краснодара
Слайд 3Вопросы к лекции.
1. Когда зародилась наука геометрия?
2. Что означает слово
«геометрия»?
3. Какой ученый первым отразил геометрические понятия в своих сочинениях?
4.
Как Вы понимаете, что такое аксиомы?5. Что такое теоремы в Вашем понятии?
6. На какие разделы делится школьный курс геометрии?
7. Что изучает планиметрия?
8. Что изучает стереометрия?
9. Какие фигуры являются основными в пространстве, как они обозначаются?
10. Аксиомы планиметрии.
11. Аксиомы стереометрии.
12. Сформулируйте теоремы – следствия из аксиом стереометрии.
Слайд 6Планиметрия - это раздел геометрии, который изучает фигуры на плоскости.
А
стереометрия?
Подумай и сформулируй!
Слайд 7 Это раздел геометрии, в котором изучаются фигуры, расположенные в
пространстве.
Шар è
ßПирамида
Кубè
Плоскостьè
çПрямая
Слайд 8Задание №1
Цилиндр
Пирамида
Ромб
Конус
Прямоугольник
Треугольник
Шар
Трапеция
Параллелепипед
Квадрат
Куб
Круг
Слайд 11ОСНОВНЫЕ АКСИОМЫ ПЛАНИМЕТРИИ:
I1
Какова бы ни была прямая, существуют точки, принадлежащие
этой прямой,
А
B
С
и точки, не принадлежащие ей.
a
Слайд 13ОСНОВНЫЕ АКСИОМЫ СТЕРЕОМЕТРИИ:
С1
Какова бы ни была плоскость, существуют точки, принадлежащие
ей,
и точки, не принадлежащие ей:
α
Слайд 14ОСНОВНЫЕ АКСИОМЫ СТЕРЕОМЕТРИИ:
С2
Если две различные плоскости имеют общую точку, то
они пересекаются по прямой, проходящей через эту точку:
K
Слайд 15ОСНОВНЫЕ АКСИОМЫ СТЕРЕОМЕТРИИ:
С3
Если две различные прямые имеют общую точку, то
через них можно провести плоскость, и притом только одну:
S
Слайд 16Теорема 1.
Через прямую и не лежащую на ней точку можно
провести плоскость, и притом только одну.
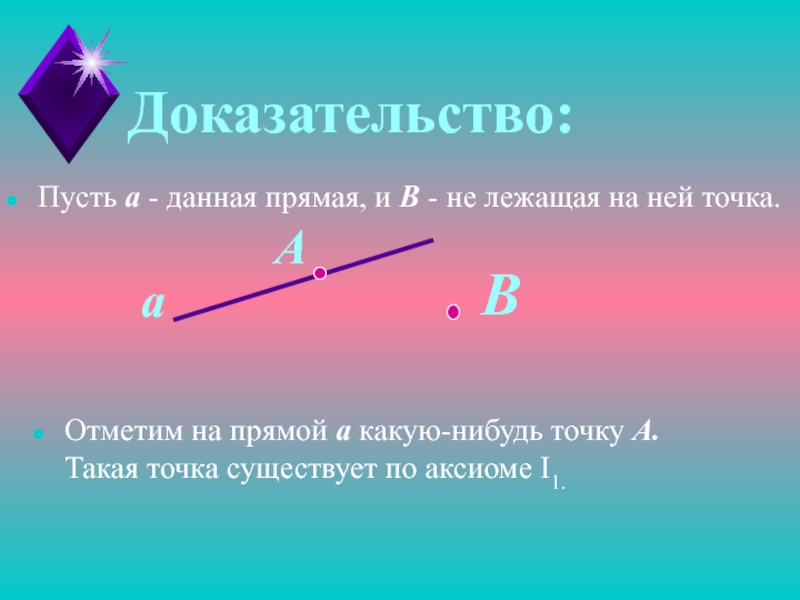
Слайд 17Доказательство:
Пусть а - данная прямая, и В - не лежащая
на ней точка.
а
Отметим на прямой а какую-нибудь точку А. Такая
точка существует по аксиоме I1.
Слайд 19Прямые а и b различны,
Доказательство:
а
b
так как точка B прямой
b
не лежит на прямой а.
Прямые а и b имеют общую
точку А.
Слайд 20Проведем через прямые а и b плоскость a (аксиома С3).
Доказательство:
Эта плоскость проходит через прямую а и точку B.
Слайд 21Докажем теперь, что плоскость a ,
Доказательство:
проходящая через прямую а
а
и точку B,
b
единственна .
Допустим, что существует другая,
отличная от a , плоскость a1 проходящая через прямую а и точку B.
Слайд 22По аксиоме С2 плоскости a и a1 , будучи различными,
пересекаются по прямой, а именно по прямой а .
Доказательство:
а
Следовательно, любая
общая точка плоскостей a и a1 лежит на прямой а .b
Слайд 23Но точка B ,
общая для плоскостей a и a1 ,
заведомо не лежит на прямой а . Получили противоречие. Теорема
доказана.а
Доказательство:
Слайд 24Теорема 2.
Если две точки прямой принадлежат плоскости, то и вся
прямая принадлежит этой плоскости.
Слайд 25Теорема 3.
Через три точки, не лежащие на одной прямой, можно
провести плоскость, и притом только одну.
Слайд 29Задание № 4.
В пространстве задан куб.
Каким плоскостям (граням)
принадлежит точка (вершина) А?
По какой прямой пересекаются плоскости AA1D1D
и ABCD?
Слайд 30Итак, подведем итоги:
1. Когда зародилась наука геометрия?
2. Что означает слово
«геометрия»?
3. Какой ученый первым отразил геометрические понятия в своих сочинениях?
4.
Как Вы понимаете, что такое аксиомы?5. Что такое теоремы в Вашем понятии?
6. На какие разделы делится школьный курс геометрии?
7. Что изучает планиметрия?
8. Что изучает стереометрия?
9. Какие фигуры являются основными в пространстве, как они обозначаются?
10. Аксиомы планиметрии.
11. Аксиомы стереометрии.
12. Сформулируйте теоремы – следствия из аксиом стереометрии.
Слайд 31Домашнее задание
Выучить опорный конспект.
Доказать теорему 2, теорему 3.
Литература:
Л.С.Атанасян. Геометрия,
учебник для 10-11 классов.
