Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Перпендикуляр к прямой 7 класс
Содержание
Слайды и текст этой презентации
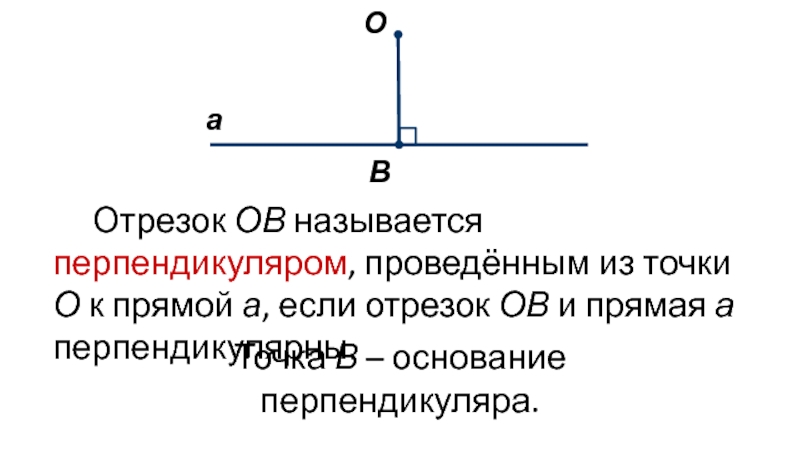
Слайд 2Отрезок ОВ называется перпендикуляром, проведённым из точки О к прямой
а, если отрезок ОВ и прямая а перпендикулярны.
основание перпендикуляра.Слайд 3Доказательство.
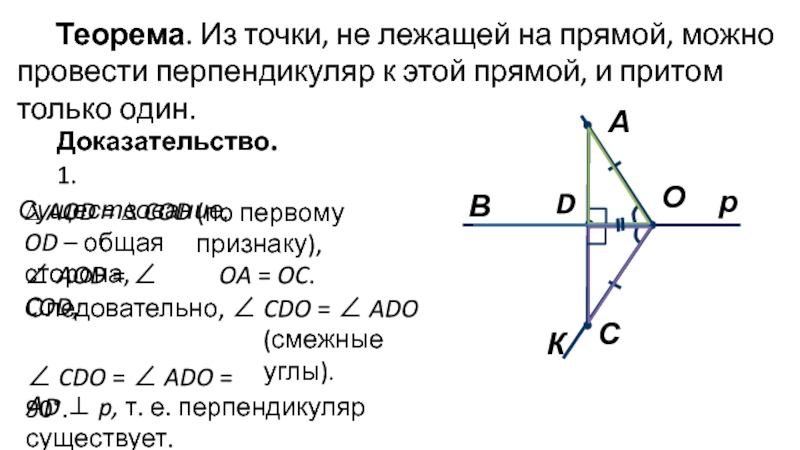
1. Существование.
Теорема. Из точки, не лежащей на прямой, можно
провести перпендикуляр к этой прямой, и притом только один.
∠
AOD = ∠ COD, OA = OC.
Следовательно, ∠ CDO = ∠ ADO
(смежные углы).
АD ⊥ p, т. е. перпендикуляр существует.
(по первому признаку),
Слайд 4AD = CD,
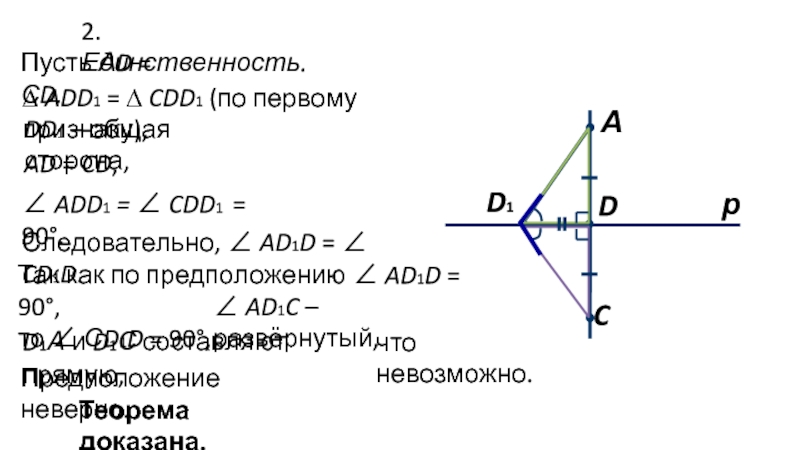
Так как по предположению ∠ AD1D =
90°,
то ∠ СD1D = 90°,
D1А и D1С составляют прямую,
что невозможно.
Предположение
неверно.Теорема доказана.
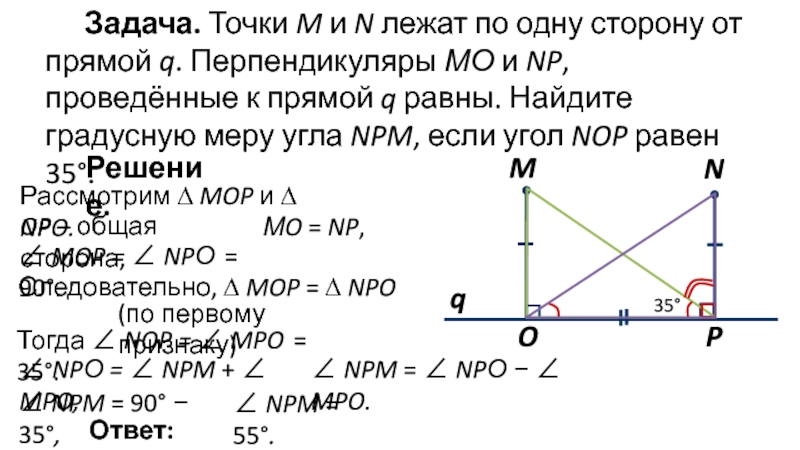
Слайд 6Задача. Точки M и N лежат по одну сторону от
прямой q. Перпендикуляры МО и NP, проведённые к прямой q
равны. Найдите градусную меру угла NPM, если угол NOP равен 35°.Рассмотрим ∆ MOP и ∆ NPO.
Решение.
OP – общая сторона,
МO = NP,
∠ MOP = ∠ NPО = 90°.
Следовательно, ∆ MOP = ∆ NPO
(по первому признаку)
Тогда ∠ NOP = ∠ MPO = 35°.
∠ NPО = ∠ NPM + ∠ MPO,
∠ NPM = ∠ NPО ∠ MPO.
35°
∠ NPM = 90° 35°,
∠ NPM = 55°.
Ответ: 55°.