Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач на применение аксиом стереометрии и их следствий
Содержание
- 1. Решение задач на применение аксиом стереометрии и их следствий
- 2. Данная презентация посвящена аксиомам стереометрии и следствиям
- 3. Решение задач на применение аксиом стереометрии и
- 4. Цель урока:Закрепить усвоение вопросов теории в процессе
- 5. Ход урокаΙ. Организационный момент.ΙΙ. Устная работа.
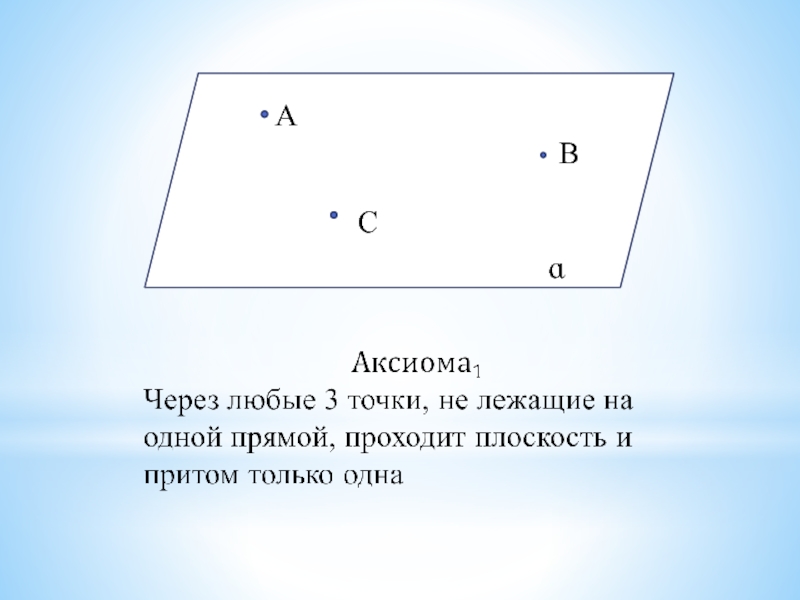
- 6. П о в т о р я е мКаковы аксиомы стереометрии?
- 7. АВСɑ
- 8. Верно ли, что:Любые три точки лежат в одной плоскости;ДаЛюбые четыре точки лежат в одной плоскости;Нет
- 9. Любые четыре точки не лежат в одной
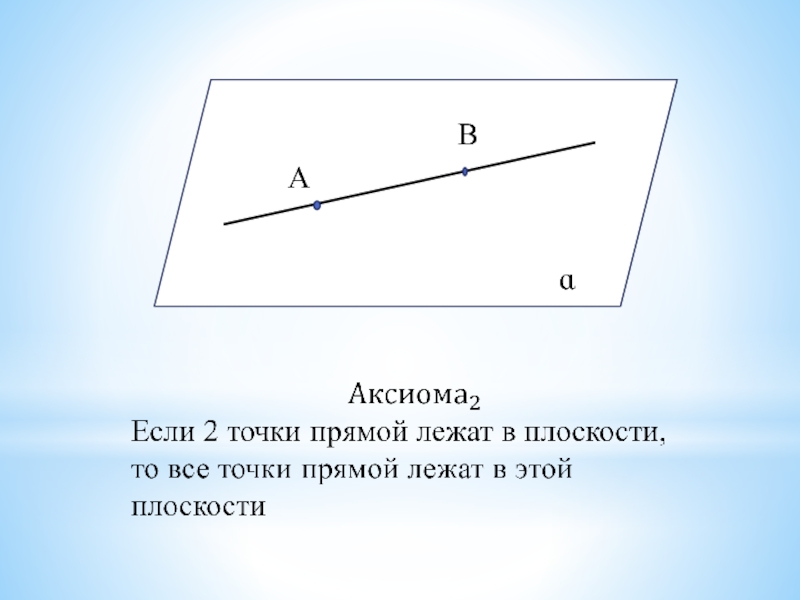
- 10. АВɑ
- 11. Верно ли, что прямая лежит в плоскости
- 12. Ааɑß
- 13. АДВСКМНазовите плоскости, в которых лежат точка К, точка М.
- 14. Каковы следствия из аксиом?
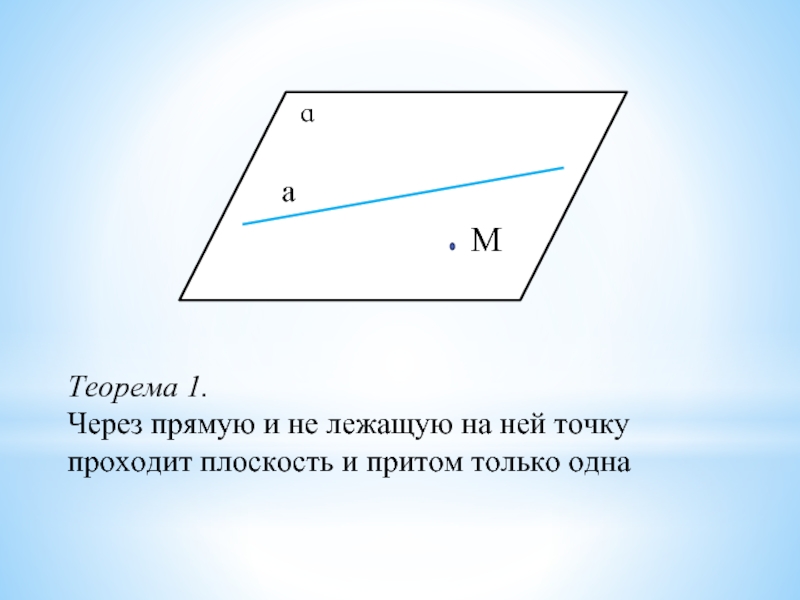
- 15. ɑаМТеорема 1.Через прямую и не лежащую на ней точку проходит плоскость и притом только одна
- 16. асɑТеорема 2.Через 2 пересекающиеся прямые проходит плоскость, и притом только одна
- 17. ΙΙΙ. Решение задач на готовом чертеже
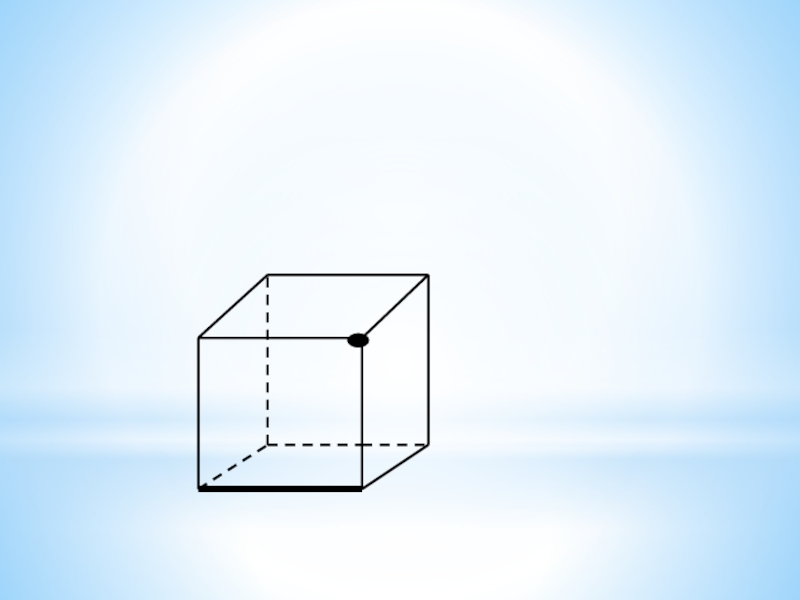
- 18. Сколько плоскостей можно провести через выделенные элементы куба?Заштрихуйте соответствующие плоскостям грани куба.
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Сколько граней проходит через:а) одну,б) две,в) три,г)
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Ι\/. Самостоятельная работа контролирующего характераОценка «3» –
- 32. 1.Какое из следующих утверждений верно?а) любые четыре
- 33. 2. Сколько общих точек могут иметь две
- 34. 3. Точки А, В, С лежат на
- 35. 4. Если три точки не лежат на
- 36. 5. Выберите верное утверждение:а) если одна точка
- 37. 6. Назовите общую прямую плоскостей РВМ и
- 38. 8. Две плоскости пересекаются по прямой с.
- 39. 9. Прямые а и в пересекаются в
- 40. 10. Точки А, В, С не лежат
- 41. \/. Подведение итогов.1.Собрать тетради с самостоятельной работой.2.Оценки
- 42. Спасибо за урок
- 43. Скачать презентанцию
Данная презентация посвящена аксиомам стереометрии и следствиям из них.Может быть использована: в виде диагностики знаний обучающихся при завершении темы «Аксиомы стереометрии и следствия из них»;при организации работы по готовому чертежу, что
Слайды и текст этой презентации
Слайд 1
Презентация урока по геометрии
Тема: «Решение задач на применение аксиом стереометрии
и их следствий»
Слайд 2Данная презентация посвящена аксиомам стереометрии и следствиям из них.
Может быть
использована:
в виде диагностики знаний обучающихся при завершении темы «Аксиомы
стереометрии и следствия из них»;при организации работы по готовому чертежу, что способствует развитию быстрого интуитивного логического мышления;
для развития устной и письменной математической речи.
Слайд 3Решение задач на применение аксиом стереометрии и их следствий
Выполнила:
Соломина
Наталья Васильевна
преподаватель математики и информатики
ГБПОУ «Вышневолоцкий медицинский колледж»
Слайд 4Цель урока:
Закрепить усвоение вопросов теории в процессе решения;
Проверить уровень подготовленности
обучающихся:
- при решении задач на готовом чертеже;
- путём
проведения самостоятельной работы контролирующего характера
Слайд 8Верно ли, что:
Любые три точки лежат в одной плоскости;
Да
Любые четыре
точки лежат в одной плоскости;
Нет
Слайд 9Любые четыре точки не лежат в одной плоскости;
Нет
Через любые три
точки проходит плоскость, и притом только одна?
Нет
Слайд 11Верно ли, что прямая лежит в плоскости данного треугольника, если
она ( ответ обоснуйте):
пересекает две стороны треугольника;
проходит через одну из
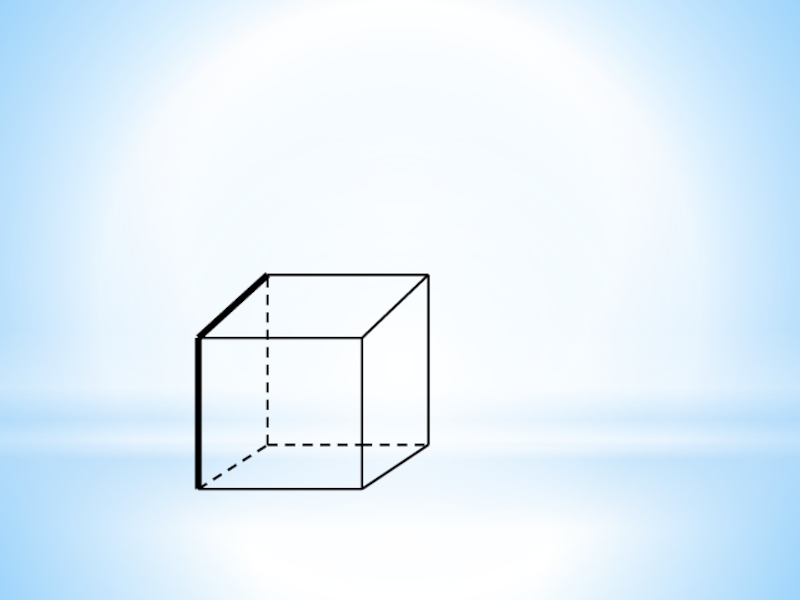
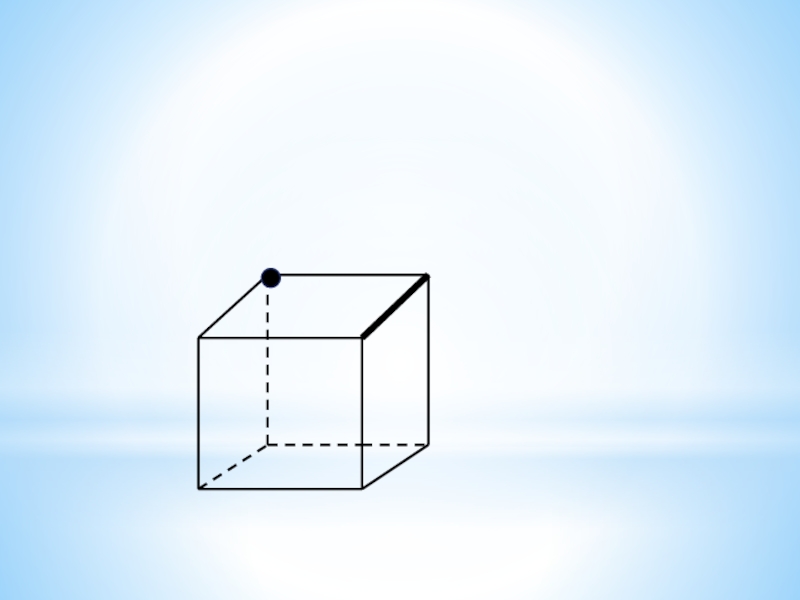
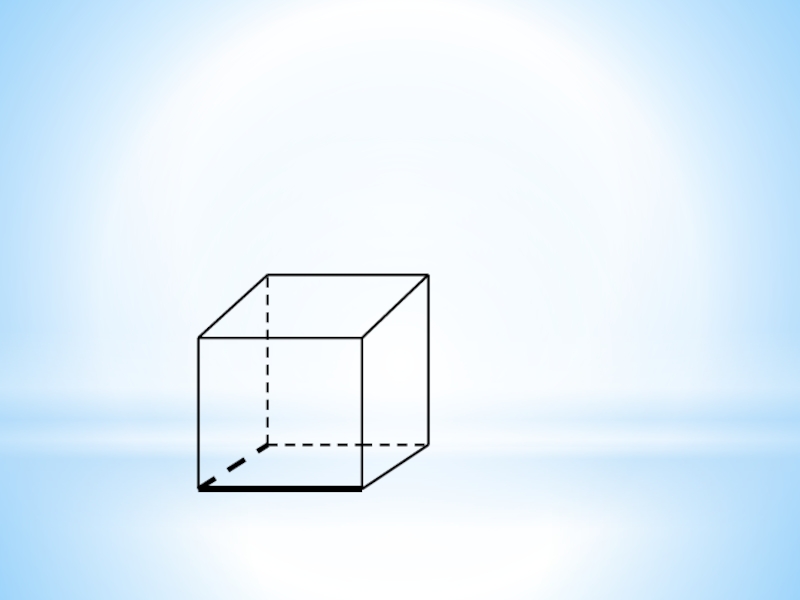
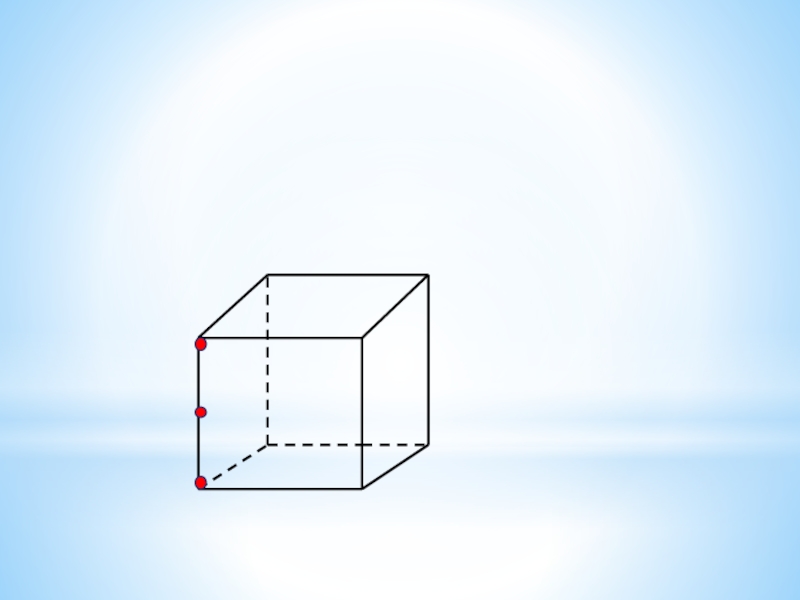
вершин треугольника? 
Слайд 18Сколько плоскостей можно провести через выделенные элементы куба?
Заштрихуйте соответствующие плоскостям
грани куба.
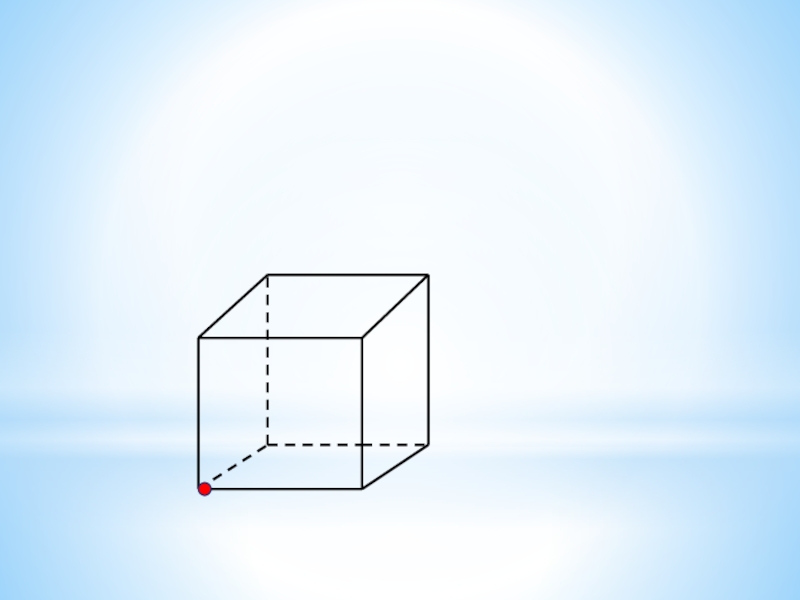
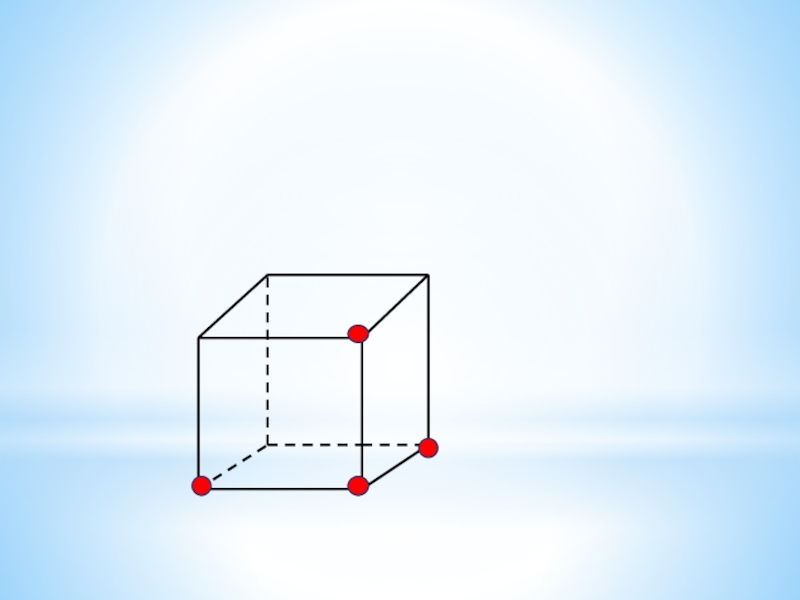
Слайд 24Сколько граней проходит через:
а) одну,
б) две,
в) три,
г) четыре точки, выделенные
на рисунке куба?
Сколько плоскостей можно провести через те же точки?
Определится ли при этом положение плоскости однозначно? Ответ обоснуйте.
Слайд 31Ι\/. Самостоятельная работа контролирующего характера
Оценка «3» – пять любых заданий
Оценка
«4» – семь любых заданий
Оценка «5» – девять любых заданий
Слайд 321.Какое из следующих утверждений верно?
а) любые четыре точки лежат в
одной плоскости;
б) любые три точки не лежат в одной плоскости;
в)
любые четыре точки не лежат в одной плоскости;г) через любые три точки проходит плоскость;
д) через любые три точки проходит плоскость, и притом только одна.
Д
Слайд 332. Сколько общих точек могут иметь две различные плоскости?
а) 2;
б) 3; в) несколько;
г) бесконечно много;д) бесконечно много или ни одной.
Д
Слайд 343. Точки А, В, С лежат на одной прямой, точка
Д не лежит на ней. Через каждые три точки проведена
одна плоскость. Сколько различных плоскостей при этом получилось?а) 2; б) 3; в) 1; г) 4; д) бесконечно много.
В
Слайд 354. Если три точки не лежат на одной прямой, то
положение плоскости в пространстве они:
а) не определяют в любом случае;
б)
определяют, но при дополнительных условиях;в) определяют в любом случае;
г) ничего сказать нельзя;
д) другой ответ.
В
Слайд 365. Выберите верное утверждение:
а) если одна точка прямой лежит в
плоскости, то все точки прямой лежат в этой плоскости;
б) через
прямую и не лежащую на ней точку проходит плоскость, и притом только одна;в) через две пересекающиеся прямые плоскость провести нельзя;
г) любые две плоскости не имеют общих точек;
д) если четыре точки не лежат в одной плоскости, то какие-нибудь три из них лежат на одной прямой.
Б
Слайд 376. Назовите общую прямую плоскостей РВМ и МАВ:
а) РМ;
б) АВ; в) РВ; г) ВМ; д) определить нельзя.
Г
В
С
А
Д
Р
М
Слайд 388. Две плоскости пересекаются по прямой с. Точка М лежит
только в одной из плоскостей. Что можно сказать о взаимном
положении точки М и прямой с?а) никакого вывода нельзя сделать;
б) на прямой с лежит точка М;
в) через точку М прямая с не проходит;
г) другой ответ.
Г
Слайд 399. Прямые а и в пересекаются в точке М. Прямая
с, не проходящая через точку М, пересекает прямые а и
в. Что можно сказать о взаимном положении прямых а, в и с?а) все прямые лежат в разных плоскостях;
б) прямые а и в лежат в одной плоскости, а прямая с в ней не лежит;
в) все прямые лежат в одной плоскости;
г) ничего сказать нельзя;
д) прямая с совпадает с одной из прямых: или са, или св.
В
Слайд 4010. Точки А, В, С не лежат на одной прямой.
МϵАВ, КϵАС, ХϵМК. Выберите верное утверждение:
а) ХϵАВ, б)
ХϵАС, в) ХϵАВС;г) точки Х и М совпадают; д) точки Х, К совпадают
В
Слайд 41\/. Подведение итогов.
1.Собрать тетради с самостоятельной работой.
2.Оценки за урок.
\/Ι.
Домашнее задание.
Постройте изображение тетраэдра (треугольной призмы, четырёхугольной пирамиды, четырёхугольной призмы).
Отметьте произвольно точки М, Н, К на рёбрах многогранника. Постройте сечение многогранника плоскостью (МНК).
