Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы 8 класс
Содержание
- 1. Векторы 8 класс
- 2. Понятие вектораПусть на тело действует сила в
- 3. Понятие вектораРассмотрим произвольный отрезок. На нем можно
- 4. Понятие вектораНа рисунках вектор изображается отрезком со стрелкойВектор АВ, А – начало вектора, В – конец. CD EF LKАВАВCDEFKL
- 5. Понятие вектораВекторы часто обозначают и одной строчной
- 6. Понятие вектораДлиной или модулем ненулевого вектора АВ
- 7. Коллинеарные векторыНенулевые векторы называются коллинеарными, если они
- 8. Равенство векторовОпределение. Векторы называются равными,
- 9. Откладывание вектора от данной точкиЕсли точка А
- 10. Сумма двух векторовРассмотрим пример: Петя из
- 11. Сумма двух векторовПравило треугольника Пусть а
- 12. Законы сложения векторов1) а+b=b+a (переместительный закон) Правило
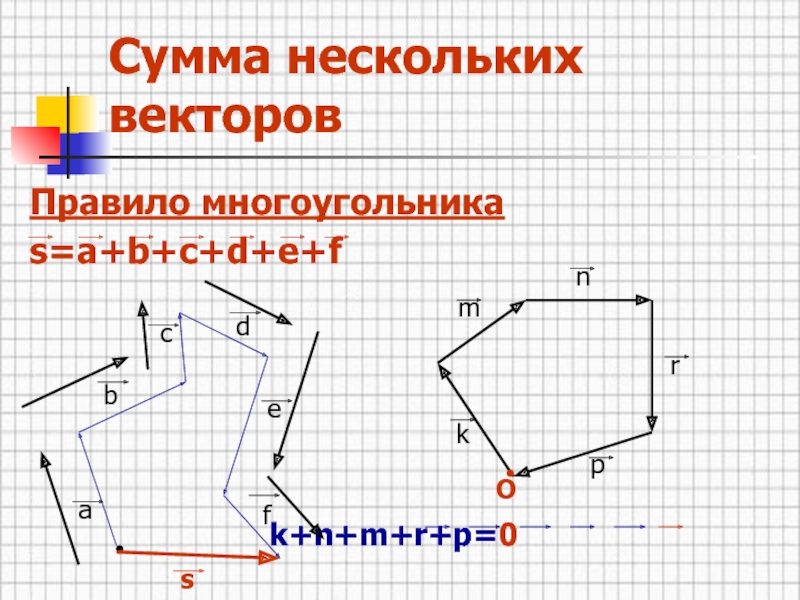
- 13. Сумма нескольких векторовПравило многоугольникаs=a+b+c+d+e+f k+n+m+r+p=0 abcdefskmnrpO
- 14. Противоположные векторы Пусть
- 15. Вычитание векторов Определение.
- 16. Умножение вектора на число
- 17. Умножение вектора на число Для любых чисел
- 18. Скачать презентанцию
Понятие вектораПусть на тело действует сила в 8Н. Стрелка указывает направление силы, а длина отрезка соответствует числовому значению силы.8Н
Слайды и текст этой презентации
Слайд 1 Векторы
Понятие вектора
Равенство векторов
Откладывание вектора от данной точки
Сумма
двух векторов
число
Слайд 2Понятие вектора
Пусть на тело действует сила в 8Н. Стрелка указывает
направление силы, а длина отрезка соответствует числовому значению силы.
8Н
Слайд 3Понятие вектора
Рассмотрим произвольный отрезок. На нем можно указать два направления.
Чтобы выбрать одно из направлений, один конец
отрезка назовем НАЧАЛОМ, а другой – КОНЦОМ и будем считать, что отрезок направлен от начала к концу.Определение.
Отрезок, для которого указано, какой из его концов считается началом, а какой - концом, называется направленным отрезком или вектором.
Слайд 4Понятие вектора
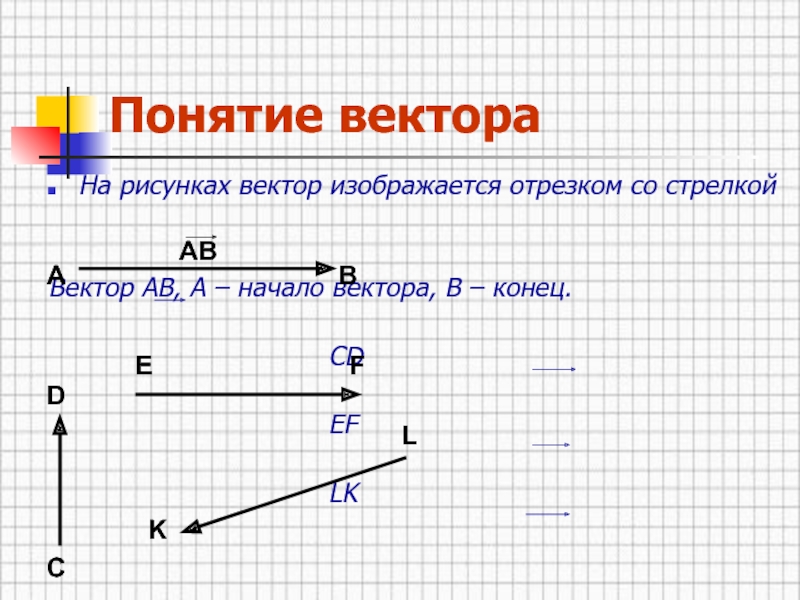
На рисунках вектор изображается отрезком со стрелкой
Вектор АВ, А
– начало вектора, В – конец.
CD
EF
LK
А
В
АВ
C
D
E
F
K
L
Слайд 5Понятие вектора
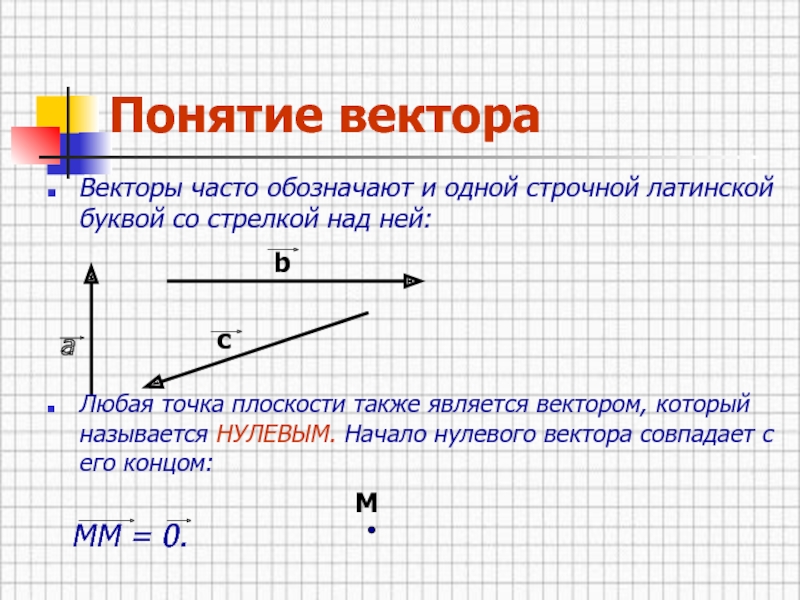
Векторы часто обозначают и одной строчной латинской буквой со
стрелкой над ней:
Любая точка плоскости также является вектором, который называется
НУЛЕВЫМ. Начало нулевого вектора совпадает с его концом: ММ = 0.
a
b
c
М
Слайд 6Понятие вектора
Длиной или модулем ненулевого вектора АВ называется длина отрезка
АВ:
АВ = а = АВ = 5
с = 17
Длина нулевого вектора считается равной нулю:
ММ = 0.
a
М
В
А
с
Слайд 7Коллинеарные векторы
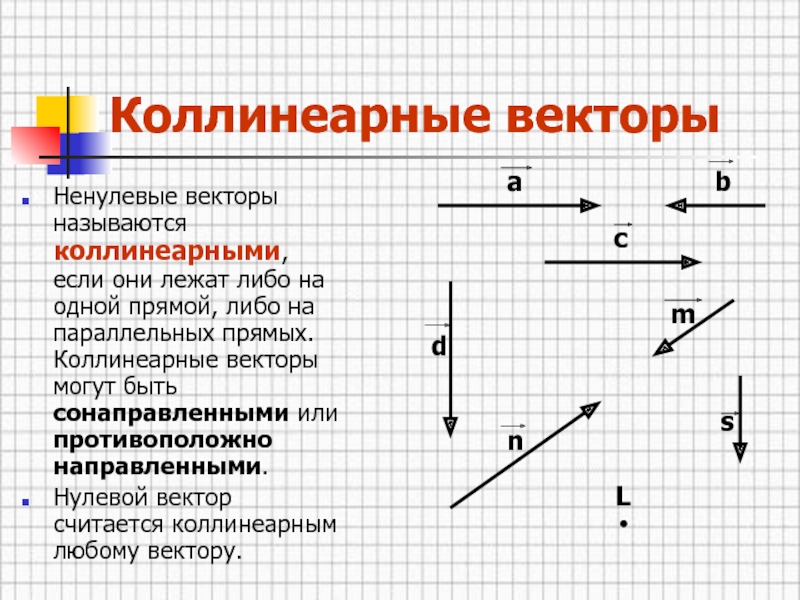
Ненулевые векторы называются коллинеарными, если они лежат либо на
одной прямой, либо на параллельных прямых. Коллинеарные векторы могут быть
сонаправленными или противоположно направленными.Нулевой вектор считается коллинеарным любому вектору.
а
b
c
d
m
n
s
L
Слайд 8Равенство векторов
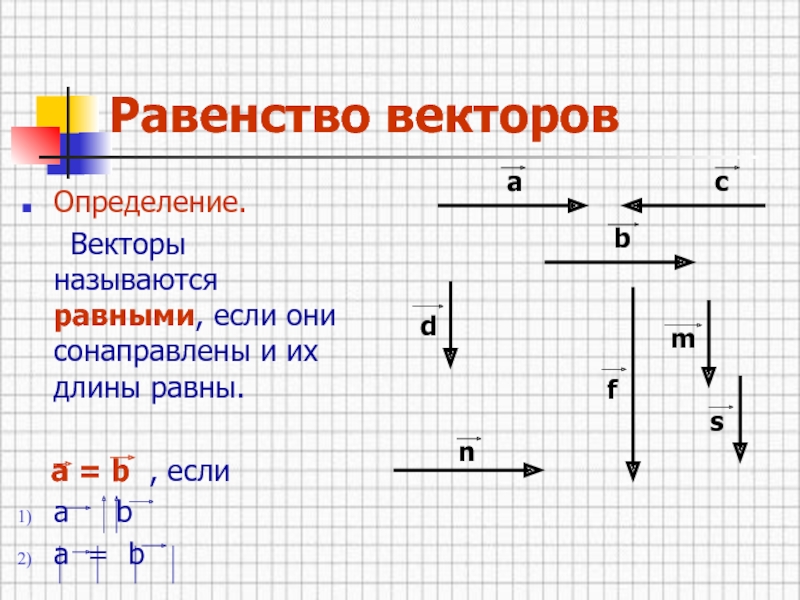
Определение.
Векторы называются равными, если они сонаправлены
и их длины равны.
а = b , если
а
bа = b
а
c
b
d
m
n
s
f
Слайд 9Откладывание вектора от данной точки
Если точка А – начало вектора
а , то говорят, что вектор а отложен от точки
А.Утверждение: От любой точки М можно отложить вектор, равный данному вектору а, и притом только один.
Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой
А
а
М
а
Слайд 10Сумма двух векторов
Рассмотрим пример:
Петя из дома(D) зашел к
Васе(B), а потом поехал в кинотеатр(К).
В результате
этих двух перемещений, которые можно представить векторами DB и BK, Петя переместился из точки D в К, т.е. на вектор DК:DK=DB+BK.
Вектор DK называется суммой векторов DB и BK.
D
B
K
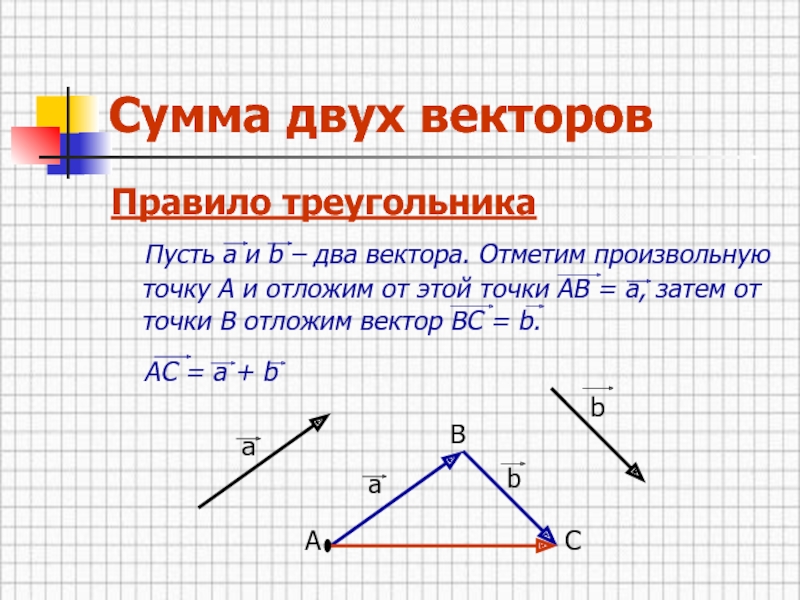
Слайд 11Сумма двух векторов
Правило треугольника
Пусть а и b –
два вектора. Отметим произвольную точку А и отложим от этой
точки АВ = а, затем от точки В отложим вектор ВС = b.АС = а + b
a
b
A
a
b
B
C
Слайд 12Законы сложения векторов
1) а+b=b+a (переместительный закон) Правило параллелограмма
Пусть
а и b – два вектора. Отметим произвольную точку А
и отложим от этой точки АВ = а, затем вектор АD = b. На этих векторах построим параллелограмм АВСD.АС = АВ + BС = а+b
АС = АD + DС = b+a
2) (а+b)+c=a+(b+c)
(сочетательный закон)
a
a
b
b
A
D
C
B
a
b
Слайд 14Противоположные векторы
Пусть а – произвольный
ненулевой вектор.
Определение. Вектор b называется противоположным вектору а, если а
и b имеют равные длины и противоположно направлены.a = АВ, b = BA
Вектор, противоположный вектору c, обозначается так: -c.
Очевидно, с+(-с)=0 или АВ+ВА=0
А
B
a
b
c
-c
Слайд 15Вычитание векторов
Определение. Разностью двух векторов
а и b называется такой вектор, сумма которого с вектором
b равна вектору а.Теорема. Для любых векторов а и b справедливо равенство а - b = а + (-b).
Задача. Даны векторы а и b. Построить вектор а – b.
а
а
b
-b
-b
a - b
Слайд 16Умножение
вектора на число
Определение. Произведением
ненулевого вектора а на число k называется такой вектор b,
длина которого равна вектору k а , причем векторы а и b сонаправлены при k≥0 ипротивоположно направлены при k<0.
Произведением нулевого вектора на любое число считается нулевой вектор.
Для любого числа k и любого вектора а векторы а и ka коллинеарны.
а
-2a
3а
Слайд 17Умножение
вектора на число
Для любых чисел k, n и любых
векторов а, b справедливы равенства:
(kn) а = k (na) (сочетательный
закон) (k+n) а = kа + na (первый распределительный закон)
K ( а+ b ) = kа + kb (второй распределительный закон)
Свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например,
p = 2( a – b) + ( c + a ) – 3( b – c + a ) =
= 2a – 2b + c + a – 3b + 3c – 3a = - 5b + 4c
