Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Пифагора и ее применение при решении задач
Содержание
- 1. Теорема Пифагора и ее применение при решении задач
- 2. Цель урока:Повторить теорему Пифагора;Применять теорему Пифагора при
- 3. Слайд 3
- 4. Без преувеличения можно сказать, что его теорема
- 5. В чем же причина такой популярности Теоремы
- 6. Слайд 6
- 7. Гипотенуза больше катета. Сумма острых углов прямоугольного
- 8. Формулировка Пифагора Площадь квадрата, построенного на гипотенузе
- 9. Устные задачиЗаписать теорему Пифагора для треугольникаАВС
- 10. Устные задачиЗаписать теорему Пифагора для треугольникаАВСЕDМ
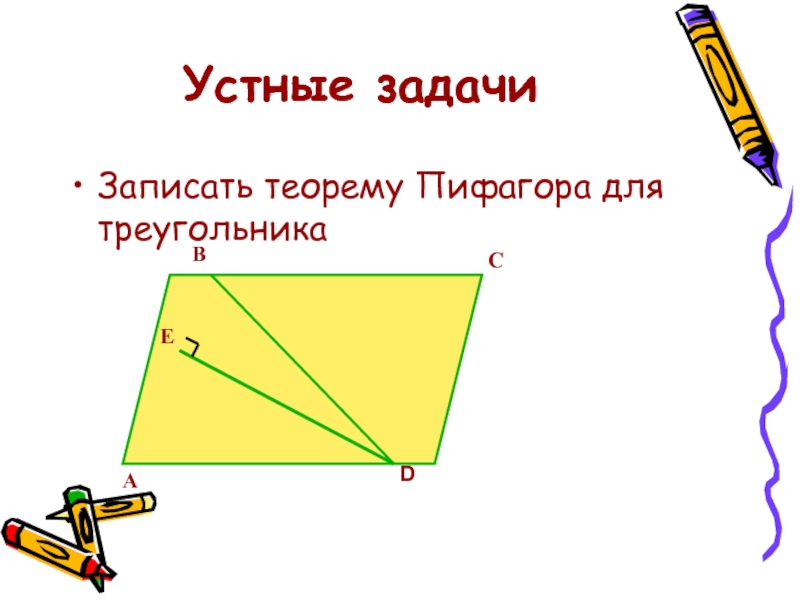
- 11. Устные задачиЗаписать теорему Пифагора для треугольника
- 12. Устные задачиЗаписать теорему Пифагора для треугольника
- 13. Устные задачиЗаписать теорему Пифагора для треугольника
- 14. Алгоритм решения задач с применением теоремы ПифагораУказать
- 15. Найти катет прямоугольного треугольника, лежащий против угла
- 16. На какое расстояние надо отодвинуть от стены
- 17. На какое расстояние надо отодвинуть от стены
- 18. Задача древних индусов Над
- 19. Решение:
- 20. На берегу реки рос тополь одинокий.Вдруг
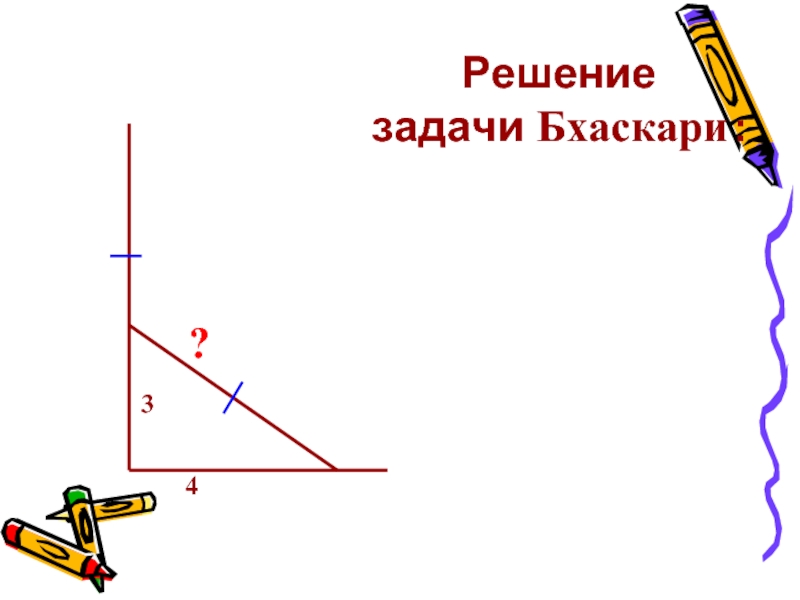
- 21. Решение задачи Бхаскари :34?
- 22. Решив задачи, узнаете, какой стиль архитектуры использовался в Древнем Египте при строительстве!
- 23. ОТВЕТЫ
- 24. Собор Парижской Богоматери
- 25. Домашнее задание:Повторить п.48 - 55«5» - задача №499«4» - задача №498«3» -задача №484 (а, г).
- 26. Итог урока «Сегодня на уроке я повторил…»«Сегодня на уроке я узнал…»«Сегодня на уроке я научился…»
- 27. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли
- 28. Теорема Пифагора Итак,Если дан нам треугольник,И притом
- 29. успешно усвоил теорему Пифагора, выполнил все задания,
- 30. Первый уровень1. Найдите стороны ромба, если его
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Цель урока:
Повторить теорему Пифагора;
Применять теорему Пифагора при решении простейших задач
геометрии;
Рассмотреть исторические задачи;
Рассмотреть решение некоторых задач учебного пособия
Слайд 4Без преувеличения можно сказать, что его теорема самая известная теорема
геометрии, ибо о ней знает подавляющее большинство населения планеты, хотя
доказать ее способна лишь очень незначительная его часть.
Слайд 5В чем же причина такой популярности
Теоремы Пифагора
Знатоки утверждают,
что причин здесь три:
б) красота,
а) простота,
в) значимость
в практическом применении.
Слайд 7
Гипотенуза больше катета.
Сумма острых углов прямоугольного треугольника равна 1800.
Площадь прямоугольного треугольника с катетами а и в вычисляется по
формуле S=ab/2. Теорема Пифагора верна для всех равнобедренных треугольников.
В прямоугольном треугольнике катет, лежащий напротив угла 300, равен половине гипотенузы.
Сумма квадратов катетов равна квадрату гипотенузы.
Квадрат катета равен разности квадратов гипотенузы и второго катета.
Сторона треугольника равна сумме двух других сторон.
Если вы согласны с утверждениями
напротив соответствующего номера вопроса поставьте “+”,
если не согласны, то поставьте “–”.
Слайд 8Формулировка Пифагора
Площадь квадрата, построенного на гипотенузе прямоугольного треуголь-ника, равна
сумме площадей квадратов, построенных на его катетах.
с2 =а2+b2
Современная формулировка
В прямоугольном треу-гольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 14Алгоритм решения задач с применением теоремы Пифагора
Указать прямоугольный треугольник;
Записать для
него теорему Пифагора; с2 = а2+b2
Выразить неизвестную сторону через
две другие;Подставив известные значения, вычислить неизвестную сторону
а
b
с
Слайд 15Найти катет прямоугольного треугольника, лежащий против угла 600, если гипотенуза
равна с
Дано: ▲АВС, <С = 900; <С = 600, АВ = с,
Найти: АС
Решение:
600
С
А
В
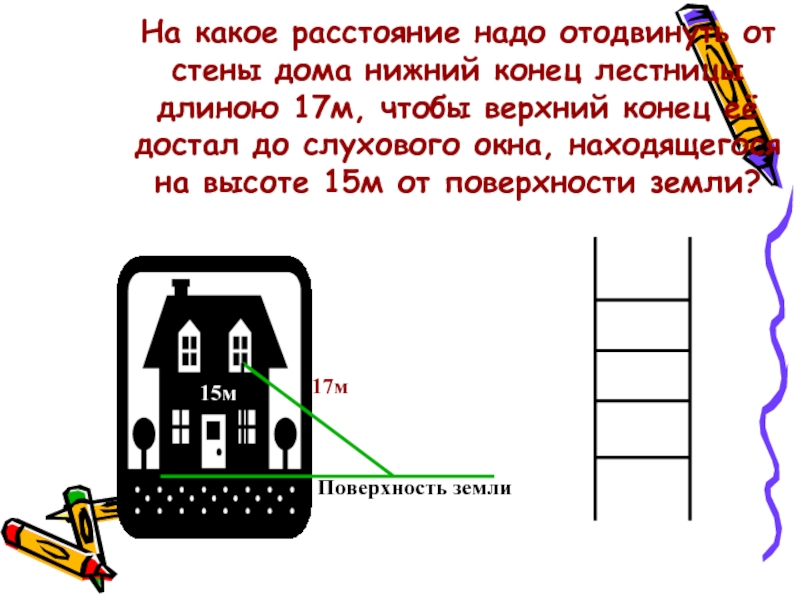
Слайд 16На какое расстояние надо отодвинуть от стены дома нижний конец
лестницы длиною 17м, чтобы верхний конец её достал до слухового
окна, находящегося на высоте 15м от поверхности земли?17м
15м
Поверхность земли
Слайд 17На какое расстояние надо отодвинуть от стены дома нижний конец
лестницы длиною 17м, чтобы верхний конец её достал до слухового
окна, находящегося на высоте 15м от поверхности земли? Дано: ▲АВС
АВ=17м, АС=15м,
Найти: СВ
17м
?
С
В
А
15м
Слайд 18 Задача древних индусов
Над озером тихим,
С полфута
размером, высился лотоса цвет. Он рос одиноко. И ветер порывом Отнес его
в сторону. Нет Боле цветка над водой, Нашел же рыбак его ранней весной В двух футах от места, где рос. Итак, предложу я вопрос: Как озера вода Здесь глубока?Слайд 20 На берегу реки рос тополь одинокий.
Вдруг ветра порыв его
ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его
ствол составлял.Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
Задача индийского
математика XII века
Бхаскари:
Слайд 22Решив задачи, узнаете, какой стиль архитектуры использовался в Древнем Египте при
строительстве!
Слайд 25Домашнее задание:
Повторить п.48 - 55
«5» - задача №499
«4» - задача
№498
«3» -задача №484 (а, г).
Слайд 26Итог урока
«Сегодня на уроке я повторил…»
«Сегодня на уроке я
узнал…»
«Сегодня на уроке я научился…»
Слайд 27Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее так же
“ветряной мельницей”, составляли стихи вроде “Пифагоровы штаны на все стороны
равны”, рисовали карикатуры.
Слайд 28Теорема Пифагора
Итак,
Если дан нам треугольник,
И притом с прямым углом,
То
квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим
- И таким простым путем
К результату мы придем.
Слайд 29успешно усвоил теорему Пифагора, выполнил все задания, стал участником открытого
урока и еще раз убедился в связи математики с другими
науками.Слайд 30Первый уровень
1. Найдите стороны ромба, если его диагонали равны 24
см и 18 см.
2. Найдите периметр прямоугольника, одна сторона
которого равна 9 см, а диагональ – 15 см.3. Стороны прямоугольника 8 см и 15 см. Найдите его диагонали.
Второй уровень
В равнобокой трапеции основания равны 8 см и 14 см, боковая сторона – 5 см.
Найдите высоту трапеции.
2. Высота равнобедренного треугольника равна 20 см, а его основание – 30 см.
Найдите боковую сторону данного треугольника.
3 .Сторона равностороннего треугольника равна 18√3см. Найдите биссектрису этого треугольника.
Третий уровень
Периметр равнобедренного треугольника равен 24 дм, боковая сторона меньше основания на 1.5 дм.
Найдите высоту этого треугольника.
2. В окружность, радиус которой равен 17 см, вписан прямоугольник.
Найдите стороны этого прямоугольника, если отношение их равно 15:8.
3. На сторонах прямоугольного треугольника АВС построены квадраты, причём S3+S2=1252 см2,
а S1= 100 см2.
Найдите периметр треугольника АВС.