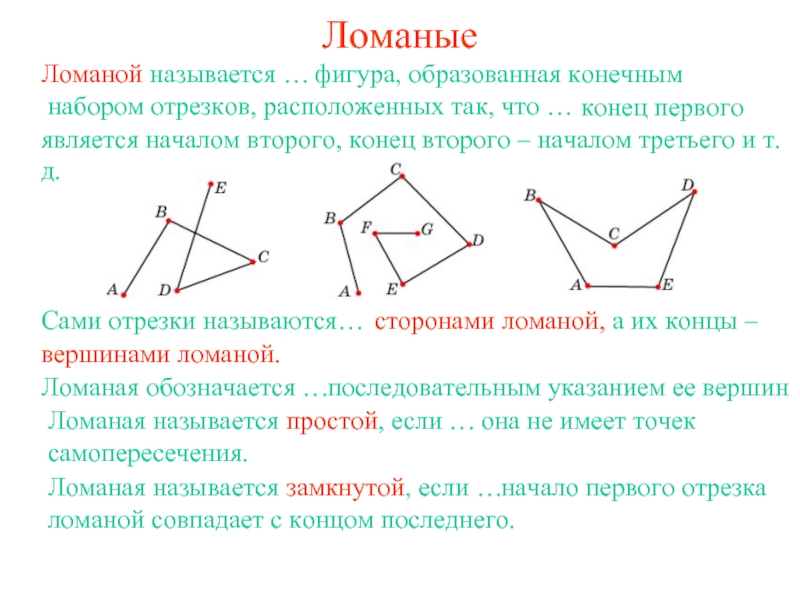
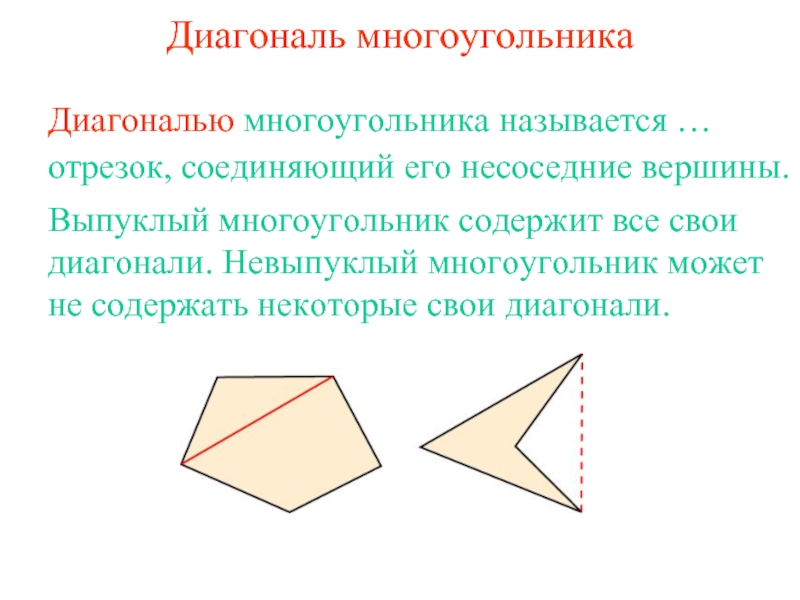
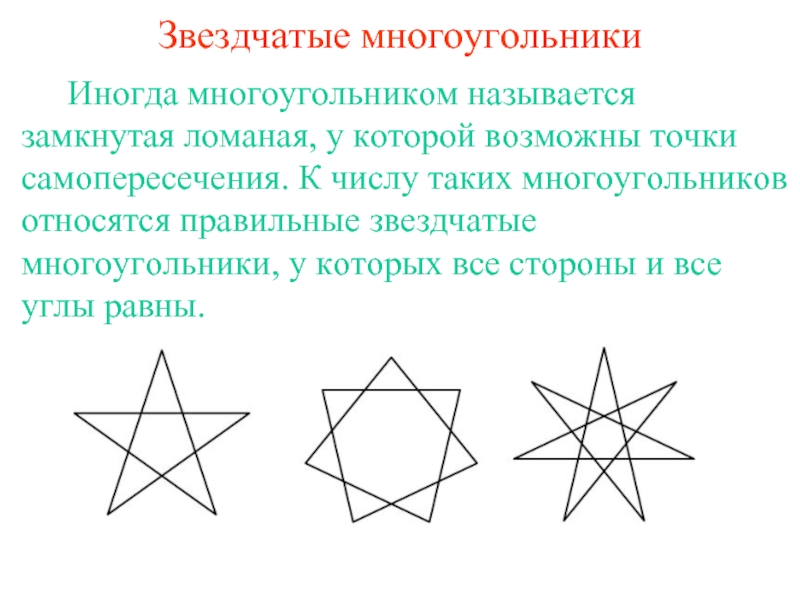
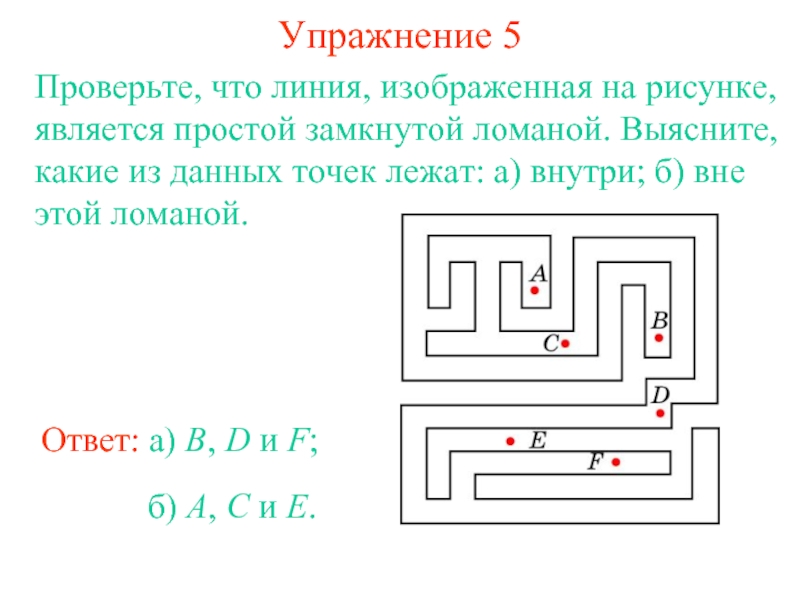
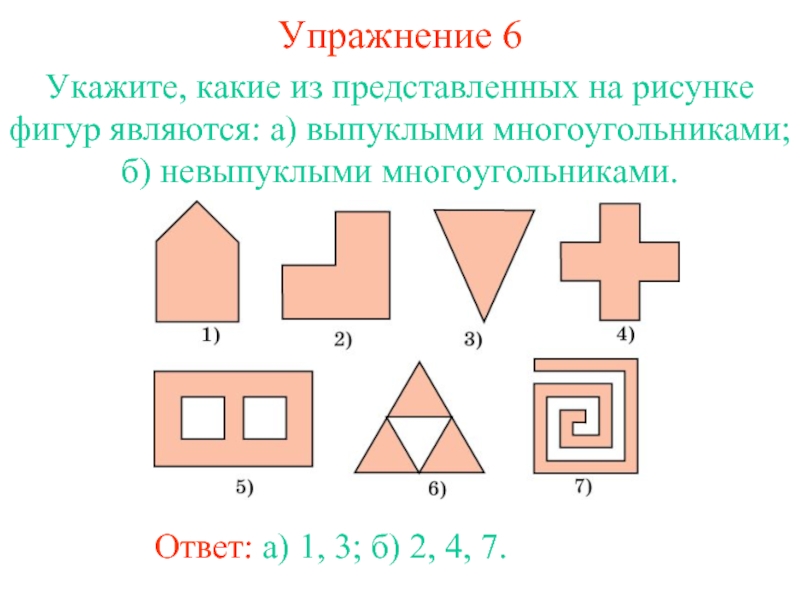
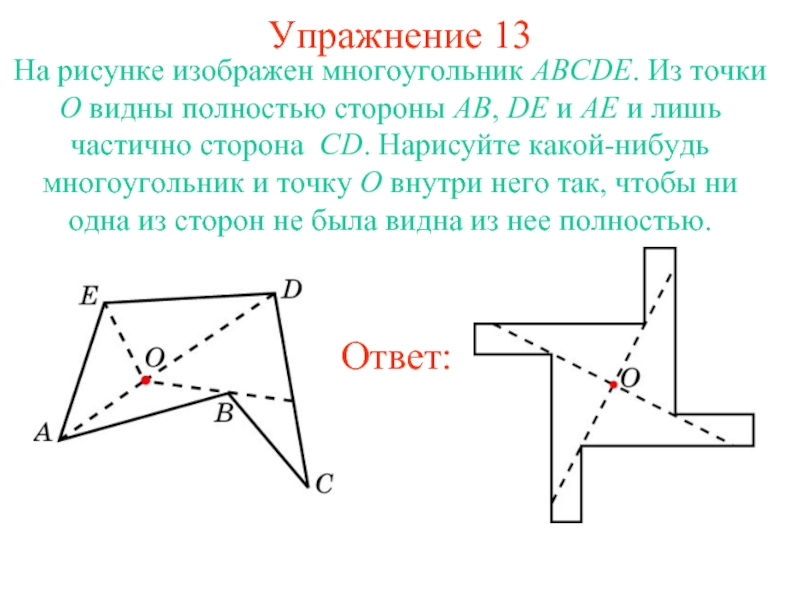
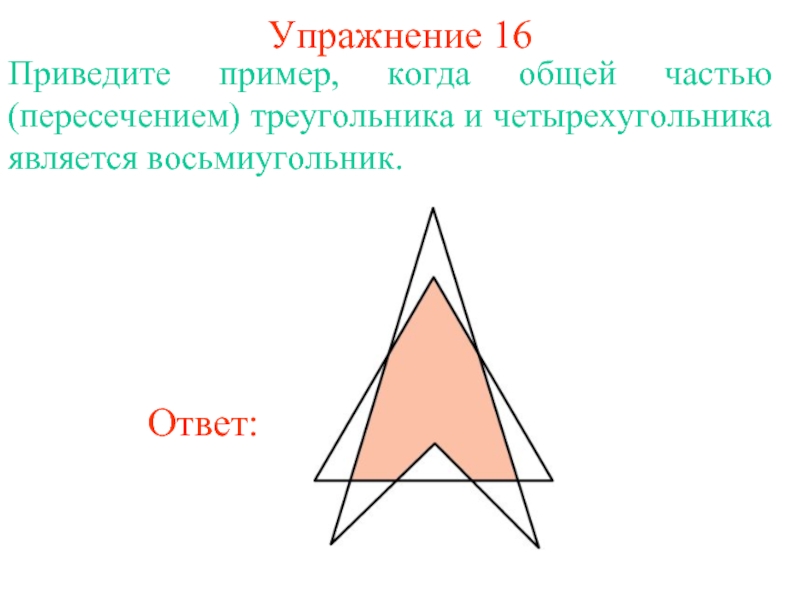
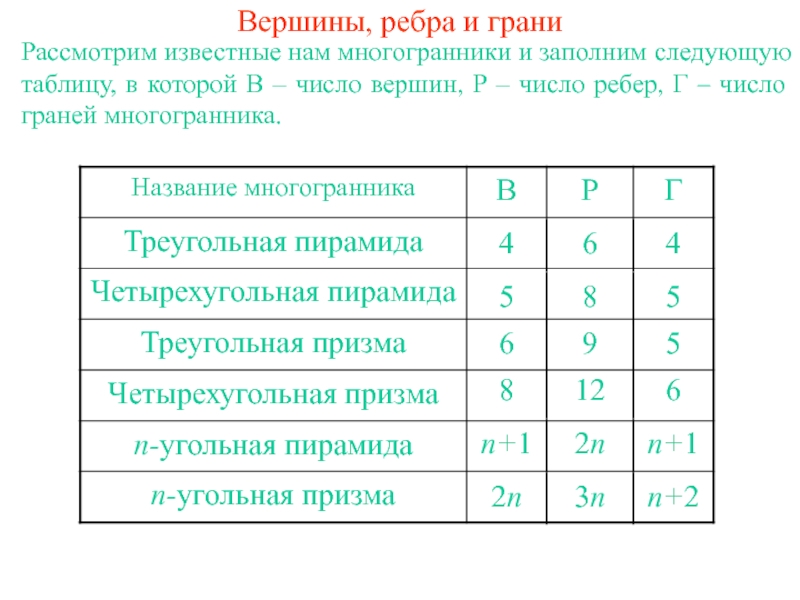
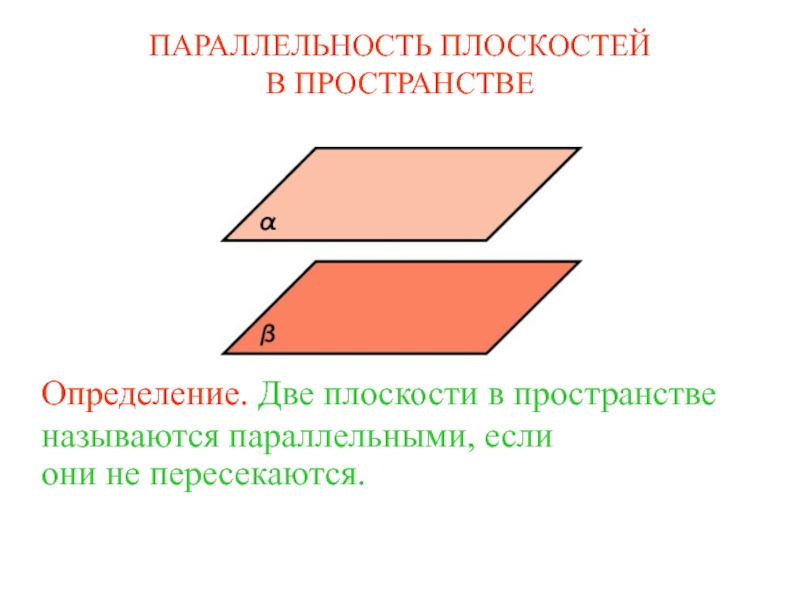
фигура, образованная конечным набором отрезков, расположенных так, что …
Сами отрезки называются…
сторонами ломаной, а их концы –
конец первого является началом второго, конец второго – началом третьего и т.д.
вершинами ломаной.
Ломаная обозначается …
последовательным указанием ее вершин
Ломаная называется простой, если …
она не имеет точек самопересечения.
Ломаная называется замкнутой, если …
начало первого отрезка ломаной совпадает с концом последнего.