Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
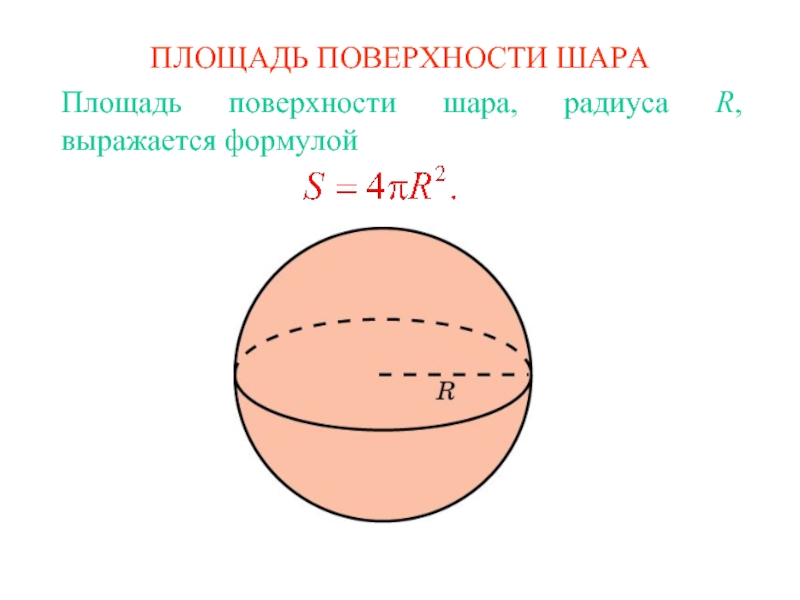
Площадь поверхности шара
Содержание
- 1. Площадь поверхности шара
- 2. ПЛОЩАДЬ ПОВЕРХНОСТИ ШАРОВОГО СЕГМЕНТАПлощадь боковой поверхности шарового сегмента, радиуса R и высотой h, выражается формулой
- 3. ПЛОЩАДЬ ПОВЕРХНОСТИ ШАРОВОГО ПОЯСАПлощадь боковой поверхности шарового пояса, радиуса R и высотой h, выражается формулой
- 4. Упражнение 1Площадь большого круга шара равна 3 см2. Найдите площадь поверхности шара.Ответ: 12 см2.
- 5. Упражнение 2Как изменится площадь поверхности шара, если
- 6. Упражнение 3Площади поверхностей двух шаров относятся как 4 : 9. Найдите отношение их диаметров.Ответ: 2:3.
- 7. Упражнение 4Объём шара равен 288 дм3. Найдите площадь его поверхности.Ответ: 144 дм2.
- 8. Упражнение 5Сечение шара плоскостью, отстоящей от центра
- 9. Упражнение 6Около шара описан цилиндр. Найдите отношение их площадей поверхностей и объемов. Ответ: 2:3; 2:3.
- 10. Упражнение 7Сечение шара плоскостью, отстоящей от центра
- 11. Упражнение 8Во сколько раз площадь поверхности шара,
- 12. Упражнение 9Около прямоугольного параллелепипеда, измерения которого равны
- 13. Упражнение 10Около октаэдра, ребро которого равно 2
- 14. Упражнение 11Около шара описан цилиндр. Найдите отношение
- 15. Упражнение 12Найдите площадь поверхности шарового сегмента, отсекаемого
- 16. Упражнение 13Шар радиуса 1 пересечен двумя параллельными
- 17. ПЛОЩАДЬ СФЕРИЧЕСКОГО МНОГОУГОЛЬНИКАСферическим многоугольником будем называть часть
- 18. Упражнение 14В сферу радиуса 1 вписан правильный
- 19. Упражнение 15Найдите площадь сферического треугольника на единичной
- 20. Упражнение 16Найдите площадь сферического треугольника на единичной
- 21. Упражнение 17Центром единичной сферы является вершина правильной
- 22. Упражнение 18Найдите площадь сферического треугольника, образованного трехгранным
- 23. Упражнение 19Найдите площадь сферического четырехугольника, образованного четырехгранным
- 24. Упражнение 20Найдите площадь сферического пятиугольника, образованного пятигранным
- 25. Упражнение 21Найдите площадь сферического треугольника, образованного трехгранным
- 26. Скачать презентанцию
ПЛОЩАДЬ ПОВЕРХНОСТИ ШАРОВОГО СЕГМЕНТАПлощадь боковой поверхности шарового сегмента, радиуса R и высотой h, выражается формулой
Слайды и текст этой презентации
Слайд 2ПЛОЩАДЬ ПОВЕРХНОСТИ ШАРОВОГО СЕГМЕНТА
Площадь боковой поверхности шарового сегмента, радиуса R
и высотой h, выражается формулой
Слайд 3ПЛОЩАДЬ ПОВЕРХНОСТИ ШАРОВОГО ПОЯСА
Площадь боковой поверхности шарового пояса, радиуса R
и высотой h, выражается формулой
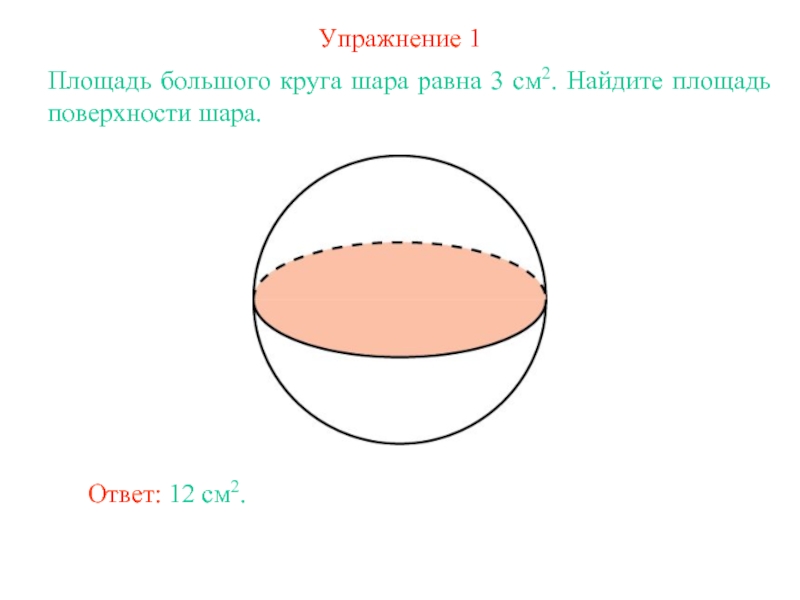
Слайд 4Упражнение 1
Площадь большого круга шара равна 3 см2. Найдите площадь
поверхности шара.
Ответ: 12 см2.
Слайд 5Упражнение 2
Как изменится площадь поверхности шара, если увеличить радиус шара
в: а) 2 раза; б) 3 раза; в) n раз?
Ответ:
Увеличится в: а) 4 раза; б) 9 раз; в) n2 раз. Слайд 6Упражнение 3
Площади поверхностей двух шаров относятся как 4 : 9.
Найдите отношение их диаметров.
Ответ: 2:3.
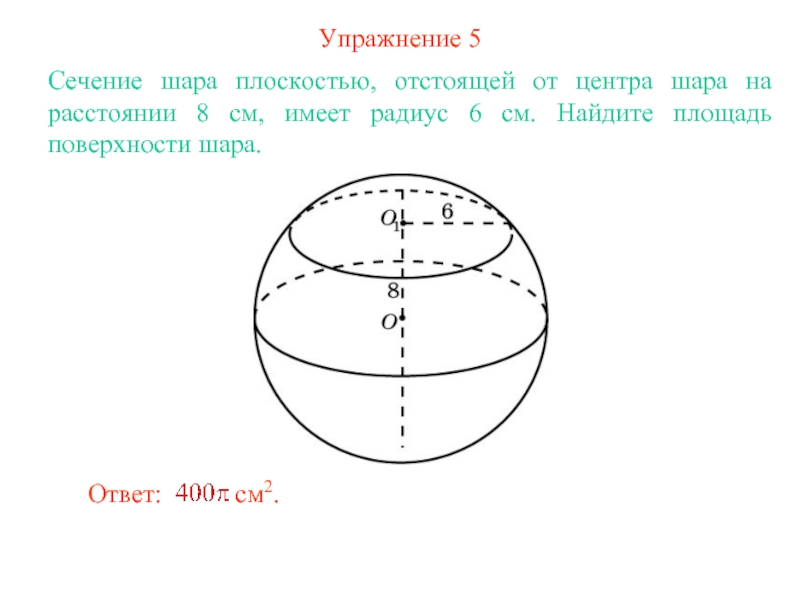
Слайд 8Упражнение 5
Сечение шара плоскостью, отстоящей от центра шара на расстоянии
8 см, имеет радиус 6 см. Найдите площадь поверхности шара.
Слайд 9Упражнение 6
Около шара описан цилиндр. Найдите отношение их площадей поверхностей
и объемов.
Ответ: 2:3; 2:3.
Слайд 10Упражнение 7
Сечение шара плоскостью, отстоящей от центра шара на расстоянии
8 см, имеет радиус 6 см. Найдите площадь поверхности шара.
Слайд 11Упражнение 8
Во сколько раз площадь поверхности шара, описанного около куба,
больше площади поверхности шара, вписанного в этот же куб?
Ответ: В
три раза. Слайд 12Упражнение 9
Около прямоугольного параллелепипеда, измерения которого равны 1 дм, 2
дм и 3 дм, описан шар. Найдите площадь его поверхности.
Ответ:
14 дм2.Слайд 13Упражнение 10
Около октаэдра, ребро которого равно 2 дм, описан шар.
Найдите площадь поверхности шара.
Ответ: 8π дм2.
Слайд 14Упражнение 11
Около шара описан цилиндр. Найдите отношение их площадей поверхностей
и объемов.
Ответ: 2 : 3, 2 : 3.
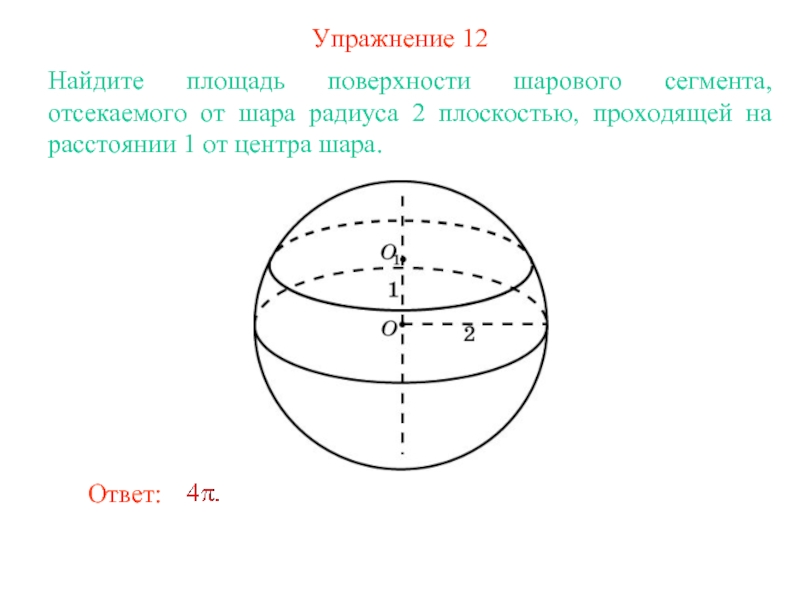
Слайд 15Упражнение 12
Найдите площадь поверхности шарового сегмента, отсекаемого от шара радиуса
2 плоскостью, проходящей на расстоянии 1 от центра шара.
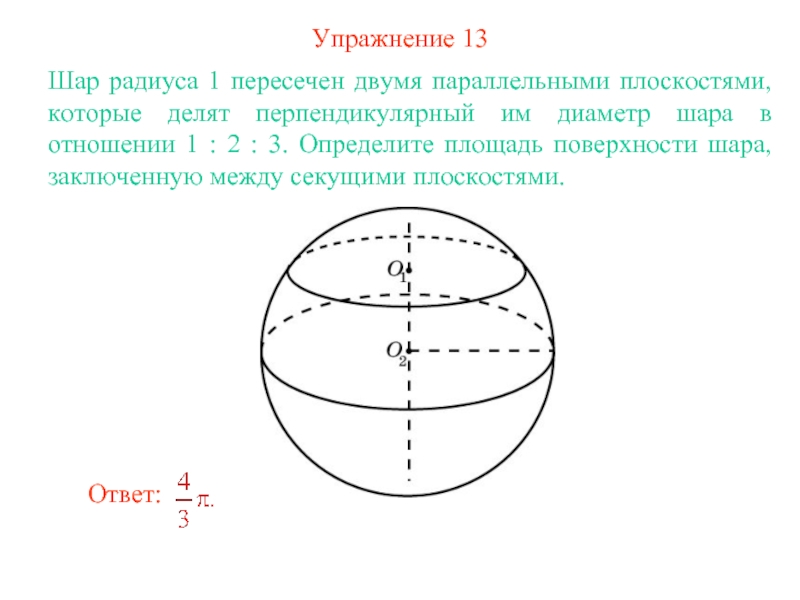
Слайд 16Упражнение 13
Шар радиуса 1 пересечен двумя параллельными плоскостями, которые делят
перпендикулярный им диаметр шара в отношении 1 : 2 :
3. Определите площадь поверхности шара, заключенную между секущими плоскостями.Слайд 17ПЛОЩАДЬ СФЕРИЧЕСКОГО МНОГОУГОЛЬНИКА
Сферическим многоугольником будем называть часть сферы, заключенной внутри
многогранного угла с вершиной в центре сферы.
Напомним, что численная величина
многогранного угла равна половине площади сферического многоугольника, высекаемого многогранным углом из единичной сферы с центром в вершине данного многогранного угла (см. раздел «Многогранные углы»). где A1, …, An – углы сферического многоугольника, равные соответствующим двугранным углам многогранного угла OA1…An
Площадь сферического n-угольника A1…An на сфере с центром O и радиусом R выражается формулой
Слайд 18Упражнение 14
В сферу радиуса 1 вписан правильный тетраэдр, и три
его грани, исходящие из одной вершины, продолжены до пересечения со
сферой. Вычислите площадь части поверхности сферы, заключенной внутри образовавшегося трехгранного угла.Слайд 19Упражнение 15
Найдите площадь сферического треугольника на единичной сфере, углы которого
равны: а) 90о; б) 90о; в) 90о.
Решение. Данный треугольник
составляет одну восьмую часть единичной сферы. Слайд 20Упражнение 16
Найдите площадь сферического треугольника на единичной сфере, углы которого
равны: а) 80о; б) 90о; в) 100о.
Слайд 21Упражнение 17
Центром единичной сферы является вершина правильной четырехугольной пирамиды с
ребром основания 2 и высотой 1. Найдите площадь части сферы,
заключенной внутри пирамиды.Слайд 22Упражнение 18
Найдите площадь сферического треугольника, образованного трехгранным углом единичного тетраэдра
ABCD и единичной сферой с центром в вершине D тетраэдра.
Слайд 23Упражнение 19
Найдите площадь сферического четырехугольника, образованного четырехгранным углом единичного октаэдра
SABCDS’ и единичной сферой с центром в вершине S октаэдра.
Слайд 24Упражнение 20
Найдите площадь сферического пятиугольника, образованного пятигранным углом единичного икосаэдра
и единичной сферой с центром в вершине икосаэдра.
Слайд 25Упражнение 21
Найдите площадь сферического треугольника, образованного трехгранным углом единичного додекаэдра
и единичной сферой с центром в вершине додекаэдра.
Теги