Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Удивительный квадрат (10 класс)
Содержание
- 1. Удивительный квадрат (10 класс)
- 2. целью работы показать практические возможности применения квадрата как геометрической фигуры.
- 3. Задачи: углубить имеющие знания и приобрести новые;познакомить
- 4. Что такое квадрат? Квадратом называется прямоугольник, у которого все стороны равны.
- 5. Замечательные свойства квадрата:Все углы квадрата прямые.Все стороны
- 6. Чем квадрат "лучше" других четырёхугольников?Площадь квадрата больше площади любого прямоугольника с тем же периметром.
- 7. Магический квадрат третьего порядка Здесь изображен единственный
- 8. Магический квадрат Дюрера Четыре средних числа тоже дают
- 9. Как Абул Вефа составил квадрат из трёх
- 10. Задача на разрезание квадрата #1(Результат) Но теперь надо
- 11. Игра с квадратом «Край в край» Сколько фигур
- 12. Упакованные квадраты (Задача) Поскольку гармонический ряд расходится,
- 13. Упакованные квадраты (Результат)Рис. 61/71/81/21/3111/21/41/81/41/51/81/7
- 14. Танграмы Эта головоломка изобретена в Древнем Китае (у
- 15. Танграмы (Изображения 1)
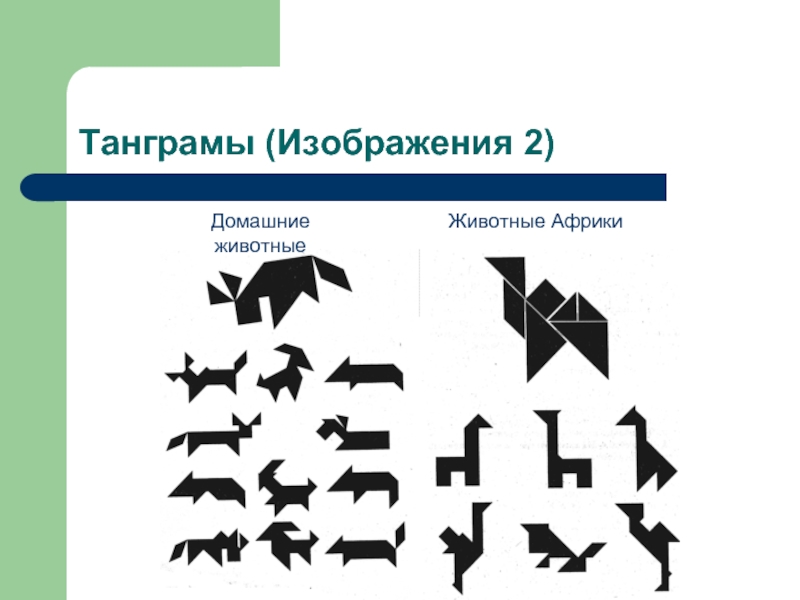
- 16. Танграмы (Изображения 2)Домашние животныеЖивотные Африки
- 17. Построение при помощи перегибания квадратного листа бумаги 1-й способ2-ой способПервый сгибВторой сгибЧетвертый сгибТретий сгиб
- 18. Построение при помощи перегибания квадратного листа бумагиПервый сгибВторой сгибТретий сгибЧетвертый сгиб3-й способ
- 19. Скачать презентанцию
целью работы показать практические возможности применения квадрата как геометрической фигуры.
Слайды и текст этой презентации
Слайд 1«Удивительный квадрат»
Исполнитель:
Новоселов Андрей
Ученик 10 класса «Г»
МОУ СОШ № 10
Руководитель:
Овсянникова
И. В.
Слайд 2 целью работы
показать практические возможности применения квадрата как
геометрической фигуры.
Слайд 3Задачи:
углубить имеющие знания и приобрести новые;
познакомить с особенностями периметра и
площади квадрата в сравнении с прямоугольником;
расширить знания по решению задач
с практическим содержанием.
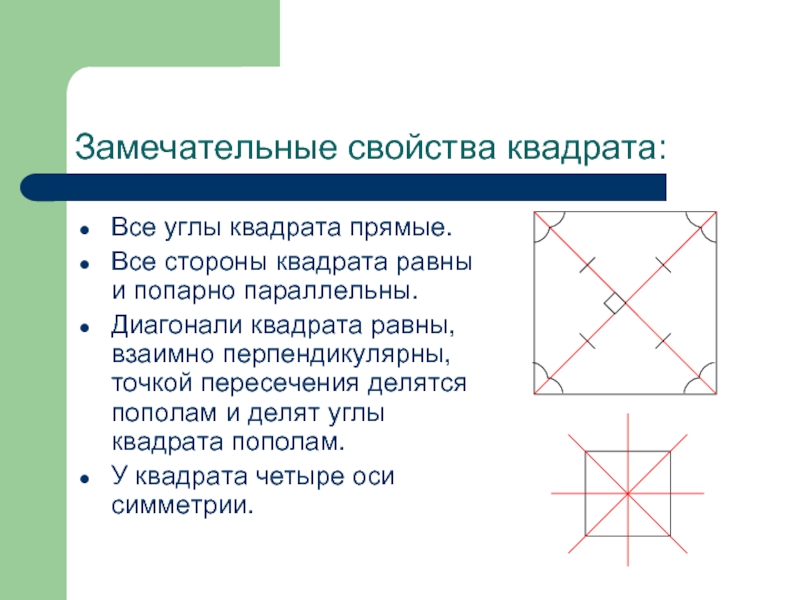
Слайд 5Замечательные свойства квадрата:
Все углы квадрата прямые.
Все стороны квадрата равны и
попарно параллельны.
Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам
и делят углы квадрата пополам.У квадрата четыре оси симметрии.
Слайд 6Чем квадрат "лучше" других четырёхугольников?
Площадь квадрата больше площади любого прямоугольника
с тем же периметром.
Слайд 7Магический квадрат третьего порядка
Здесь изображен единственный магический квадрат третьего
порядка. Если ты найдешь семь других возможных расположений чисел, ты
увидишь, что все они получаются из этого или отражениями, или поворотами.15
15
15
15
15
15
15
15
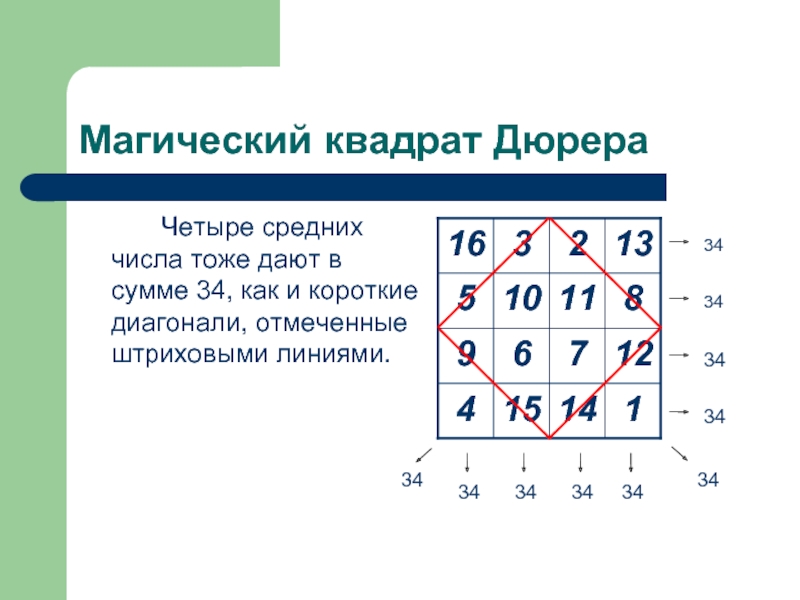
Слайд 8Магический квадрат Дюрера
Четыре средних числа тоже дают в сумме 34,
как и короткие диагонали, отмеченные штриховыми линиями.
34
34
34
34
34
34
34
34
34
34
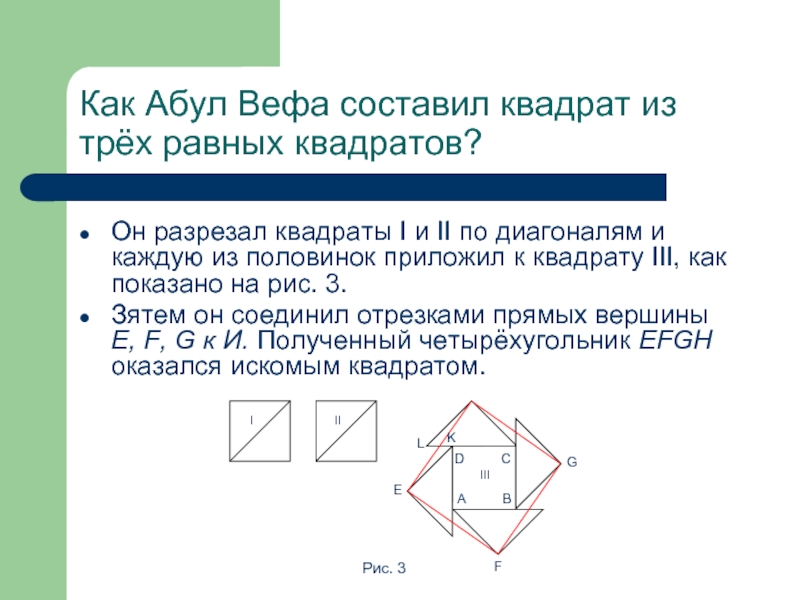
Слайд 9Как Абул Вефа составил квадрат из трёх равных квадратов?
Он разрезал
квадраты I и II по диагоналям и каждую из половинок
приложил к квадрату III, как показано на рис. 3.Зятем он соединил отрезками прямых вершины E, F, G к И. Полученный четырёхугольник EFGH оказался искомым квадратом.
Слайд 10Задача на разрезание квадрата #1(Результат)
Но теперь надо еще показать, что
шесть разрезов можно в действительности осуществить так, чтобы каждый раз
число частей удваивалось и в результате получилось 26 = 64 отдельных квадратика. Это уже не трудно сделать: надо только следить, чтобы после каждого разреза все части оказывались равными, и чтобы каждый очередной разрез разбивал каждую из частей пополам.После первого разреза
После второго разреза
После третьего разреза
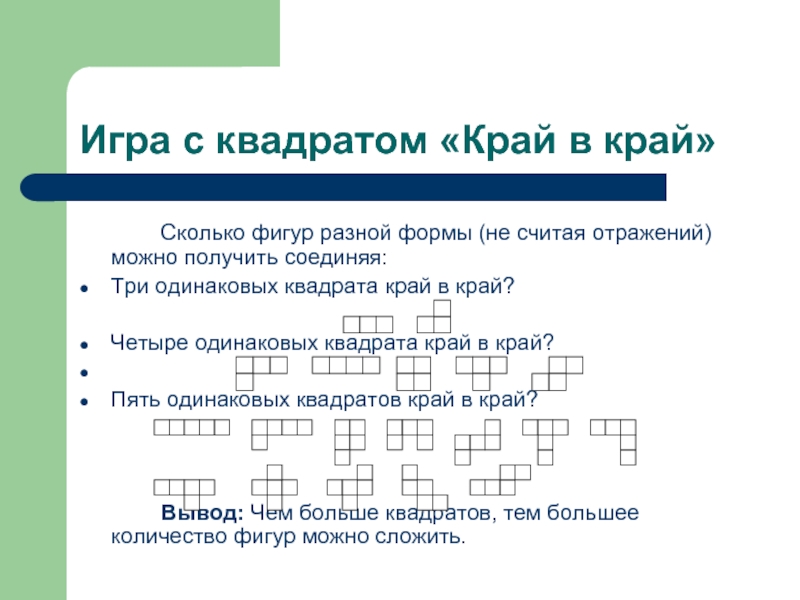
Слайд 11Игра с квадратом «Край в край»
Сколько фигур разной формы (не
считая отражений) можно получить соединяя:
Три одинаковых квадрата край в край?
Четыре одинаковых квадрата край в край?
Пять одинаковых квадратов край в край?
Вывод: Чем больше квадратов, тем большее количество фигур можно сложить.
Слайд 12Упакованные квадраты (Задача)
Поскольку гармонический ряд расходится, множество квадратов со
сторонами 1, 1/2, 1/3, … , 1/ n, … ,
приставленных друг к другу на прямой L (Рис. 5)будет простираться бесконечно далеко по этой прямой. Доказать, что, можно все квадраты, начиная со второго, уложить в первый квадрат без наложений.Слайд 14Танграмы
Эта головоломка изобретена в Древнем Китае (у нас она сейчас
распространена под названием «Пифагор».). Из семи частей квадрата удается сложить
самые разнообразные фигуры.Разрезав квадрат так, как показано на рисунке и соблюдая два правила:
1) при складывании фигурок использовать все семь частей-танов;
2) таны нельзя накладывать друг на друга (они могут только касаться друг друга)
Слайд 17Построение при помощи перегибания квадратного листа бумаги
1-й способ
2-ой способ
Первый
сгиб
Второй сгиб
Четвертый сгиб
Третий сгиб
Слайд 18Построение при помощи перегибания квадратного листа бумаги
Первый сгиб
Второй сгиб
Третий сгиб
Четвертый
сгиб
3-й способ
Теги