Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Медиана, биссектриса и высота треугольника
Содержание
- 1. Медиана, биссектриса и высота треугольника
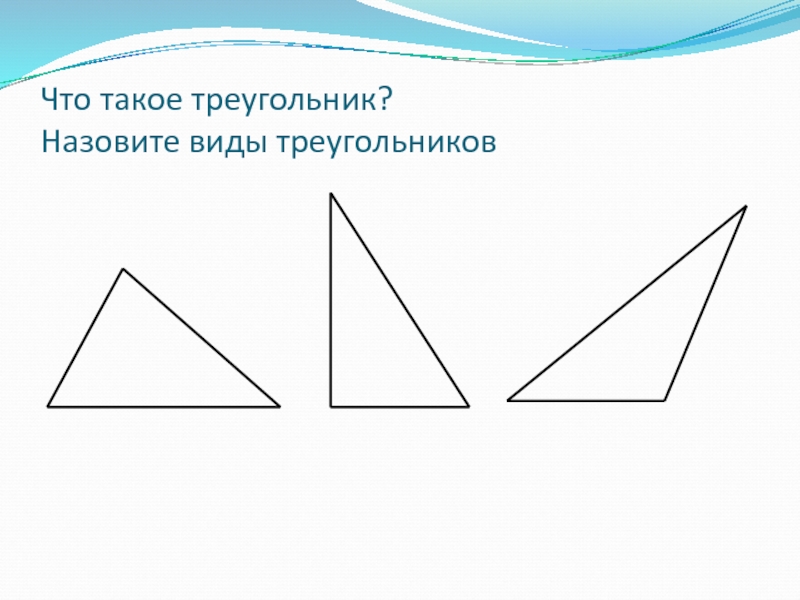
- 2. Что такое треугольник? Назовите виды треугольников
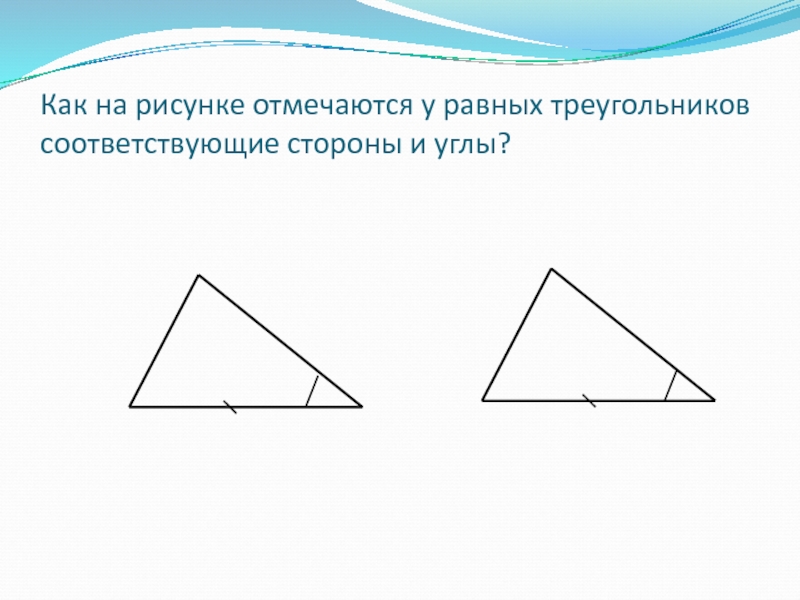
- 3. Как на рисунке отмечаются у равных треугольников соответствующие стороны и углы?
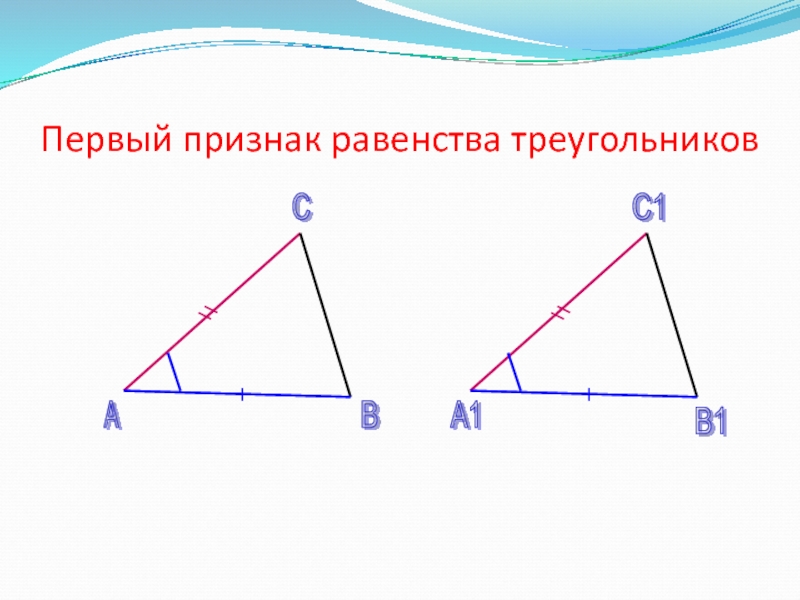
- 4. Первый признак равенства треугольниковА В С А1 В1 С1
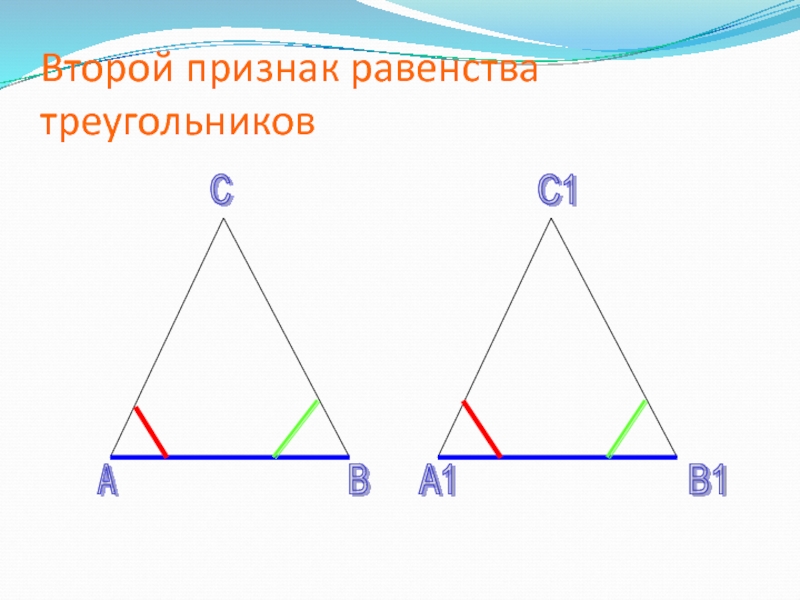
- 5. Второй признак равенства треугольников А В С А1 В1 С1
- 6. Медиана Медианой треугольника, проведенной из данной вершины,
- 7. Биссектриса Биссектрисой треугольника, проведенной из данной вершины,
- 8. ВысотаВысотой треугольника, опущенной из данной вершины, называется
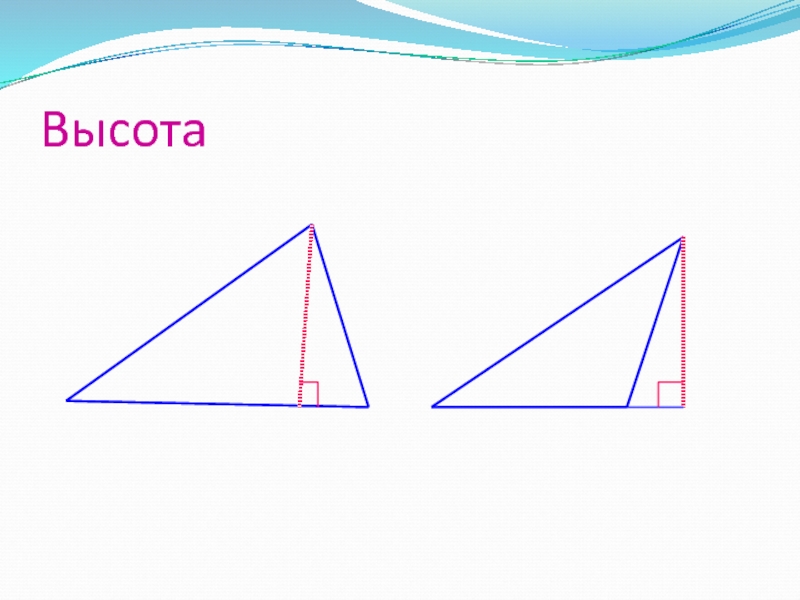
- 9. Высота
- 10. Назовите, чем являются отрезки КС, NL, EF
- 11. Задача В треугольнике АВС проведены биссектриса
- 12. Задание 1 Начертите 3 треугольника –
- 13. Задание 2 Начертите произвольный треугольник. Сколько
- 14. Задача В ΔАВС проведены медианы АD,
- 15. Задача Докажите, что у равных треугольников
- 16. Задача Докажите, что у равных треугольников
- 17. Слайд 17
- 18. Задача Докажите, что у равнобедренного треугольника биссектрисы, проведенные из вершин при основании, равны.
- 19. Задача Докажите, что у равнобедренного треугольника медианы, проведенные из вершин при основании, равны.
- 20. Задача Точки А, В, С,
- 21. Выбери свое настроение
- 22. Оцените свою работу на
- 23. Домашнее заданиеП. 25, в. 8-10, № 23, № 26
- 24. Скачать презентанцию
Что такое треугольник? Назовите виды треугольников
Слайды и текст этой презентации
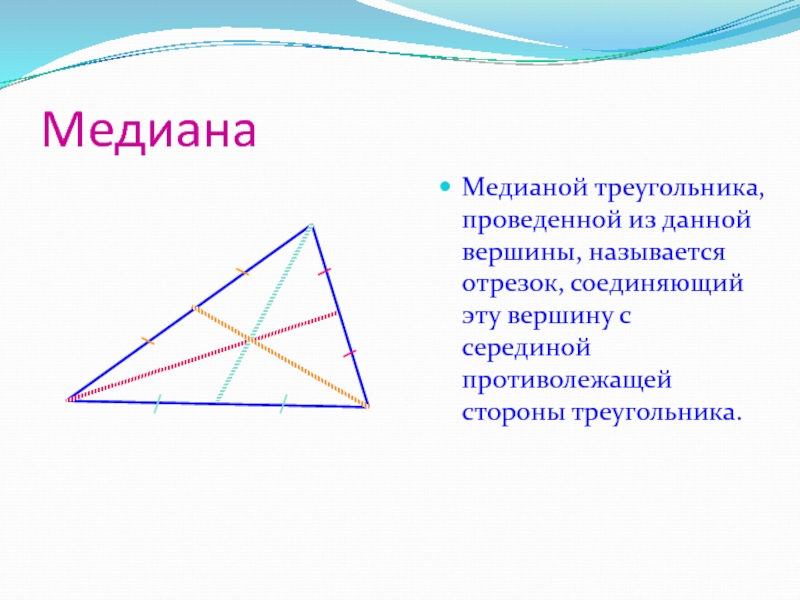
Слайд 6Медиана
Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий
эту вершину с серединой противолежащей стороны треугольника.
Слайд 7Биссектриса
Биссектрисой треугольника, проведенной из данной вершины, называется отрезок угла
треугольника, соединяющий эту вершину с точкой на противолежащей стороне.
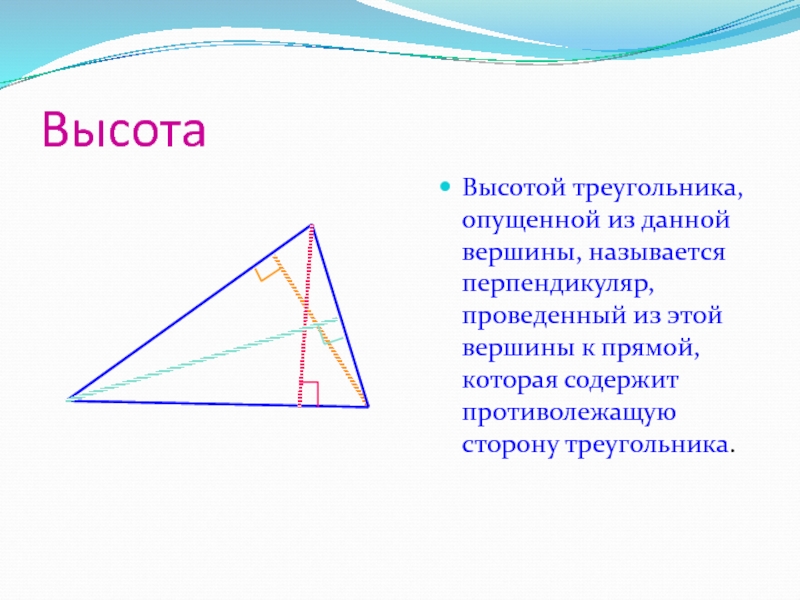
Слайд 8Высота
Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из
этой вершины к прямой, которая содержит противолежащую сторону треугольника.
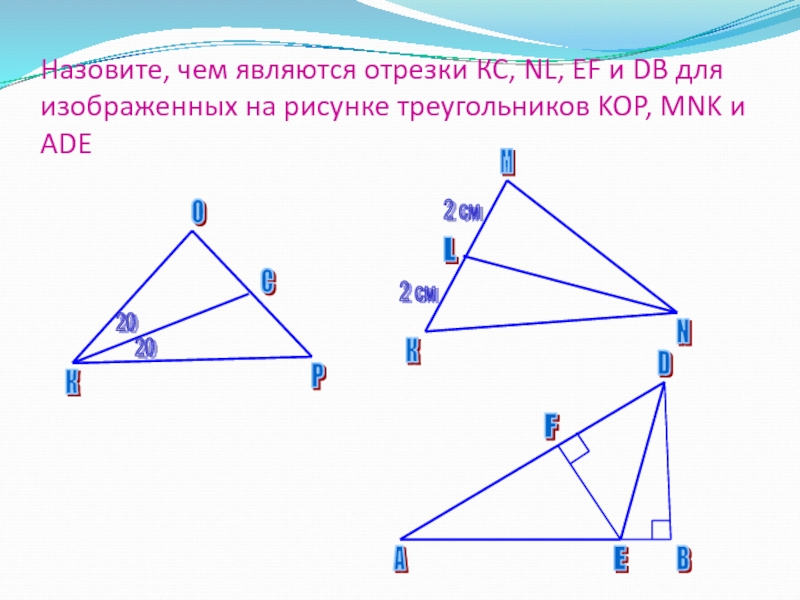
Слайд 10Назовите, чем являются отрезки КС, NL, EF и DB для
изображенных на рисунке треугольников KOP, MNK и ADE
К
О
Р
К
М
N
20
20
L
2 см
2 см
D
F
А
Е
В
С
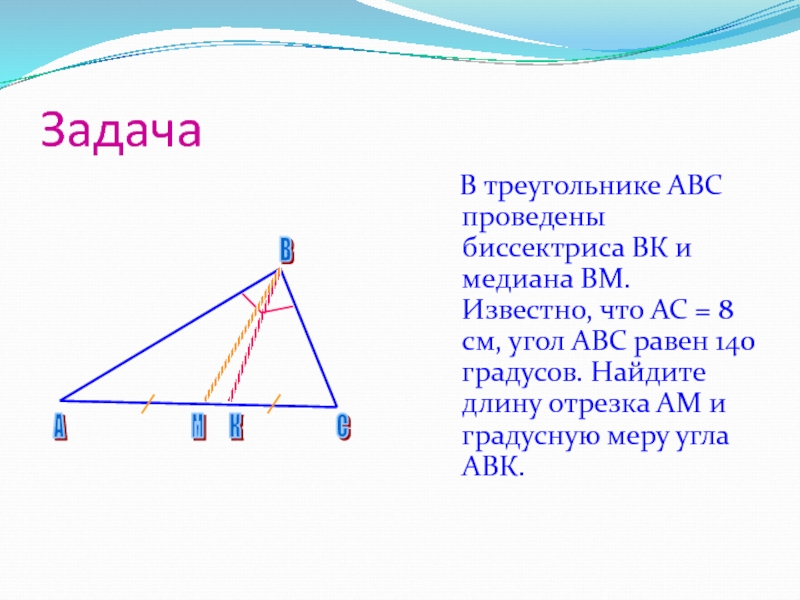
Слайд 11Задача
В треугольнике АВС проведены биссектриса ВК и
медиана ВМ. Известно, что АС = 8 см, угол АВС
равен 140 градусов. Найдите длину отрезка АМ и градусную меру угла АВК.А
В
С
М
К
Слайд 12Задание 1
Начертите 3 треугольника – остроугольный, тупоугольный
и прямоугольный. С помощью угольника проведите в каждом из них
высоту из вершины острого угла.Слайд 13Задание 2
Начертите произвольный треугольник. Сколько медиан можно
в нем провести? Постройте их, используя линейку с делениями.
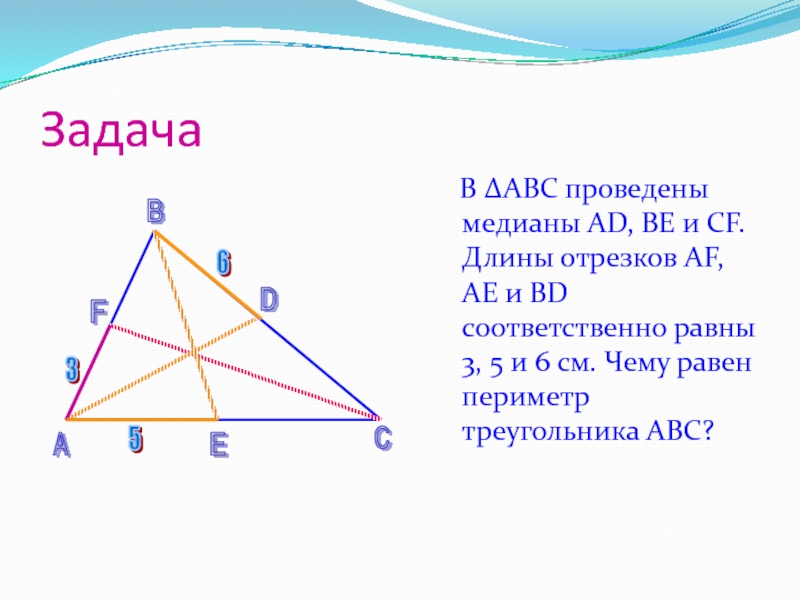
Слайд 14Задача
В ΔАВС проведены медианы АD, ВЕ и
СF. Длины отрезков АF, АЕ и ВD соответственно равны 3,
5 и 6 см. Чему равен периметр треугольника АВС?F
E
D
C
B
A
3
6
5
Слайд 15Задача
Докажите, что у равных треугольников АВС и
А1В1С1 медианы, проведенные из вершин А и А1, равны.
Слайд 16Задача
Докажите, что у равных треугольников АВС и
А1В1С1 биссектрисы, проведенные из вершин А и А1, равны.
Слайд 18Задача
Докажите, что у равнобедренного треугольника биссектрисы, проведенные
из вершин при основании, равны.
Слайд 19Задача
Докажите, что у равнобедренного треугольника медианы, проведенные
из вершин при основании, равны.
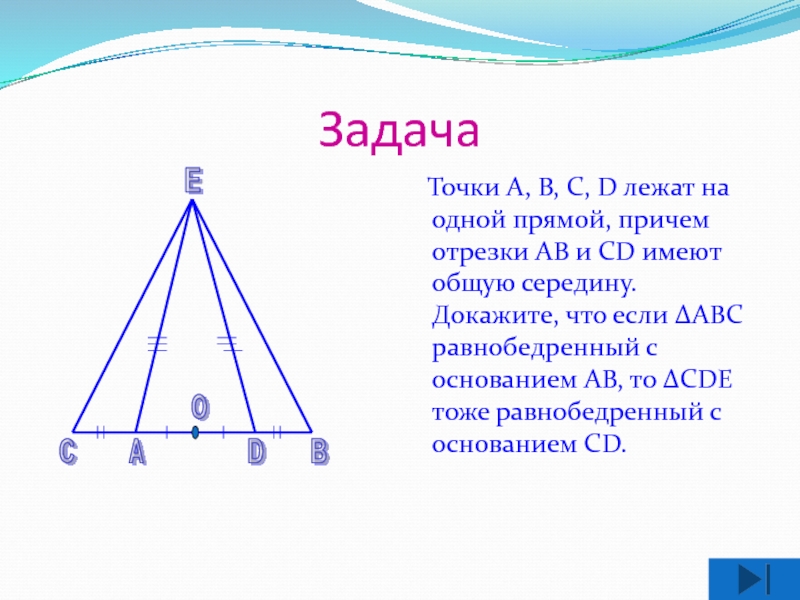
Слайд 20Задача
Точки А, В, С, D лежат
на одной прямой, причем отрезки АВ и СD имеют общую
середину. Докажите, что если ΔАВС равнобедренный с основанием АВ, то ΔСDЕ тоже равнобедренный с основанием СD.Е
D
А
С
В
О