Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аксиомы Точки и прямые
Содержание
- 1. Аксиомы Точки и прямые
- 2. Данная презентация предназначена для проведения обобщающего урока
- 3. Аксиомы Точки и прямыеКакова бы не была
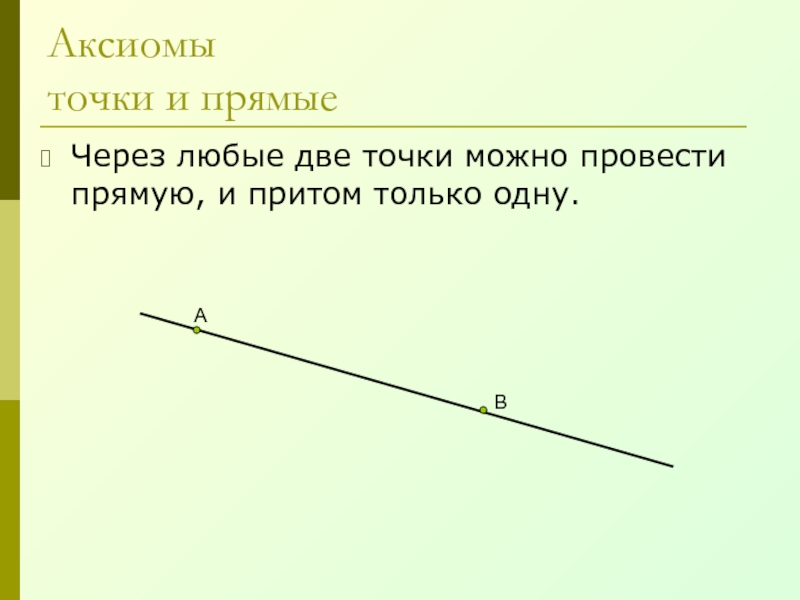
- 4. Аксиомы точки и прямыеЧерез любые две точки можно провести прямую, и притом только одну.АВ
- 5. Аксиомы точки и прямыеИз трёх точек на прямой одна, и только одна, лежит между двумя другими.АВС
- 6. Аксиомы Отрезки и их длиныКаждый отрезок имеет определённую длину.АВАВ = 6 см
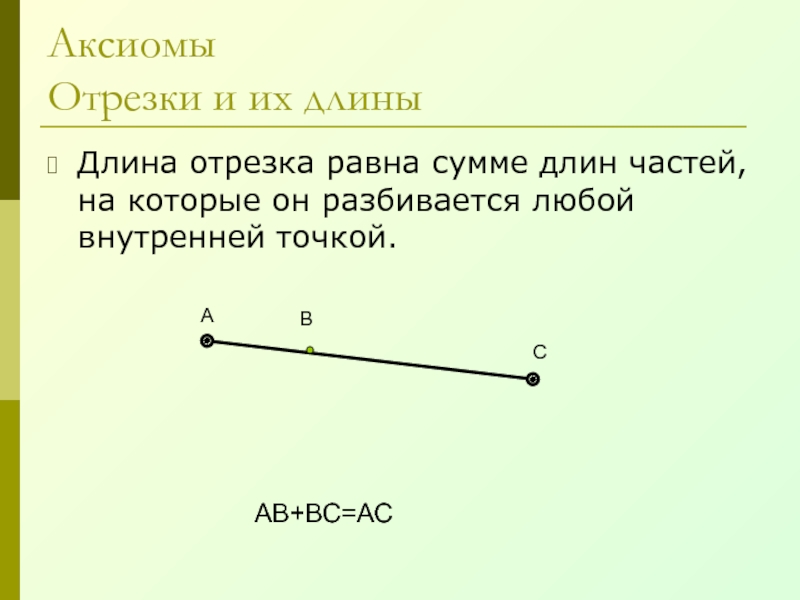
- 7. Аксиомы Отрезки и их длиныДлина отрезка равна
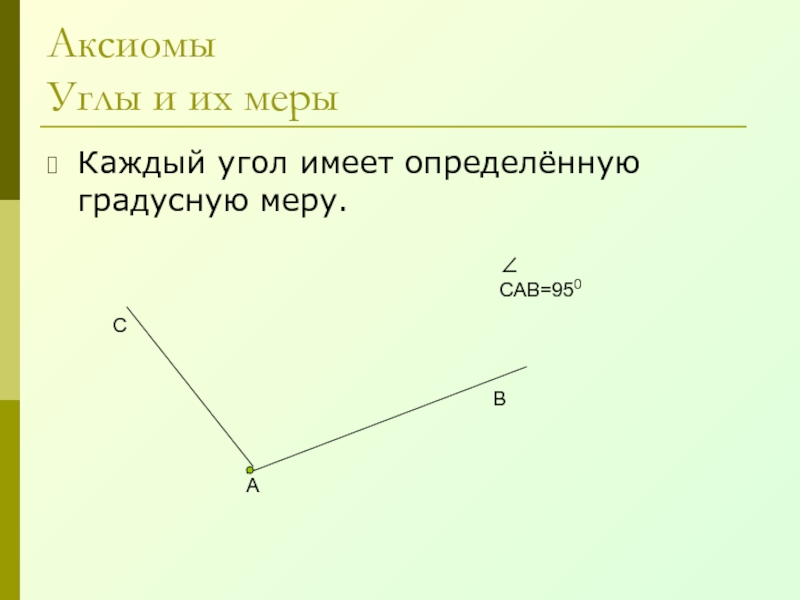
- 8. Аксиомы Углы и их мерыКаждый угол имеет определённую градусную меру.АВС∠ САВ=950
- 9. Аксиомы Углы и их мерыМера угла равна
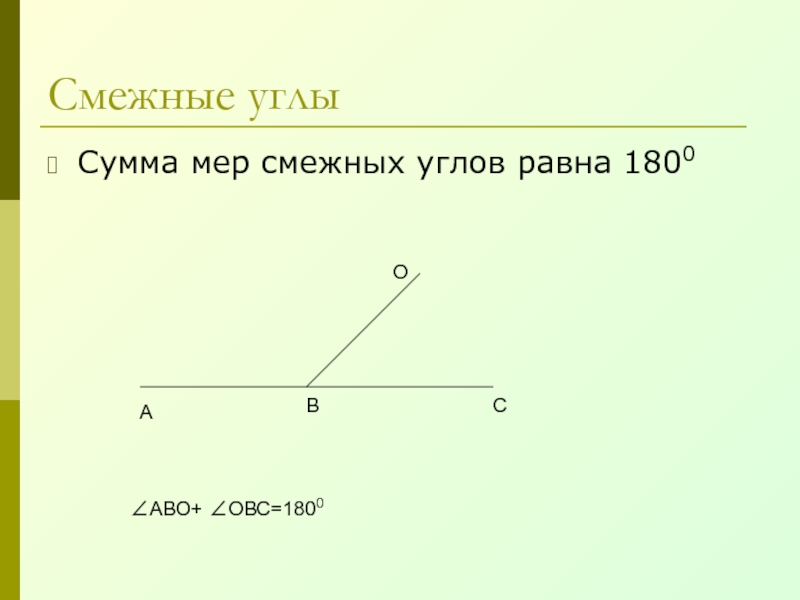
- 10. Смежные углыСумма мер смежных углов равна 1800АВСО∠АВО+ ∠ОВС=1800
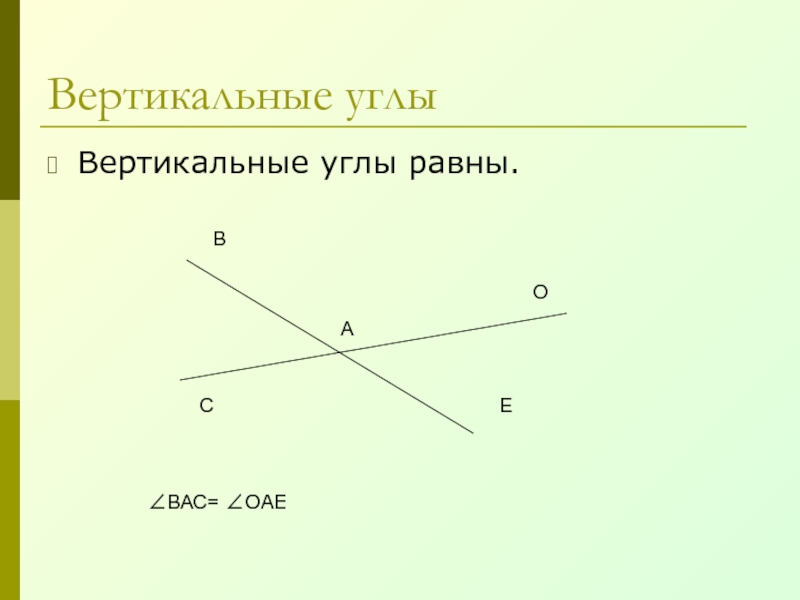
- 11. Вертикальные углыВертикальные углы равны.АВСОЕ∠ВАС= ∠ОАЕ
- 12. Параллельные прямые определениеПрямые называются параллельными, если-они лежат в одной плоскости-они не пересекаютсяава⏐⏐в
- 13. Параллельные прямые ПризнакиЕсли две прямые с поперечиной
- 14. Параллельные прямые ПризнакиЕсли сумма внутренних односторонних углов
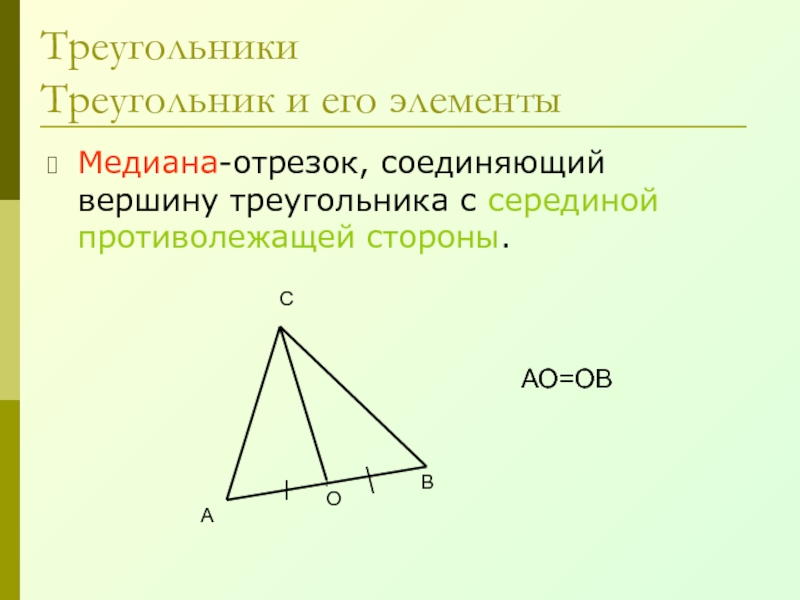
- 15. Треугольники Треугольник и его элементыМедиана-отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.АВСОАО=ОВ
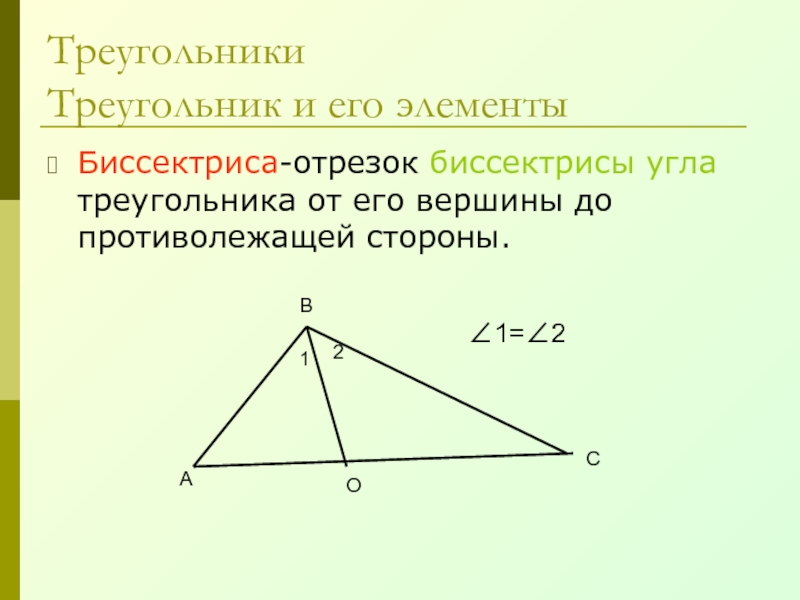
- 16. Биссектриса-отрезок биссектрисы угла треугольника от его вершины до противолежащей стороны.Треугольники Треугольник и его элементыАВСО12∠1=∠2
- 17. Треугольники Треугольник и его элементыВысота- перпендикуляр, опущенный
- 18. Треугольники Треугольник и его элементыСумма углов треугольника равна 1800АВС∠А + ∠В + ∠С = 1800
- 19. Треугольники Треугольник и его элементыУгол, смежный с
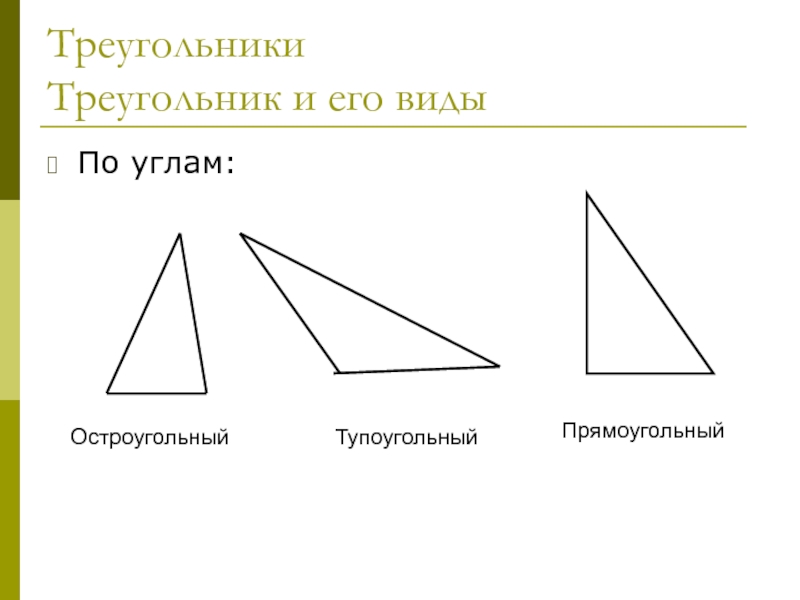
- 20. Треугольники Треугольник и его видыПо углам:ОстроугольныйТупоугольныйПрямоугольный
- 21. Треугольники Треугольник и его виды
- 22. Треугольники Треугольник и его видыПо сторонамразностороннийравнобедренныйравносторонний
- 23. Треугольники Признаки равенстваПервый признакЕсли две стороны и
- 24. Треугольники Признаки равенстваВторой признакЕсли сторона и два
- 25. Треугольники Признаки равенстваТретий признакЕсли три стороны одного
- 26. Равнобедренный треугольник ОпределениеТреугольник называется равнобедренным, если у него две стороны равны.АВСАС, СВ- боковые стороныАС=СВАВ- основание
- 27. Равнобедренный треугольник Свойства В равнобедренном треугольнике углы
- 28. Равнобедренный треугольник ПризнакиЕсли в треугольнике два угла
- 29. Равносторонний треугольник ОпределениеТреугольник называется равносторонним, если у него все стороны равны. АВСАС=АВ=ВС
- 30. Равносторонний треугольник СвойстваВ равностороннем треугольнике все углы
- 31. Равносторонний треугольник ПризнакиЕсли все углы в треугольнике
- 32. Прямоугольный треугольник ОпределениеТреугольник называется прямоугольным, если один из его углов прямой.АВС∠А=900АС, АВ- катетыСВ- гипотенуза
- 33. Прямоугольный треугольник Признаки Если
- 34. Прямоугольный треугольник Признаки Если
- 35. Прямоугольный треугольник Признаки Если
- 36. Прямоугольный треугольник Признаки Если
- 37. Прямоугольный треугольник СвойстваКатет прямоугольного треугольника, лежащий против угла 300, равен половине гипотенузы.АСВ∠А=900∠В=300АС=0,5ВС
- 38. Прямоугольный треугольник СвойстваВ прямоугольном треугольнике сумма острых углов равна 900. АВС∠А=900, ∠В+∠С=900
- 39. Скачать презентанцию
Данная презентация предназначена для проведения обобщающего урока по курсу геометрии 7 класс. Продолжительность показа презентации зависит от степени подготовки класса: от 3 до 4 уроков.Отдельные
Слайды и текст этой презентации
Слайд 2Данная презентация предназначена для проведения обобщающего урока по курсу геометрии
7 класс.
Продолжительность показа
презентации зависит от степени подготовки класса: от 3 до 4 уроков.Отдельные фрагменты презентации можно использовать как при объяснении нового материала, так и при закреплении или повторении.
далее
Слайд 3Аксиомы
Точки и прямые
Какова бы не была прямая, существуют точки, принадлежащие
этой прямой, и точки не принадлежащие ей.
А
В
В
Слайд 5Аксиомы
точки и прямые
Из трёх точек на прямой одна, и только
одна, лежит между двумя другими.
А
В
С
Слайд 7Аксиомы
Отрезки и их длины
Длина отрезка равна сумме длин частей, на
которые он разбивается любой внутренней точкой.
В
А
С
АВ+ВС=АС
Слайд 9Аксиомы
Углы и их меры
Мера угла равна сумме мер углов, на
которые данный угол разбивается любым его внутренним лучом.
А
В
С
О
∠ АВС= ∠АВО
+∠ ОВС
Слайд 12Параллельные прямые
определение
Прямые называются параллельными, если
-они лежат в одной плоскости
-они не
пересекаются
а
в
а⏐⏐в
Слайд 13Параллельные прямые
Признаки
Если две прямые с поперечиной образуют равные накрест лежащие
углы, то прямые параллельны
1
2
3
4
а
в
∠2=∠3⇒ а⏐⏐в
Если две прямые параллельны, то они
с поперечиной образуют равные накрест лежащие углыа⏐⏐в ⇒ ∠2=∠3
Параллельные прямые
Свойства
Слайд 14Параллельные прямые
Признаки
Если сумма внутренних односторонних углов равна 1800 ,то прямые
параллельны
1
2
3
4
а
в
∠2+∠4=1800 ⇒а⏐⏐в
Если сумма внутренних односторонних углов равна 1800 ,то прямые
параллельныЕсли прямые параллельны, то сумма внутренних односторонних углов равна 1800
а⏐⏐в ⇒∠2+∠4=1800
Параллельные прямые
Свойства
Слайд 15Треугольники
Треугольник и его элементы
Медиана-отрезок, соединяющий вершину треугольника с серединой противолежащей
стороны.
А
В
С
О
АО=ОВ
Слайд 16Биссектриса-отрезок биссектрисы угла треугольника от его вершины до противолежащей стороны.
Треугольники
Треугольник
и его элементы
А
В
С
О
1
2
∠1=∠2
Слайд 17Треугольники
Треугольник и его элементы
Высота- перпендикуляр, опущенный из вершины треугольника на
прямую, содержащую противолежащую сторону
А
В
С
О
ВО⊥АС ⇒ ∠ВОС=900
Слайд 18Треугольники
Треугольник и его элементы
Сумма углов треугольника равна 1800
А
В
С
∠А + ∠В
+ ∠С = 1800
Слайд 19Треугольники
Треугольник и его элементы
Угол, смежный с углом треугольника, называют внешним
углом.
.
А
В
С
О
1
∠ВСО=∠1-внешний
∠1=∠А+∠В
Внешний угол треугольника равен
сумме двух внутренних , не смежных
с ним
Слайд 23Треугольники
Признаки равенства
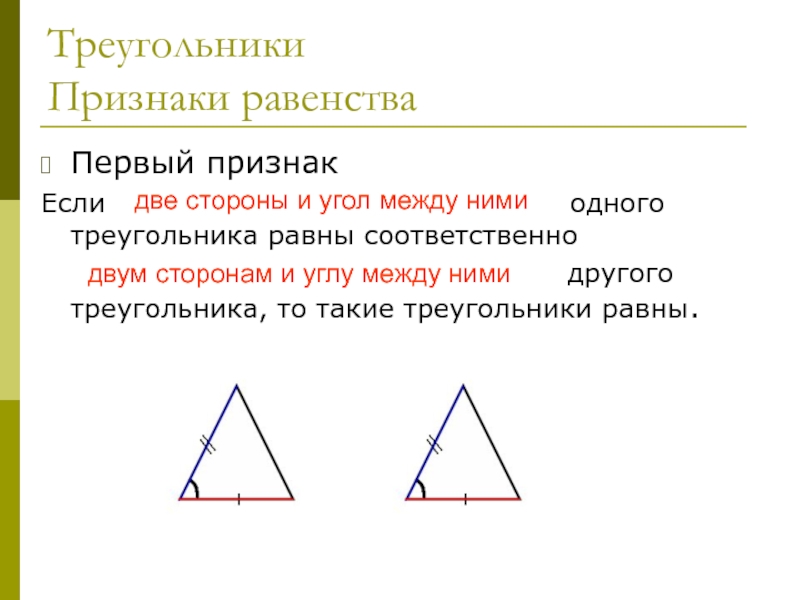
Первый признак
Если две стороны и угол между ними одного
треугольника равны соответственно
двум сторонам и углу между ними другого
треугольника, то такие треугольники равны. две стороны и угол между ними
двум сторонам и углу между ними
Слайд 24Треугольники
Признаки равенства
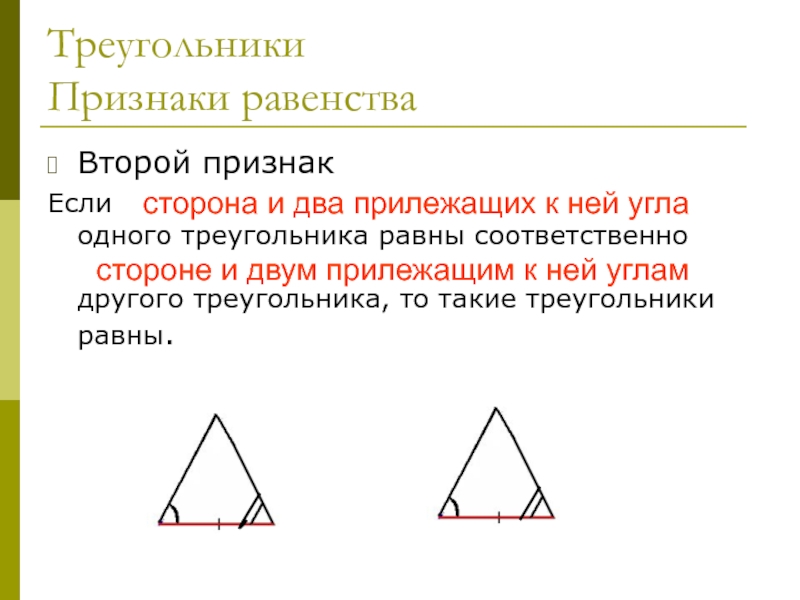
Второй признак
Если сторона и два прилежащих к ней угла
одного треугольника равны соответственно стороне и двум прилежащим к ней
углам другого треугольника, то такие треугольники равны.сторона и два прилежащих к ней угла
стороне и двум прилежащим к ней углам
Слайд 25Треугольники
Признаки равенства
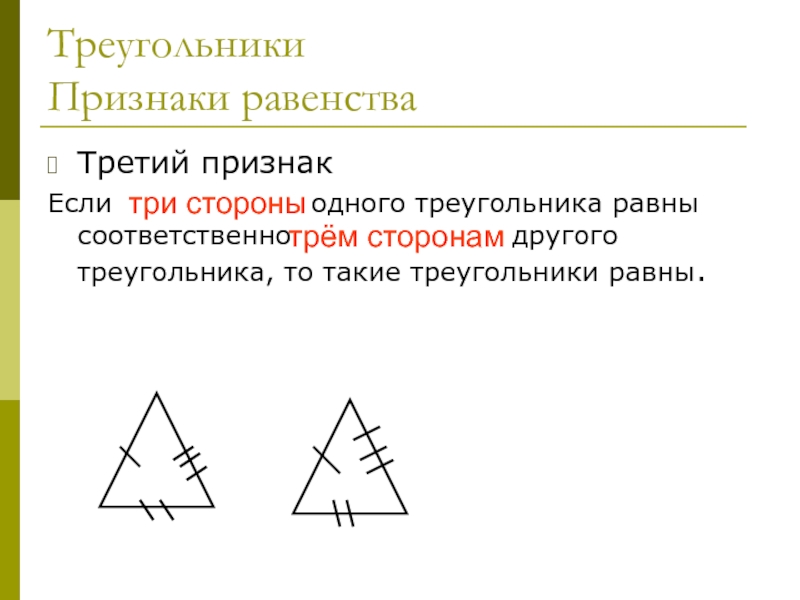
Третий признак
Если три стороны одного треугольника равны соответственно трём
сторонам другого треугольника, то такие треугольники равны.
три стороны
трём сторонам
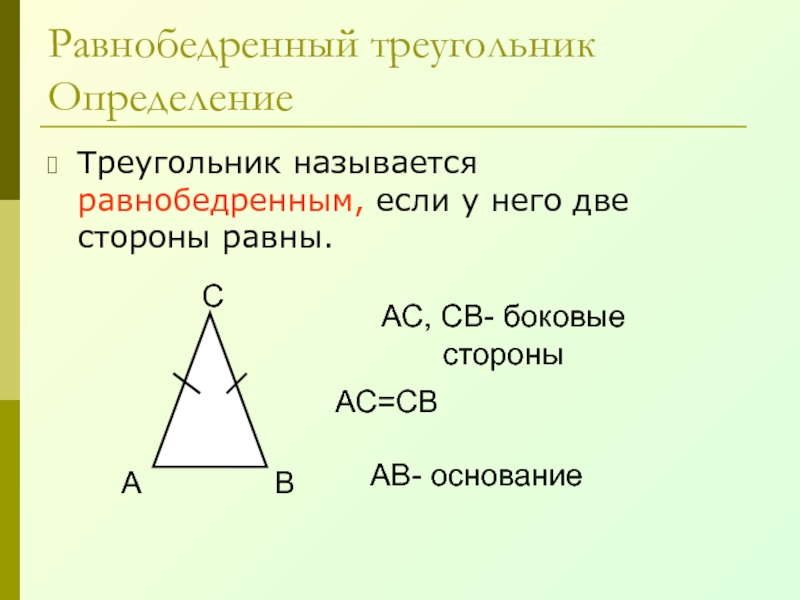
Слайд 26Равнобедренный треугольник
Определение
Треугольник называется равнобедренным, если у него две стороны равны.
А
В
С
АС,
СВ- боковые стороны
АС=СВ
АВ- основание
Слайд 27Равнобедренный треугольник
Свойства
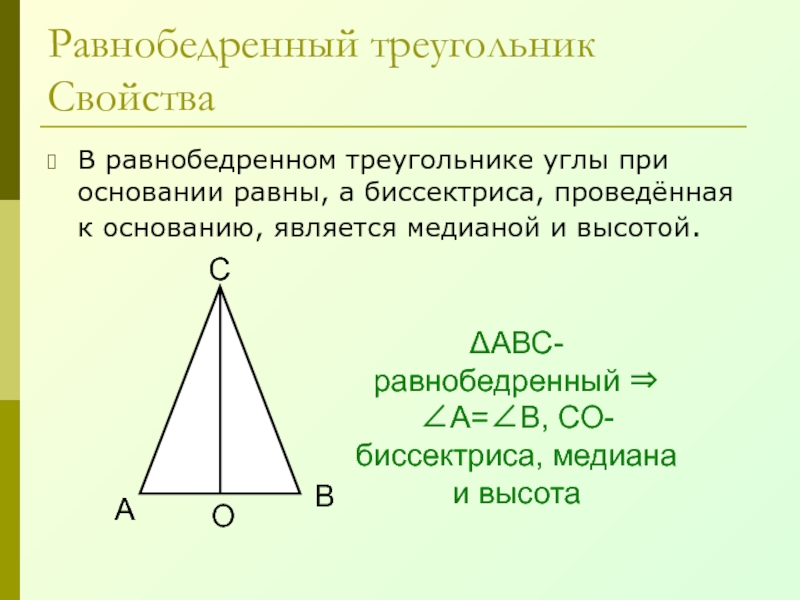
В равнобедренном треугольнике углы при основании равны, а
биссектриса, проведённая к основанию, является медианой и высотой.
А
В
С
О
ΔАВС- равнобедренный ⇒
∠А=∠В, СО- биссектриса, медиана и высота
Слайд 28Равнобедренный треугольник
Признаки
Если в треугольнике два угла равны, то он равнобедренный.
Если
в треугольнике медиана является высотой, то он равнобедренный.
Если в треугольнике
медиана является биссектрисой, то он равнобедренный.Если в треугольнике высота является биссектрисой, то он равнобедренный
Слайд 29Равносторонний треугольник
Определение
Треугольник называется равносторонним, если у него все стороны равны.
А
В
С
АС=АВ=ВС
Слайд 30Равносторонний треугольник
Свойства
В равностороннем треугольнике все углы равны.
В равностороннем треугольнике каждая
биссектриса является медианой и высотой.
В равностороннем треугольнике все три медианы
равны.
Слайд 31Равносторонний треугольник
Признаки
Если все углы в треугольнике равны, то он равносторонний.
А
В
С
∠А=∠В=∠С
⇒ ΔАВС –равносторонний
⇒ АВ=ВС=АС
Слайд 32Прямоугольный треугольник
Определение
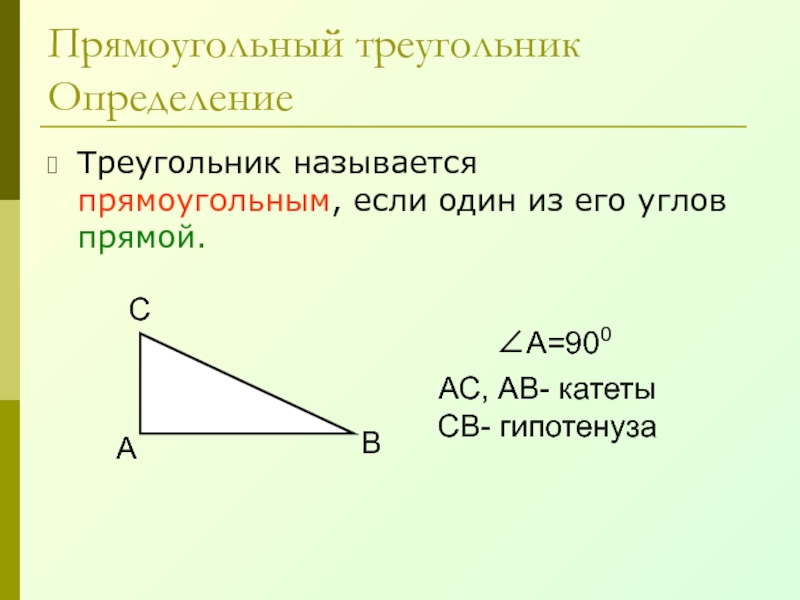
Треугольник называется прямоугольным, если один из его углов прямой.
А
В
С
∠А=900
АС,
АВ- катеты
СВ- гипотенуза
Слайд 33Прямоугольный треугольник
Признаки
Если катет и гипотенуза одного
прямоугольного треугольника соответственно равны катету и гипотенузе другого, то такие
треугольники равны.катет и гипотенуза
катету и
гипотенузе
Слайд 34Прямоугольный треугольник
Признаки
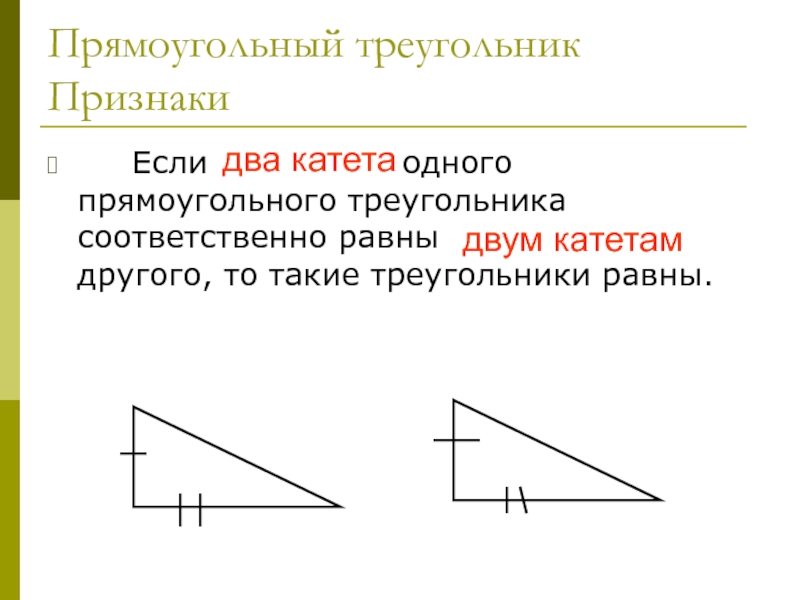
Если два катета одного прямоугольного
треугольника соответственно равны двум катетам другого, то такие треугольники равны.
два катета
двум катетам
Слайд 35Прямоугольный треугольник
Признаки
Если катет и острый угол
одного прямоугольного треугольника соответственно равны катету и острому углу другого,
то такие треугольники равны.катет и острый угол
катету и острому
углу
Слайд 36Прямоугольный треугольник
Признаки
Если гипотенуза и острый угол
одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого,
то такие треугольники равны.гипотенуза и острый угол
гипотенузе и
острому углу
Слайд 37Прямоугольный треугольник
Свойства
Катет прямоугольного треугольника, лежащий против угла 300, равен половине
гипотенузы.
А
С
В
∠А=900
∠В=300
АС=0,5ВС
Слайд 38Прямоугольный треугольник
Свойства
В прямоугольном треугольнике сумма острых углов равна 900.
А
В
С
∠А=900,
∠В+∠С=900
