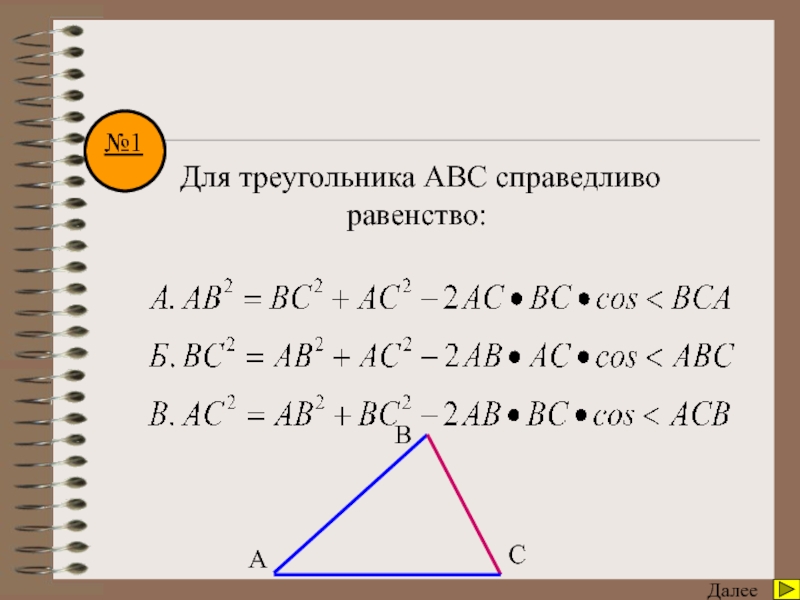
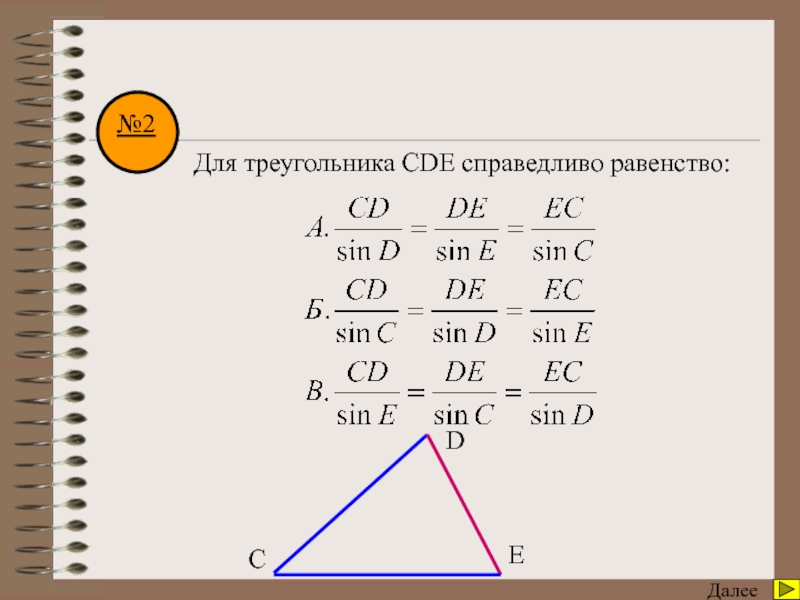
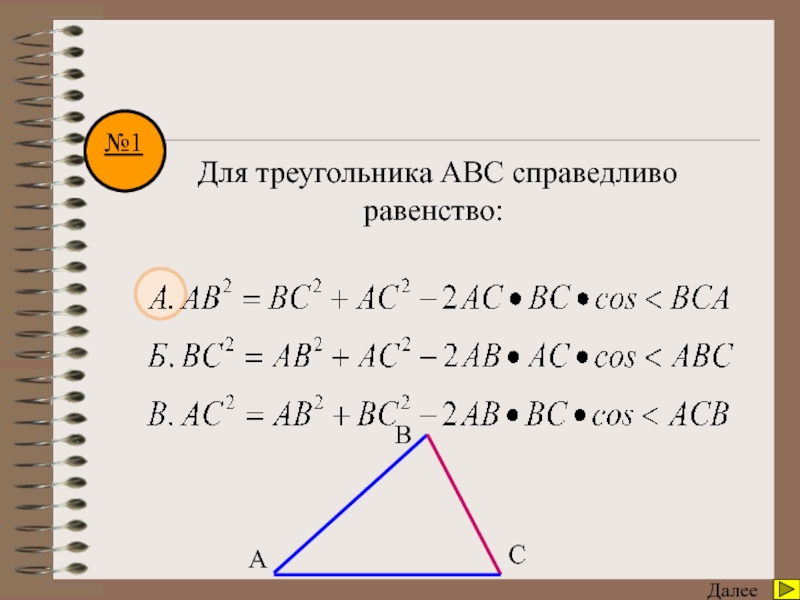
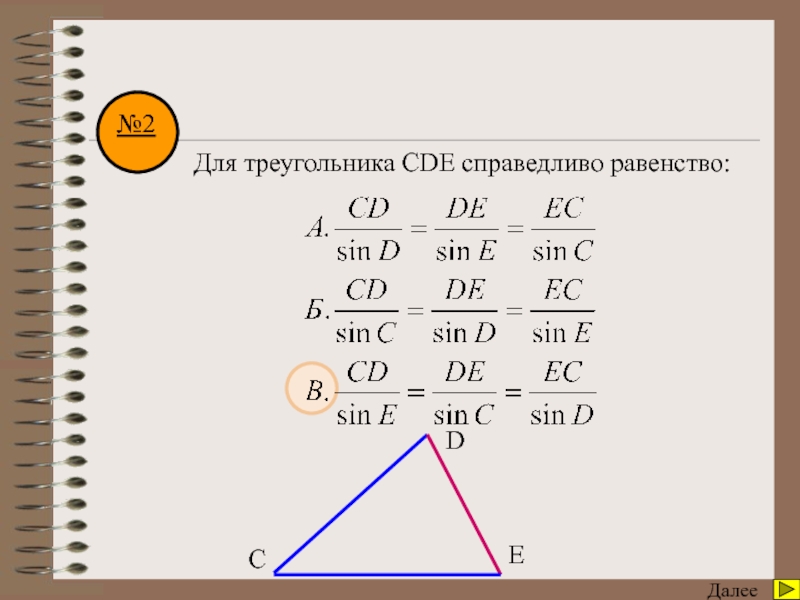
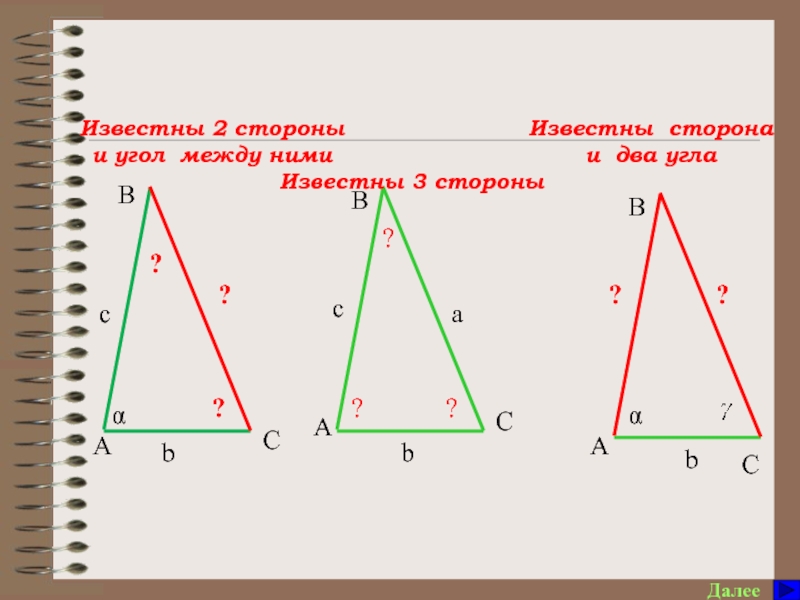
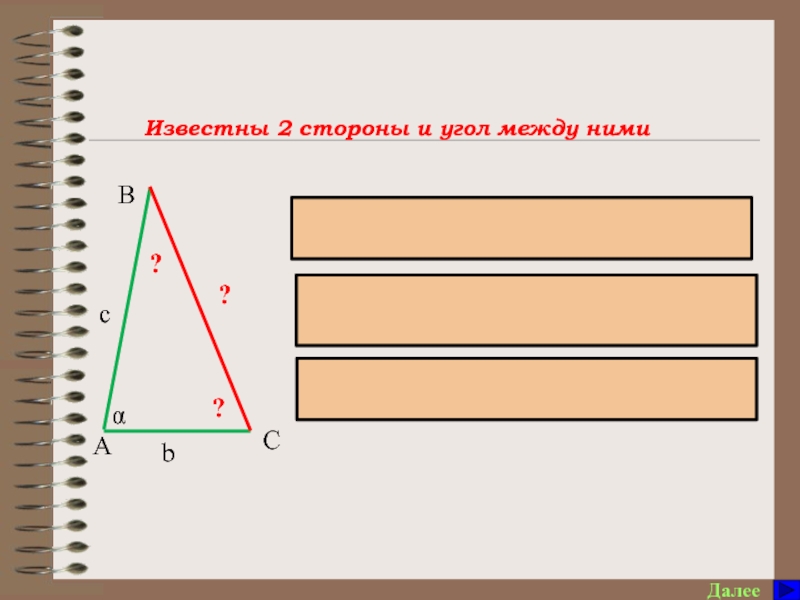
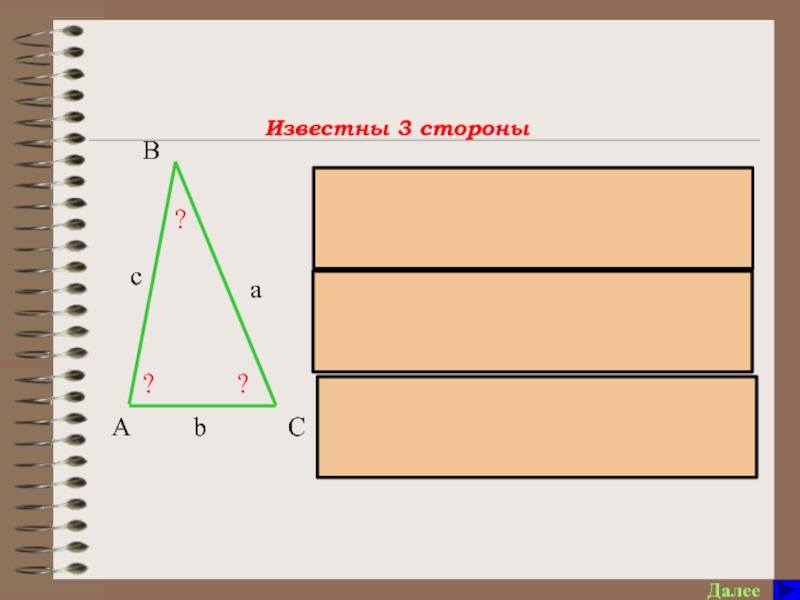
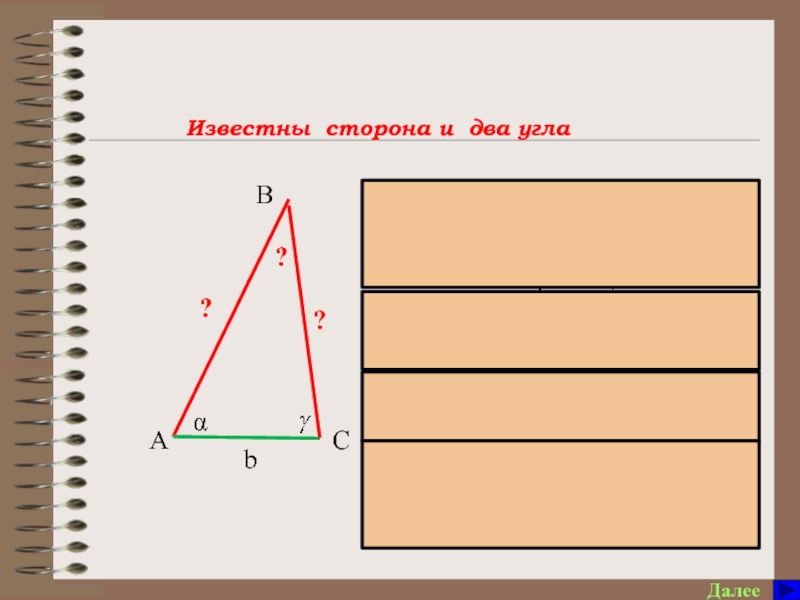
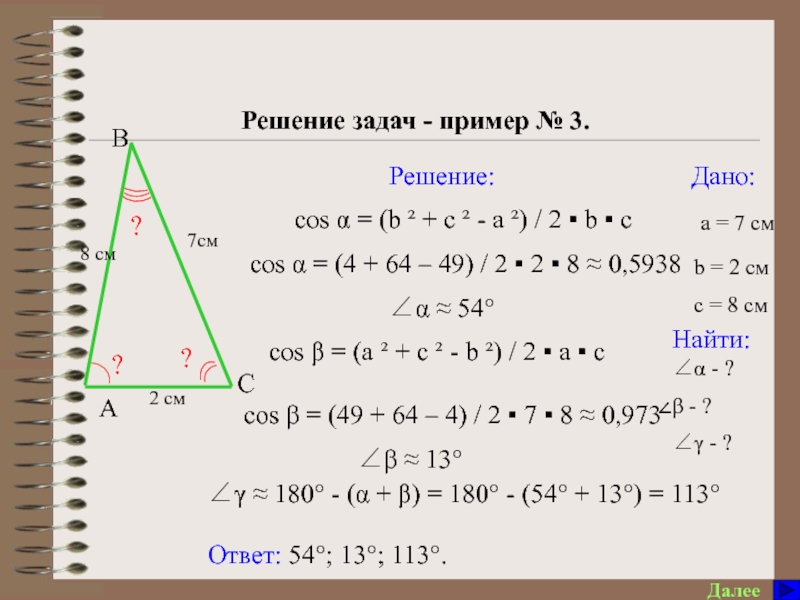
угол А треугольника АВС, если сторона АВ=с, АС=b, ВС=а.
4. Чему
равен синус тупого угла?5. Чему равен косинус тупого угла?
6. Сколько углов соответствует значению sin?
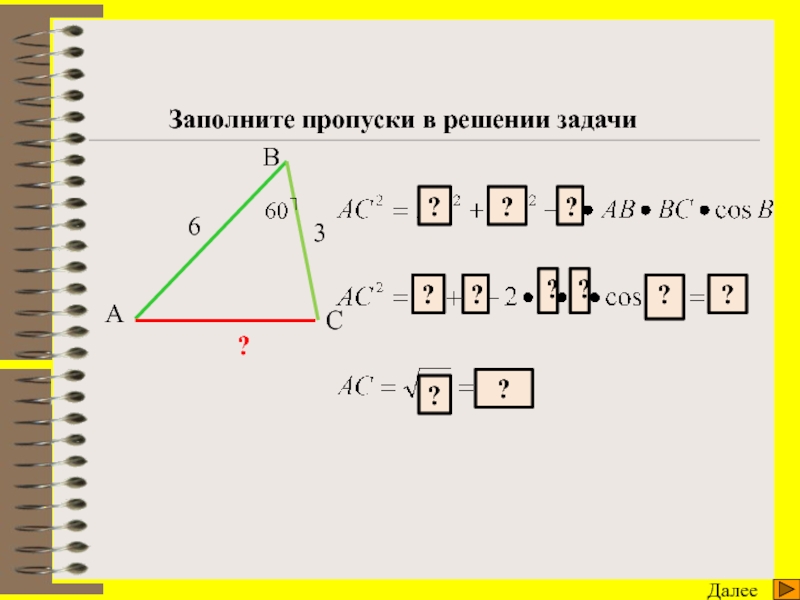
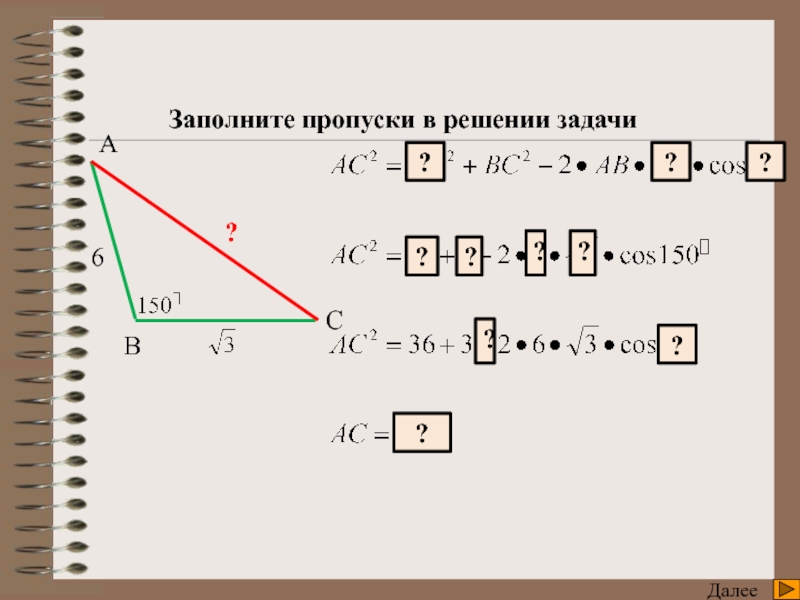
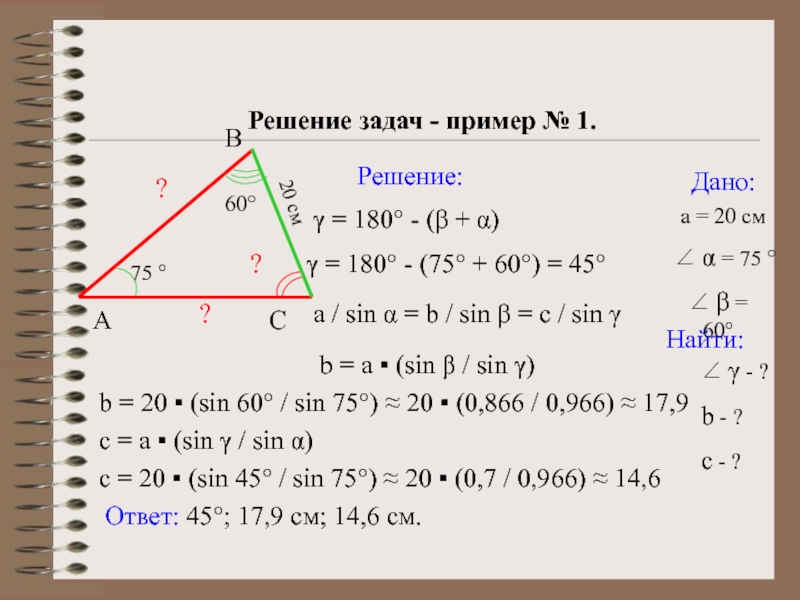
7. Что позволяет найти теорема косинусов и при каких условиях?
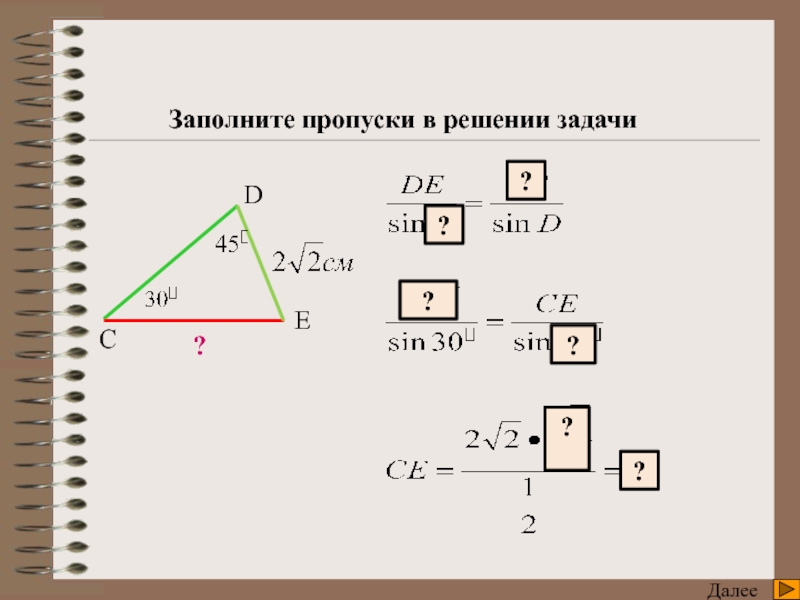
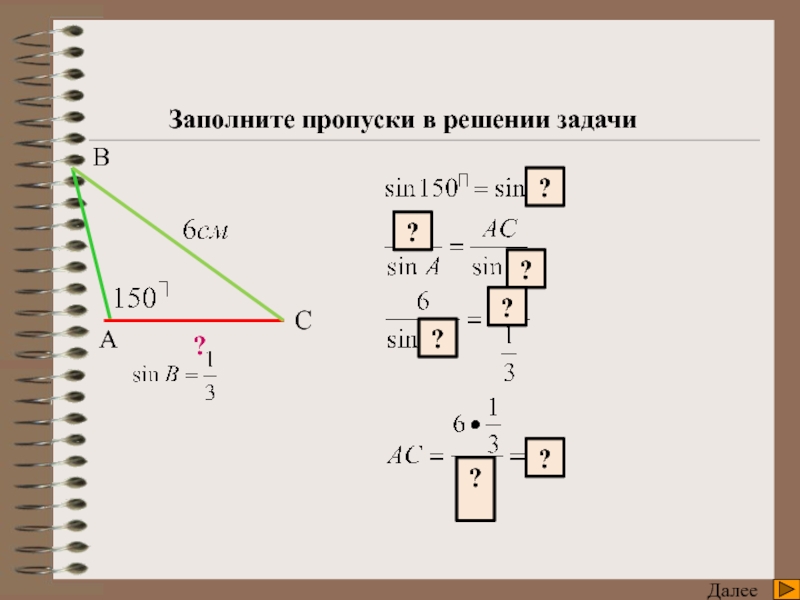
8. Что позволяет найти теорема синусов и при каких условиях?