Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Треугольники
Содержание
- 1. Треугольники
- 2. Итоговое повторение курса геометрии мы начнём с
- 3. Классификация треугольниковОстроугольныйПрямоугольныйТупоугольный РавнобедренныйРавностороннийОпределите виды треугольников
- 4. Прямоугольный Треугольник
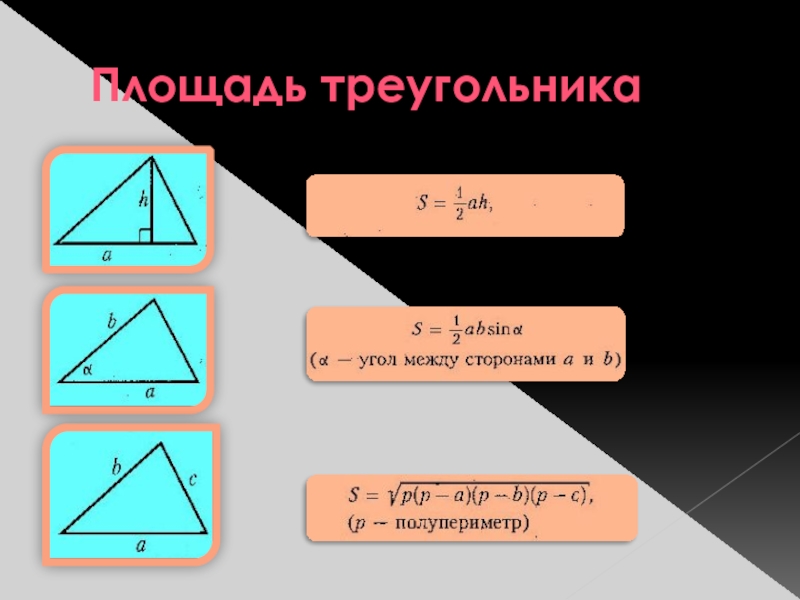
- 5. Площадь треугольника
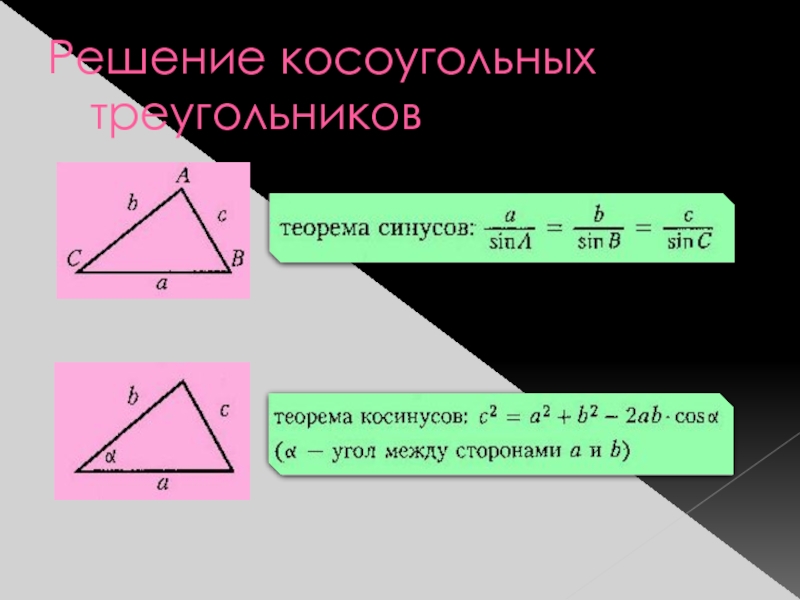
- 6. Решение косоугольных треугольников
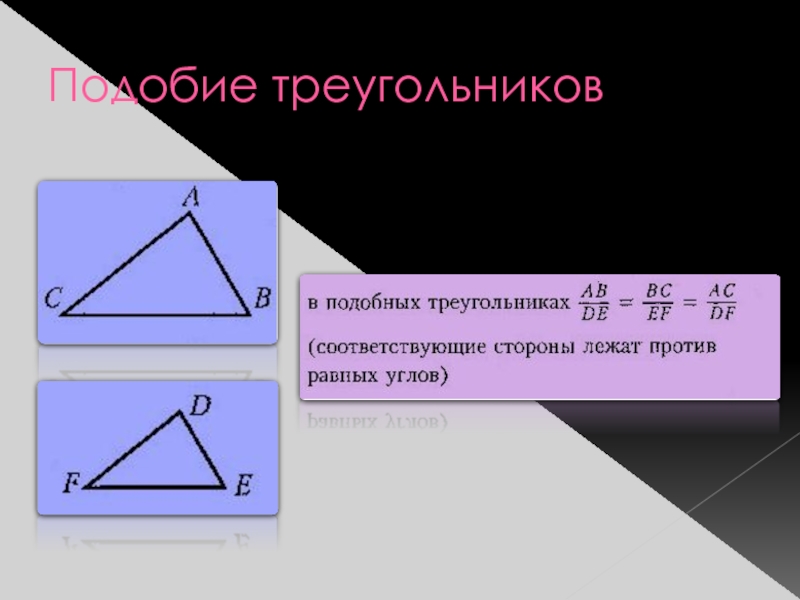
- 7. Подобие треугольников
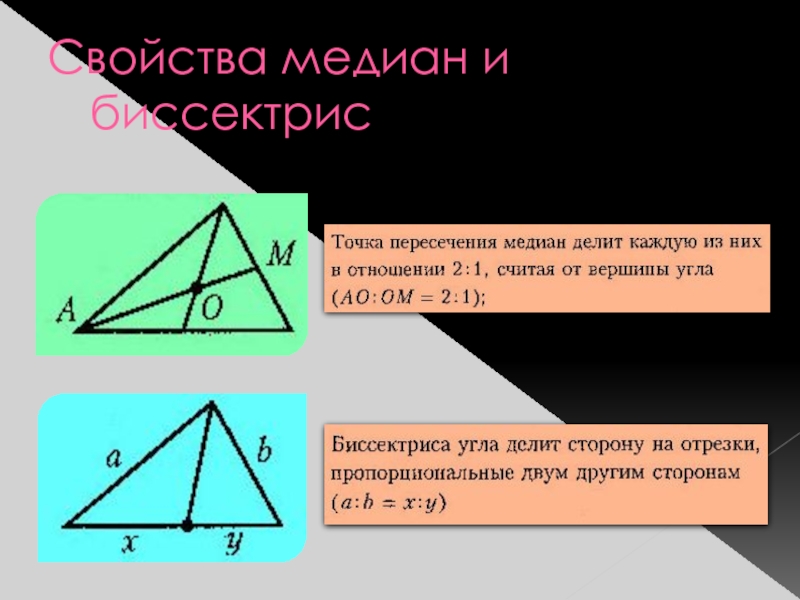
- 8. Свойства медиан и биссектрис
- 9. Задача. Найдите высоту прямоугольного треугольника, проведенную к
- 10. Задача. Из вершины В параллелограмма АВСD проведён
- 11. Задача. Дан равнобедренный треугольник АВС, АС=АВ=20, высоты
- 12. Скачать презентанцию
Итоговое повторение курса геометрии мы начнём с повторения планиметрии. Основные факты планиметрии и применяемые в ней методы можно сгруппировать по следующим темам: «Треугольники», «Четырёхугольники, многоугольники», «Окружность».Цель итогового повторения: - восстановление в
Слайды и текст этой презентации
Слайд 1ТРЕУГОЛЬНИКИ
Итоговое повторение планиметрии к ГИА
Выполнила Червина Н.П., учитель математики моу
сош №5 г. Михайловки Волгоградской области
Слайд 2Итоговое повторение курса геометрии мы начнём с повторения планиметрии. Основные
факты планиметрии и применяемые в ней методы можно сгруппировать по
следующим темам: «Треугольники», «Четырёхугольники, многоугольники», «Окружность».Цель итогового повторения:
- восстановление в памяти учащихся основного материала;
- обобщение, уточнение и систематизация знаний по планиметрии.
Тема урока: «Треугольники»
Цель урока: - повторение теоретического материала;
-обобщение навыка решения задач;
Слайд 3Классификация треугольников
Остроугольный
Прямоугольный
Тупоугольный
Равнобедренный
Равносторонний
Определите виды треугольников
Слайд 9Задача. Найдите высоту прямоугольного треугольника, проведенную к гипотенузе, если биссектриса
острого угла делит катет на отрезки, равные 2 и 4.
В2х х
4 2
А С
Решение. 1) По свойству биссектрисы
Имеем АВ:ВС=2:1, тогда, если ВС=х,
То АВ=2х, АС= , АС=6,
Тогда =6,откуда , то есть ВС= , АВ= .
2) Найдём высоту СН:
S =0,5·АС·ВС=0,5АВ·СН, откуда
СН=
Ответ: 3
Слайд 10Задача. Из вершины В параллелограмма АВСD проведён луч, который пересекает
СD в (·)N и диагональ АС в (·)Т. Площадь треугольника ВСТ
равна 12,а СТN-8. Найти площадь параллелограмма АВСD.Решение: 12=1∕2∙ВТ·h, ВТ=24∕ h и
8=1∕ 2·ТN∙h, ТN=16∕ h,
ВТ:ТN=24:16=3:2.Треугольники
АВТ и СТN подобны(по двум углам), значит отношение их площадей равно kⁿ, где k=2, т.е.
9∕4. SАВТ:SСТN=9:4, SАВТ=8∙9:4=18,
SАВС=18+12=30,
SАВСD=30·2=60
Ответ: 60
В С
Т
N
А D
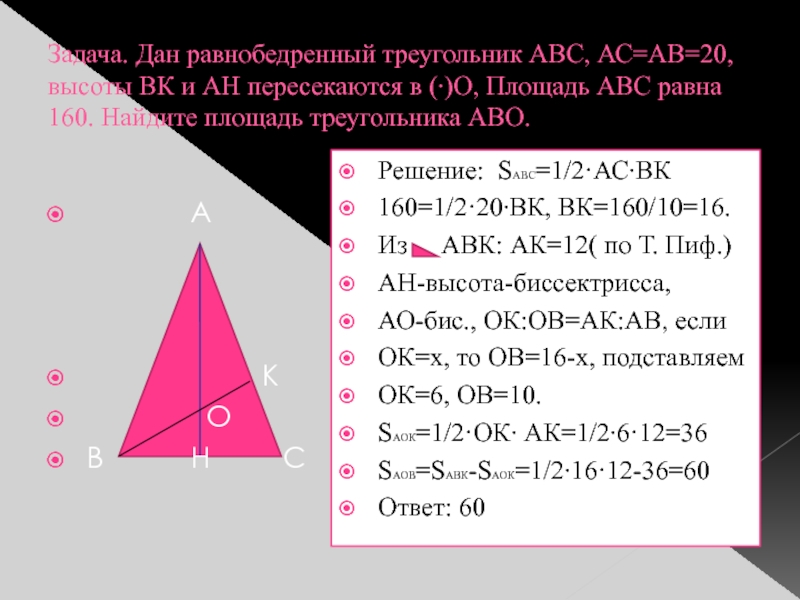
Слайд 11Задача. Дан равнобедренный треугольник АВС, АС=АВ=20, высоты ВК и АН пересекаются
в (∙)О, Площадь АВС равна
160. Найдите площадь треугольника АВО.
Решение: SАВС=1/2·АС∙ВК
160=1/2·20∙ВК,
ВК=160/10=16.Из АВК: АК=12( по Т. Пиф.)
АН-высота-биссектрисса,
АО-бис., ОК:ОВ=АК:АВ, если
ОК=х, то ОВ=16-х, подставляем
ОК=6, ОВ=10.
SАОК=1/2·ОК∙ АК=1/2∙6·12=36
SАОВ=SАВК-SАОК=1/2∙16·12-36=60
Ответ: 60
А
К
О
В Н С
