Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразования на плоскости
Содержание
- 1. Преобразования на плоскости
- 2. О симметрия! Гимн тебе пою! Тебя
- 3. Симметрия (греч.) - соразмерность, пропорциональность, одинаковость в расположении частей.
- 4. Виды симметрии Симметрия относительно прямойСимметрия относительно точкиПоворотСимметрия в природеСимметрия в архитектуре
- 5. Две точки А и А1 называются симметричными
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Являются ли данные точки симметричными ?ММ1mСDbBВ1аРисунок 1Рисунок 2Рисунок 3
- 10. Сколько осей симметрии имеет:ОтрезокПрямаяЛучАВаОЕ однамножествоНи однойЗадачи:
- 11. Какие из этих фигур имеют ось симметрии? Сколько осей симметрии имеет каждая фигура?56311224Бесконечно много
- 12. Две точки А и А1 называются симметричными
- 13. Слайд 13
- 14. О
- 15. О
- 16. Слайд 16
- 17. Являются ли точки симметричными относительно данной точки?Рисунок 1Рисунок 2Рисунок 3М1ВВ1ОМАА1ОС
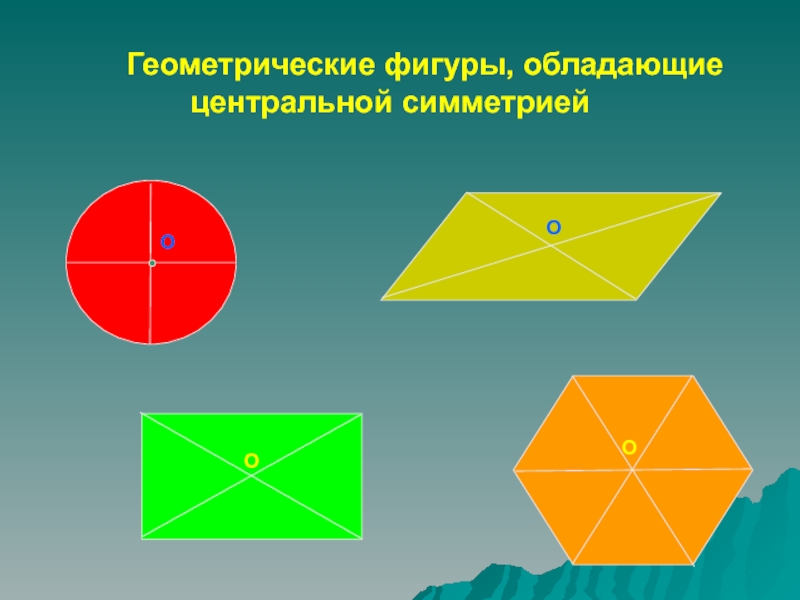
- 18. ОООО Геометрические фигуры, обладающие центральной симметрией
- 19. Имеют ли центр симметрии:ОтрезокПрямаяЛучЗадачиОодинмножествоНи одногоОО1О2
- 20. АВСА1В1 Начертите треугольник АВС Постройте симметричный ему треугольник относительно вершины С.
- 21. Постройте и проверьте себя
- 22. Начертите
- 23. Поворот Поворот задается: - центром поворота
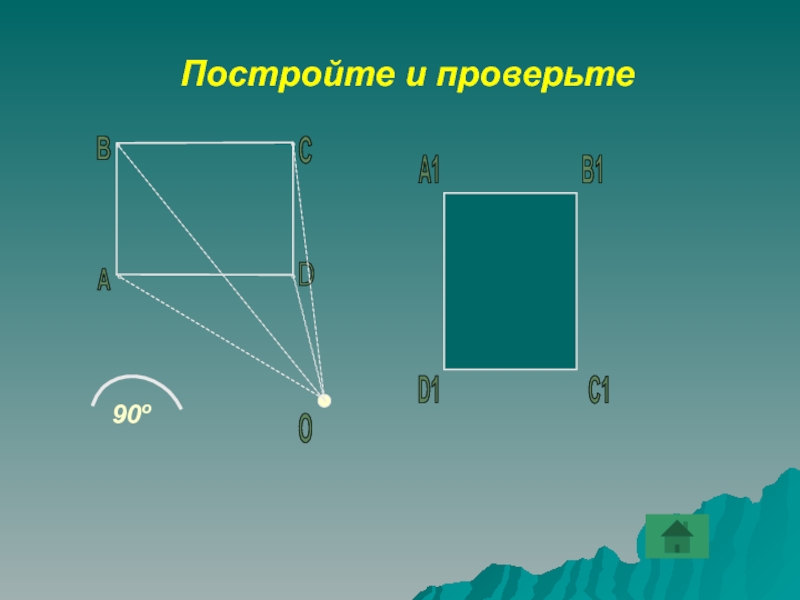
- 24. В1С1D1А1DПостройте и проверьте АВСО90о
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Симметрия в балетеЗнаменитые фуэте, когда балерина вращается
- 29. Винтовая симметрия Листья располагаются на стволе по винтовой линии, чтобы заслонять друг от друга солнечный свет.
- 30. Казанский собор
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. С какими новыми понятиями познакомились?Что нового узнали
- 37. Спасибо за внимание!
- 38. Скачать презентанцию
О симметрия! Гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой башне, в малой мошке, Ты в елочке, что у лесной дорожки. С тобою в дружбе и тюльпан,
Слайды и текст этой презентации
Слайд 4Виды симметрии
Симметрия относительно прямой
Симметрия относительно точки
Поворот
Симметрия в природе
Симметрия в
архитектуре
Слайд 5Две точки А и А1 называются симметричными относительно прямой а,
если эта прямая проходит через середину отрезка АА1 и перпендикулярна
к немуа – ось симметрии
Слайд 11Какие из этих фигур имеют ось симметрии?
Сколько осей
симметрии имеет каждая фигура?
5
6
3
1
1
2
2
4
Бесконечно много
Слайд 12Две точки А и А1 называются симметричными относительно точки О,
если О – середина отрезка АА1
О - центр симметрии
Слайд 17Являются ли точки симметричными относительно данной точки?
Рисунок 1
Рисунок 2
Рисунок 3
М1
В
В1
О
М
А
А1
О
С
Слайд 20А
В
С
А1
В1
Начертите треугольник АВС Постройте
симметричный ему треугольник относительно вершины С.
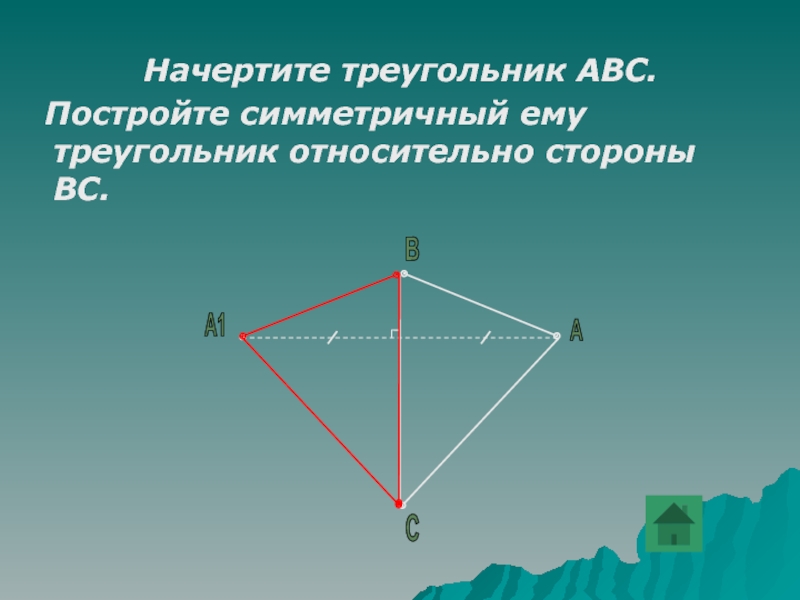
Слайд 22 Начертите треугольник АВС.
Постройте симметричный ему треугольник относительно стороны ВС.
А
В
А1
С
Слайд 23Поворот
Поворот задается:
- центром поворота
- углом поворота (90о)
-
направлением (по часовой стрелке или против)
А
В
С
О
А1
В1
С1
Слайд 28Симметрия в балете
Знаменитые фуэте, когда балерина вращается на одной ножке
6 раз, 12, …, 32 раза!
Их повторяемость рождает эстетический
эффект, служащий достойным завершением танца!Слайд 29Винтовая симметрия
Листья располагаются на стволе по винтовой линии, чтобы
заслонять друг от друга солнечный свет.
Слайд 33
Диссимметрия –
это частичное отсутствие симметрии, её
расстройство, выраженное в наличии одних симметричных свойств и отсутствии других. Слайд 36С какими новыми понятиями познакомились?
Что нового узнали о геометрических фигурах?
Приведите
примеры геометрических фигур, обладающих осевой симметрией.
Приведите пример фигур, обладающих центральной
симметрией.Приведите примеры предметов
из окружающей жизни, обладающих
одной или двумя видами симметрии.
Итог урока