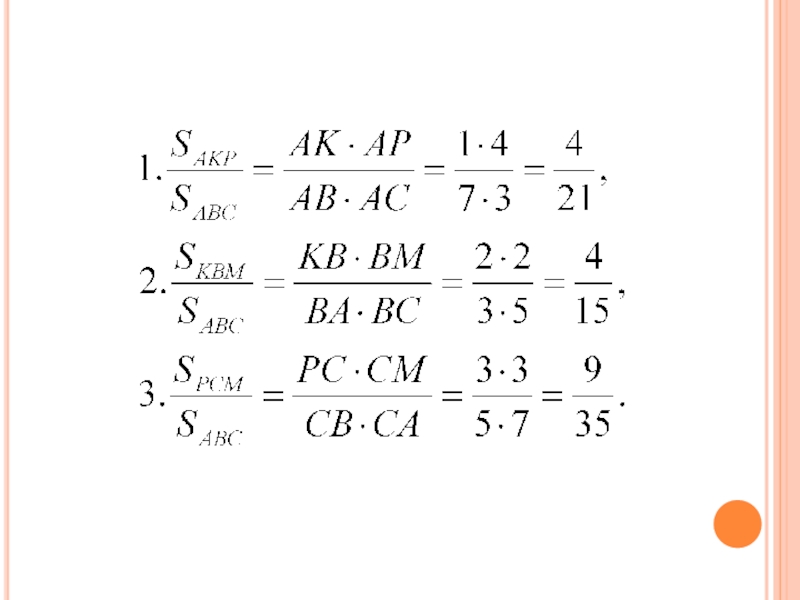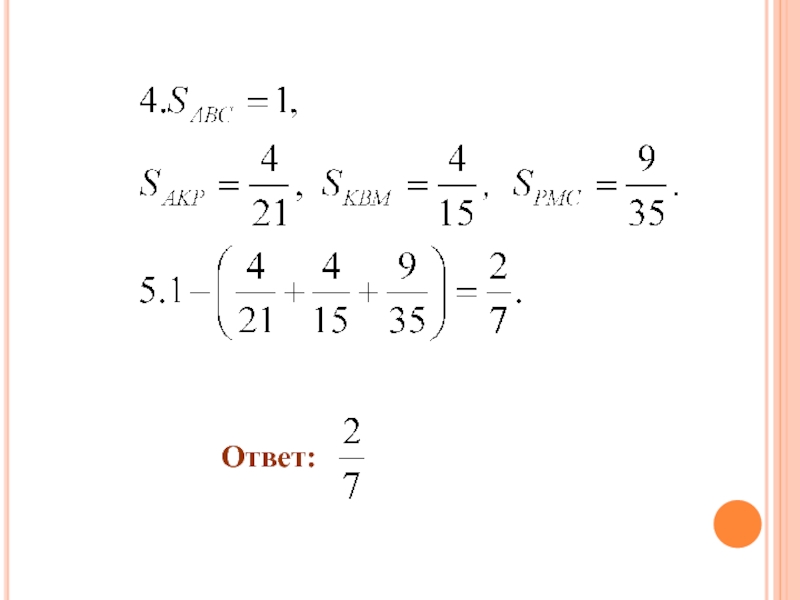Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение планиметрических задач (метод площадей) 8-9 классы
Содержание
- 1. Решение планиметрических задач (метод площадей) 8-9 классы
- 2. Наши знания никогда не могут иметь конца
- 3. Свойства площадей:Площадь фигуры является неотрицательным числом.Площади равных
- 4. АОтвет: 22
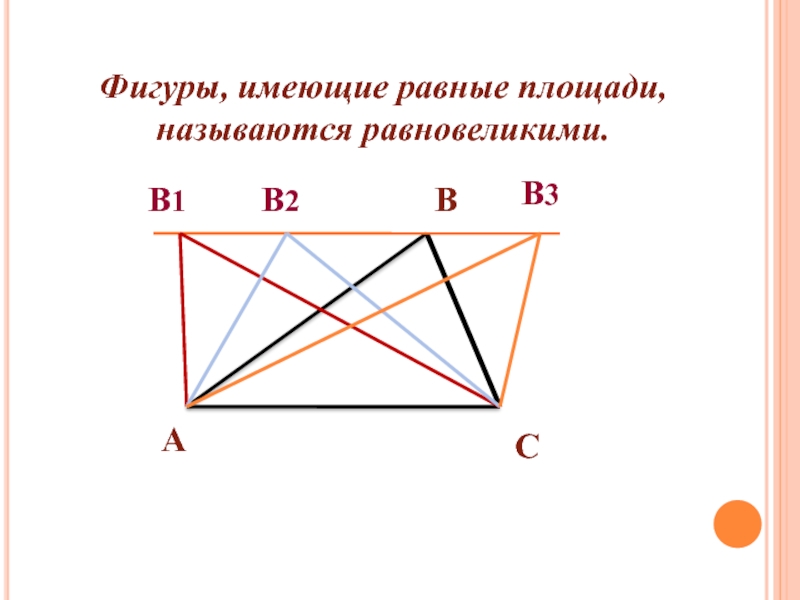
- 5. Фигуры, имеющие равные площади, называются равновеликими.В1В2В3
- 6. Равные фигуры всегда равновелики, но равновеликие фигуры могут быть неравными.
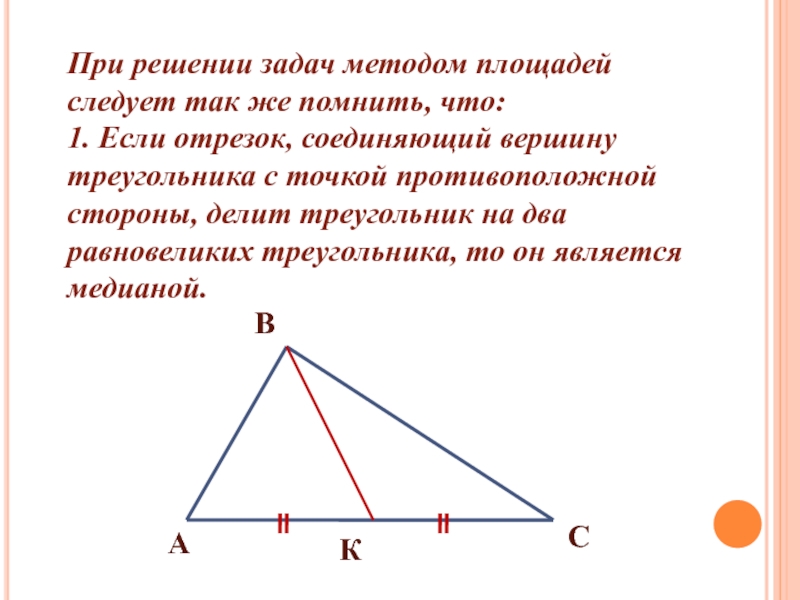
- 7. При решении задач методом площадей следует так
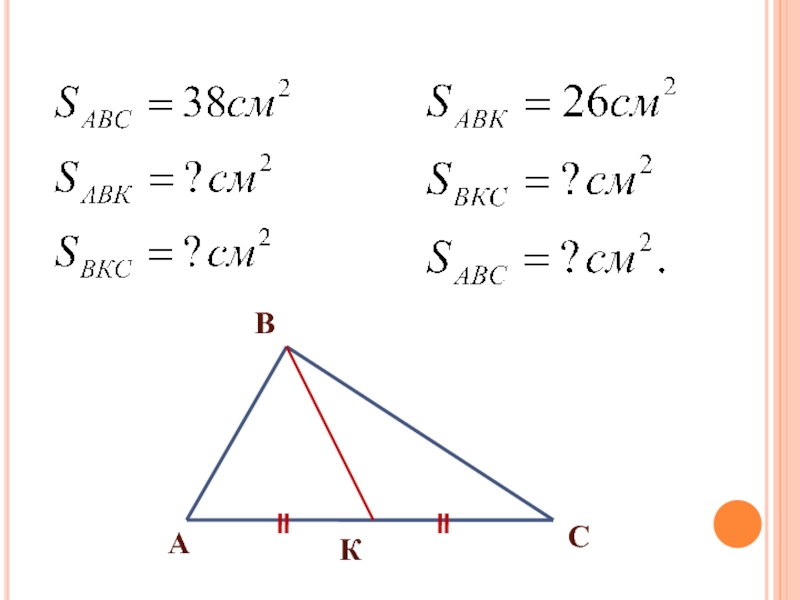
- 8. АСВК
- 9. При решении задач методом площадей следует так
- 10. АСВКМNO
- 11. При решении задач методом площадей следует так
- 12. Слайд 12
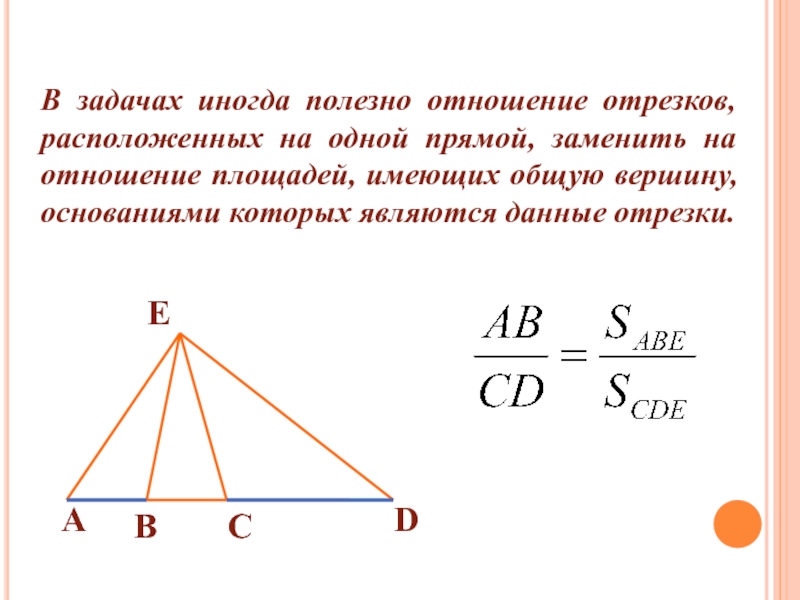
- 13. В задачах иногда полезно отношение отрезков, расположенных
- 14. Слайд 14
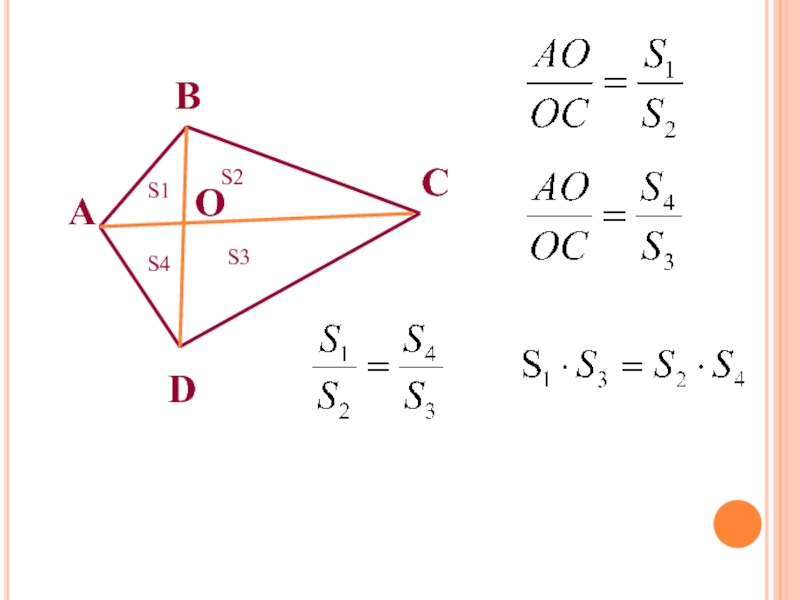
- 15. АВСDОS1S2S3S4
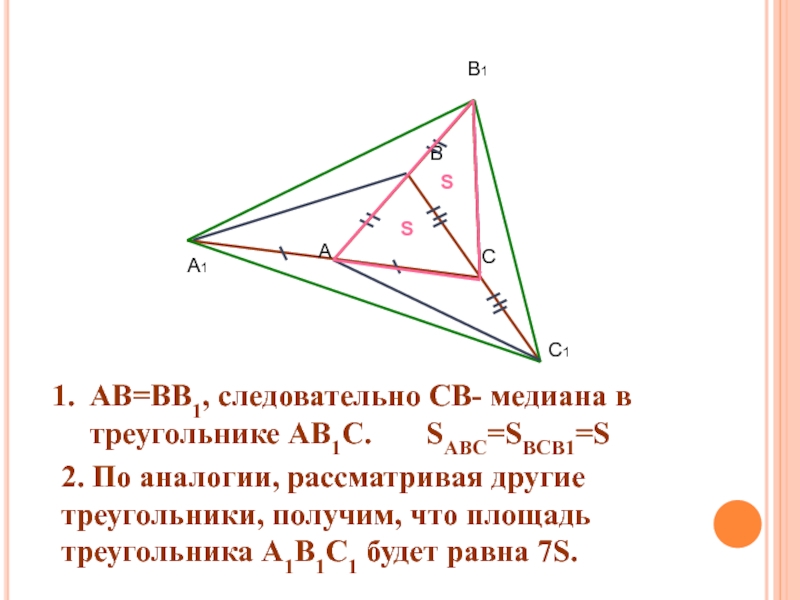
- 16. Дано: АВС- треугольникАВ=ВВ1, ВС=СС1, СА=АА1,SABC=SНайти: SA1B1C1Задача.Каждая сторона
- 17. Выполним дополнительное построение. Соединим точки А, В
- 18. АВ=ВВ1, следовательно СВ- медиана в треугольнике АВ1С.
- 19. Задача.Докажите, что если площади двух треугольников, прилежащих
- 20. Дано: АВСD- трапеция, DB пересекает АС в точке О, SBOC=p2, SAOD=q2Доказать: SABCD=(p+q)2Op2q2
- 21. Задача.Вершина С параллелограмма АВСD соединена с точкой
- 22. 129Дано: АВСD- параллелограмм,СК пересекает DB в точке
- 23. Площади двух треугольников, имеющих по равному углу, относятся, как произведения сторон, заключающих эти углы.АВС
- 24. Задача. На сторонах AB,
- 25. АВСMРK123342Дано: АВС- треугольник.Найти SKMP
- 26. Слайд 26
- 27. Ответ:
- 28. «Геометрия является самым могущественным средством для изощрения
- 29. Скачать презентанцию
Наши знания никогда не могут иметь конца именно потому, что предмет познания бесконечен.
Слайды и текст этой презентации
Слайд 1РЕШЕНИИ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ
(метод площадей)
Болдырева Татьяна Викторовна
Учитель математики
МАОУ- Лицей №62
г.Саратов
Слайд 2Наши знания никогда не могут иметь конца именно потому, что
предмет познания бесконечен.
Блез Паскаль.
Слайд 3Свойства площадей:
Площадь фигуры является неотрицательным числом.
Площади равных фигур равны.
Если фигура
разделена на части, то площадь всей фигуры равна сумме площадей
образовавшихся частей.
Слайд 7При решении задач методом площадей следует так же помнить, что:
1.
Если отрезок, соединяющий вершину треугольника с точкой противоположной стороны, делит
треугольник на два равновеликих треугольника, то он является медианой.А
С
В
К
Слайд 9При решении задач методом площадей следует так же помнить, что:
2.
Медианы треугольника делят его на шесть равновеликих треугольников.
А
С
В
К
М
N
O
Слайд 11При решении задач методом площадей следует так же помнить, что:
3.
Диагонали трапеции делят ее на четыре треугольника. Треугольники, прилежащие к
боковым сторонам, равновелики.
Слайд 13В задачах иногда полезно отношение отрезков, расположенных на одной прямой,
заменить на отношение площадей, имеющих общую вершину, основаниями которых являются
данные отрезки.
Слайд 16Дано:
АВС- треугольник
АВ=ВВ1, ВС=СС1, СА=АА1,
SABC=S
Найти: SA1B1C1
Задача.
Каждая сторона треугольника АВС продолжена
на свою длину так, что точка В- середина АВ1, С-
середина ВС1, А- середина СА1. Площадь треугольника АВС равна S. Найдите площадь треугольника А1В1С1.
Слайд 17Выполним дополнительное построение. Соединим точки А, В и С с
вершинами полученного треугольника А1, В1 и С1.
Слайд 18АВ=ВВ1, следовательно СВ- медиана в треугольнике АВ1С.
SABC=SBCB1=S
S
S
2. По аналогии, рассматривая другие треугольники, получим, что площадь треугольника
А1В1С1 будет равна 7S.
Слайд 19Задача.
Докажите, что если площади двух треугольников, прилежащих к основаниям трапеции
и образуемых пересечением ее диагоналей, равны соответственно
и , то площадь всей трапеции равна.
Слайд 20Дано:
АВСD- трапеция,
DB пересекает АС в точке О,
SBOC=p2,
SAOD=q2
Доказать:
SABCD=(p+q)2
O
p2
q2
Слайд 21Задача.
Вершина С параллелограмма АВСD соединена с точкой K на стороне
AD. Отрезок СК пересекает диагональ BD в точке N. Площадь
треугольника CDN равна 12, а площадь треугольника DKN равна 9. Найдите площадь параллелограмма ABCD.
Слайд 2212
9
Дано:
АВСD- параллелограмм,
СК пересекает DB в точке N,
SDNC=12, SDKN=9.
Найти: SABCD
Выполним
дополнительное построение КВ.
DKBC- трапеция, следовательно, SKNB=SDNC=12.
2. SNBC=x,
9x=144, x=16.3. SDBC=28, SABCD=56.
12
x
Слайд 23
Площади двух треугольников, имеющих по равному углу, относятся, как произведения
сторон, заключающих эти углы.
А
В
С
Слайд 24 Задача.
На сторонах AB, BC и СА
треугольника АВС взяты точки К, M и Р так, что
АК:КВ=1:2, ВМ:МС=2:3, СР:РА=3:4. Площадь треугольника АВС равна 1. Найдите площадь треугольника КMР.
Слайд 28«Геометрия является самым могущественным средством для изощрения наших умственных способностей
и дает нам возможность правильно мыслить и рассуждать».
Галилео Галилей
