Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямоугольник и его свойства
Содержание
- 1. Прямоугольник и его свойства
- 2. I этап Воспроизвести в тетрадях
- 3. I I этап1. Какая фигура называется четырехуголь-ником?2.Дайте
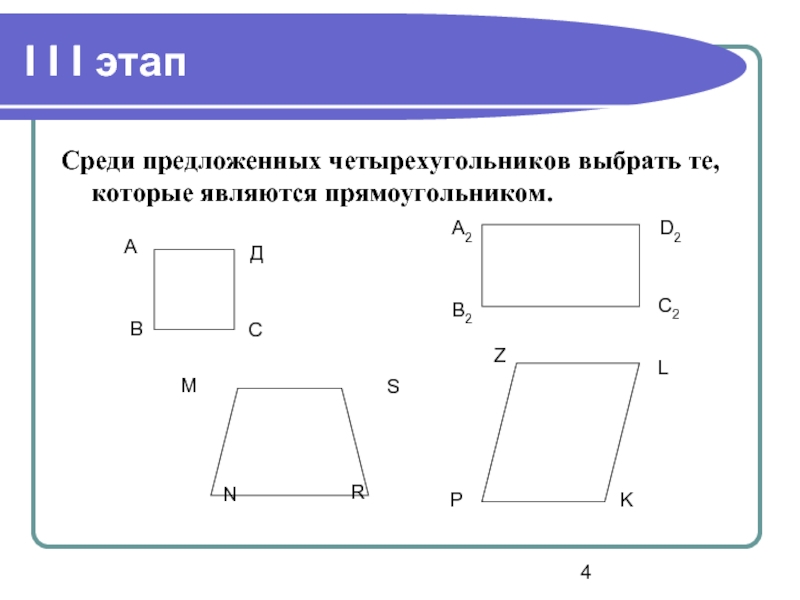
- 4. I I I этапСреди предложенных четырехугольников выбрать те, которые являются прямоугольником.АВСДА2В2С2D2MNRSZPKL
- 5. 2.Что можно сказать о градусной мере
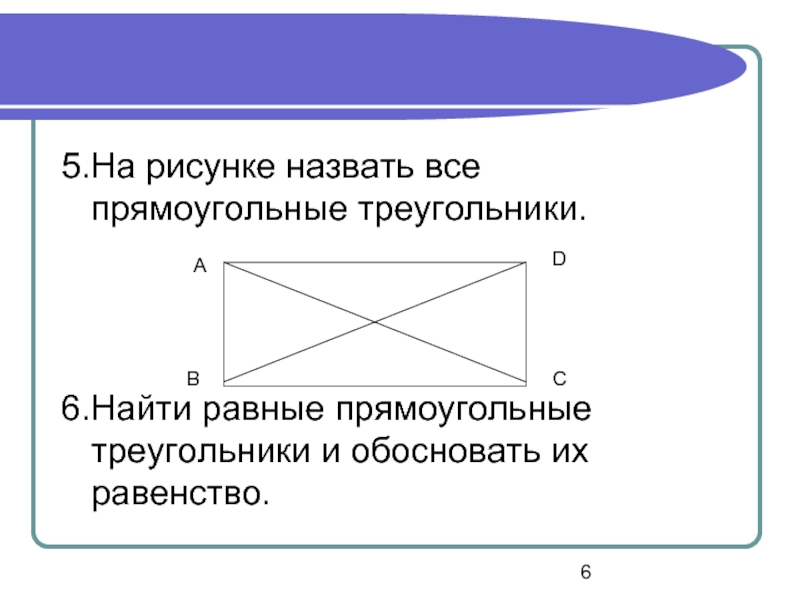
- 6. 5.На рисунке назвать все прямоугольные треугольники.6.Найти равные прямоугольные треугольники и обосновать их равенство.ABCD
- 7. 7.Какое заключение можно сделать о диагоналях прямоугольника?8.Сформулируйте
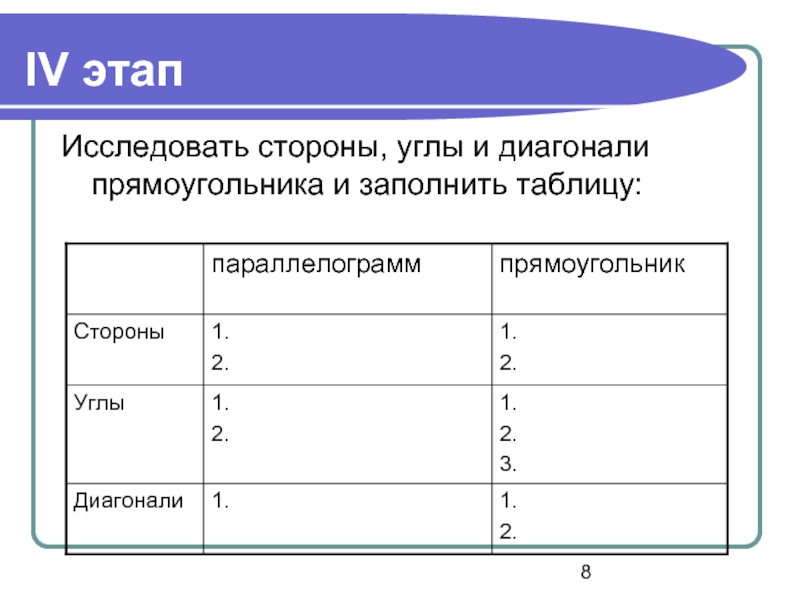
- 8. IV этап Исследовать стороны, углы и диагонали прямоугольника и заполнить таблицу:
- 9. Решение задач:Задача I команде:Докажите, что диагонали прямоугольника
- 10. Выводы:Свойство прямоугольника: Диагонали прямоугольника равны.Признак прямоугольника: Если у параллелограмма диагонали равны, то он является прямоугольником.
- 11. VI этап Домашнее задание: п.45, вопросы 12,13 стр. 115, № 399,№ 401 (а), №403.
- 12. Скачать презентанцию
I этап Воспроизвести в тетрадях для самостоятельных работ опорный конспект по материалу предыдущего урока «Параллелограмм и его свойства».
Слайды и текст этой презентации
Слайд 1Тема урока
Прямоугольник и его свойства
8 класс
Учитель Н.Г.Родионова,
МОУ СОШ №3,
г.Боготол,
Красноярский край
Слайд 2 I этап
Воспроизвести в тетрадях для самостоятельных работ
опорный конспект по материалу предыдущего урока «Параллелограмм и его свойства».
Слайд 3I I этап
1. Какая фигура называется четырехуголь-ником?
2.Дайте определение параллелограмма.
3.Является ли
параллелограмм выпуклым четырехугольником?
4.Каким свойством обладают противопо-ложные стороны параллелограмма?
5.Каким свойством обладают
противопо-ложные углы параллелограмма?6.Каким свойством обладают диагонали параллелограмма?
7.Сформулируйте признаки равенства прямоугольных треугольников.
Слайд 4I I I этап
Среди предложенных четырехугольников выбрать те, которые являются
прямоугольником.
А
В
С
Д
А2
В2
С2
D2
M
N
R
S
Z
P
K
L
Слайд 5
2.Что можно сказать о градусной мере каждого угла прямоугольника?
3.Доказать,
что у прямоугольника А2В2 С2Д2 стороны А2В2 и С2Д2;
А2Д2 и В2С2 – параллельны.4. Можно ли утверждать, что прямоугольник – параллелограмм?
Слайд 6
5.На рисунке назвать все прямоугольные треугольники.
6.Найти равные прямоугольные треугольники
и обосновать их равенство.
A
B
C
D
Слайд 7
7.Какое заключение можно сделать о диагоналях прямоугольника?
8.Сформулируйте свойства, относящиеся одновременно
и к параллелограмму, и к прямоугольнику, и свойства, относящиеся только
к прямоугольнику.Слайд 9Решение задач:
Задача I команде:
Докажите, что диагонали прямоугольника равны.
Задача I I
команде:
Докажите, что если у параллелограмма диагонали равны, то он является
прямоугольником.Слайд 10Выводы:
Свойство прямоугольника:
Диагонали прямоугольника равны.
Признак прямоугольника:
Если у параллелограмма диагонали
равны, то он является прямоугольником.
Теги