Теорема о прямой, перпендикулярной к плоскости 10 класс

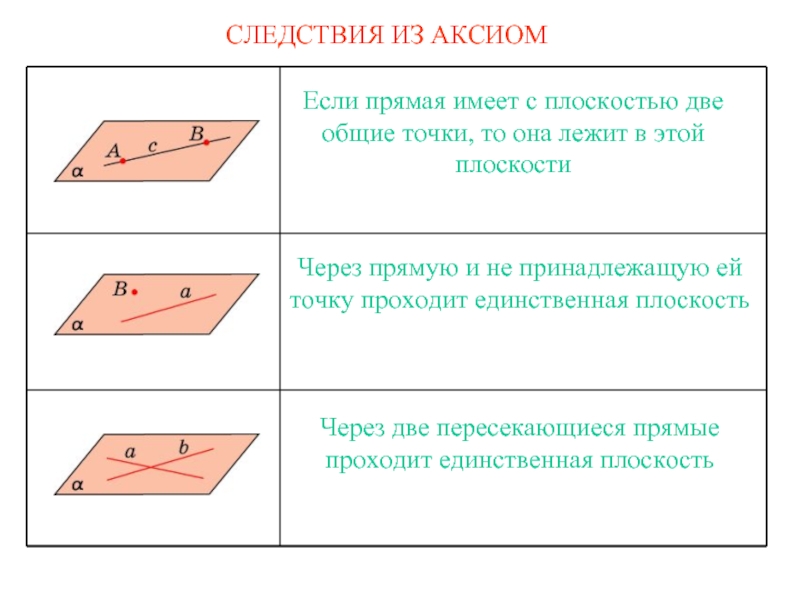
которая проходит через точку М и которая ┴ прямой а. Через прямую а проведем плоскости α

и β так, что точка М  ∈ плоскости α. Плоскости α и β пересекаются по прямой а. В плоскости α через точку М проведем перпендикуляр MN (или р) к прямой а, . В плоскости β из точки N восстановим перпендикуляр q к прямой а. Прямые р и q пересекаются, пусть через них проходит плоскость γ. Получаем, что прямая а перпендикулярна двум пересекающимся прямым р и q из плоскости γ. Значит, по признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости γ.

Задача 133

и притом только одна.

что через точку М проходит единственная прямая с, перпендикулярная плоскости α.
Проведем прямую а в плоскости α

(см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b– линия пересечения плоскостей α и γ.

как прямая а перпендикулярна плоскости γ, а значит, и прямой с, лежащей в плоскости

γ). Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.
Предположим, что существует прямая с1, проходящая через точку М и перпендикулярная плоскости α. Получаем, что прямые с и с1 перпендикулярны плоскости α. Значит, прямые с и с1 параллельны. Но по построению прямые с и с1 пересекаются в точке М. Получили противоречие. Значит, существует единственная прямая, проходящая через точку М и перпендикулярная плоскости α, что и требовалось доказать.