Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Предмет стереометрия. Аксиомы стереометрии 10 класс
Содержание
- 1. Предмет стереометрия. Аксиомы стереометрии 10 класс
- 2. Слайд 2
- 3. Стереометрия- это раздел геометрии, в котором изучаются свойства фигур в пространстве.
- 4. Геометрия возникла из практических нужд человека
- 5. АКСИОМЫ СТЕРЕОМЕТРИИЧерез любые две точки пространства проходит
- 6. ВОПРОС 1Сколько прямых проходит через две точки пространства?Ответ: Одна.
- 7. ВОПРОС 2Сколько плоскостей проходит через три точки
- 8. ВОПРОС 3Сколько общих точек могут иметь две плоскости?Ответ: Ни одной, или бесконечно много.
- 9. ВОПРОС 4Верно ли утверждение, что всякие: а)
- 10. ВОПРОС 5Верно ли, что если окружность имеет
- 11. ВОПРОС 6
- 12. ВОПРОС 7Ответ: Нет, прямая b не может
- 13. СЛЕДСТВИЯ ИЗ АКСИОМЕсли прямая имеет с плоскостью
- 14. Упражнение 1Четыре точки не принадлежат одной плоскости. Могут ли три из них принадлежать одной прямой?Ответ: Нет.
- 15. Упражнение 2Три вершины параллелограмма принадлежат некоторой плоскости.
- 16. Упражнение 3Две вершины и точка пересечения диагоналей
- 17. Упражнение 4Могут ли вершины замкнутой ломаной, состоящей из трёх звеньев, не принадлежать одной плоскости?Ответ: Нет.
- 18. Упражнение 5Могут ли вершины замкнутой ломаной, состоящей из четырёх звеньев, не принадлежать одной плоскости?Ответ: Да.
- 19. Упражнение 6Верно ли, что через любые две прямые проходит плоскость?Ответ: Нет.
- 20. Упражнение 7Прямые a, b, c попарно пересекаются. Верно ли, что они лежат в одной плоскости?Ответ: Нет.
- 21. Упражнение 8Верно ли, что любая прямая, пересекающая
- 22. Упражнение 9Прямые a и b пересекаются в
- 23. Упражнение 10Верно ли, что через любые две прямые проходит плоскость?Ответ: Нет.
- 24. Упражнение 11Верно ли, что через три пересекающиеся прямые проходит плоскость?Ответ: Нет.
- 25. Упражнение 12Сколько плоскостей можно провести через четыре точки?Ответ: Или одну, или ни одной.
- 26. Упражнение 13Сколько плоскостей можно провести через различные
- 27. Упражнение 14На сколько частей делят пространство три плоскости, имеющие одну общую точку?Ответ: 8.
- 28. Упражнение 15На какое наибольшее число частей могут
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Предмет стереометрия.
Аксиомы стереометрии.
Автор:
учитель математики
Комлякова Ксения Геннадьевна
ГБОУ Гимназия №105,
Слайд 5АКСИОМЫ СТЕРЕОМЕТРИИ
Через любые две точки пространства проходит единственная прямая
Через любые
три точки пространства, не принадлежащие одной прямой, проходит единственная плоскость
Если
две плоскости имеют общую точку, то они пересекаются по прямойСуществуют по крайней мере четыре точки, не принадлежащие одной плоскости
Слайд 7ВОПРОС 2
Сколько плоскостей проходит через три точки пространства?
Ответ: Одна, если
три точки не принадлежат одной прямой; бесконечно много в противном
случае.Слайд 9ВОПРОС 4
Верно ли утверждение, что всякие: а) три точки; б)
четыре точки пространства принадлежат одной плоскости?
Ответ: а) Да; б) нет.
Слайд 10ВОПРОС 5
Верно ли, что если окружность имеет с плоскостью две
общие точки, то окружность лежит в этой плоскости?
Ответ: Нет.
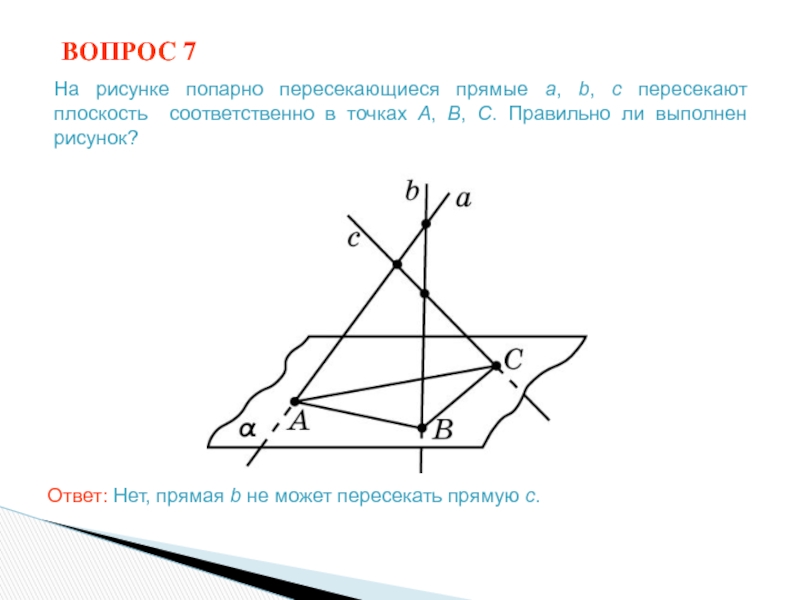
Слайд 12ВОПРОС 7
Ответ: Нет, прямая b не может пересекать прямую c.
На
рисунке попарно пересекающиеся прямые a, b, c пересекают плоскость соответственно
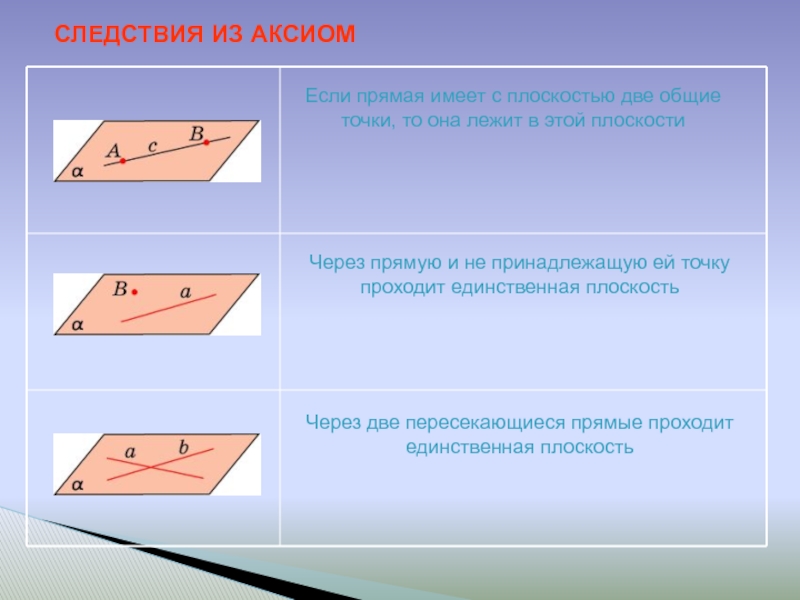
в точках A, B, C. Правильно ли выполнен рисунок?Слайд 13СЛЕДСТВИЯ ИЗ АКСИОМ
Если прямая имеет с плоскостью две общие точки,
то она лежит в этой плоскости
Через прямую и не принадлежащую
ей точку проходит единственная плоскостьЧерез две пересекающиеся прямые проходит единственная плоскость
Слайд 14Упражнение 1
Четыре точки не принадлежат одной плоскости. Могут ли три
из них принадлежать одной прямой?
Ответ: Нет.
Слайд 15Упражнение 2
Три вершины параллелограмма принадлежат некоторой плоскости. Верно ли утверждение
о том, что и четвёртая вершина этого параллелограмма принадлежит той
же плоскости?Ответ: Да.
Слайд 16Упражнение 3
Две вершины и точка пересечения диагоналей параллелограмма принадлежат одной
плоскости. Верно ли утверждение о том, что и две другие
вершины параллелограмма принадлежат этой плоскости?Ответ: Да.
Слайд 17Упражнение 4
Могут ли вершины замкнутой ломаной, состоящей из трёх звеньев,
не принадлежать одной плоскости?
Ответ: Нет.
Слайд 18Упражнение 5
Могут ли вершины замкнутой ломаной, состоящей из четырёх звеньев,
не принадлежать одной плоскости?
Ответ: Да.
Слайд 20Упражнение 7
Прямые a, b, c попарно пересекаются. Верно ли, что
они лежат в одной плоскости?
Ответ: Нет.
Слайд 21Упражнение 8
Верно ли, что любая прямая, пересекающая каждую из двух
данных пересекающихся прямых, лежит в плоскости этих прямых?
Ответ: Нет.
Слайд 22Упражнение 9
Прямые a и b пересекаются в точке C. Через
прямую a проходит плоскость , через прямую b
– плоскость , отличная от . Как проходит линия пересечения этих плоскостей?Ответ: Через точку C.
Слайд 25Упражнение 12
Сколько плоскостей можно провести через четыре точки?
Ответ: Или одну,
или ни одной.
Слайд 26Упражнение 13
Сколько плоскостей можно провести через различные тройки из пяти
точек, никакие четыре из которых не принадлежат одной плоскости?
Ответ: 10.
Слайд 27Упражнение 14
На сколько частей делят пространство три плоскости, имеющие одну
общую точку?
Ответ: 8.
Слайд 28Упражнение 15
На какое наибольшее число частей могут делить пространство; а)
одна плоскость; б) две плоскости; в) три плоскости; в) четыре
плоскости?Ответ: а) 2;
б) 4;
в) 8;
г) 15.