Свойства и признаки треугольников 7 класс

одной прямой, и тремя попарно соединенными отрезками.
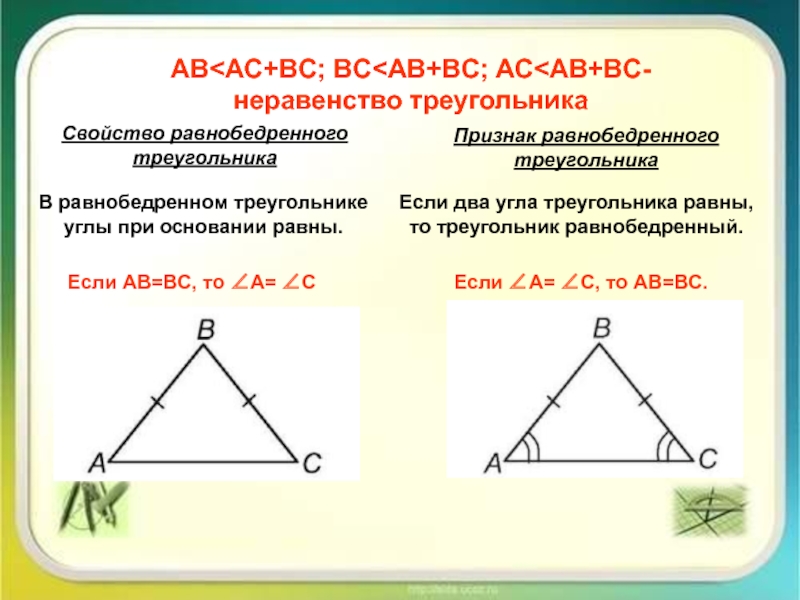
Точки называются вершинами треугольника.
Отрезки

называются сторонами треугольник.

Углы, образованные отрезками, выходящими из вершин треугольника, называется углами треугольника.

Обозначается: ABC или BCA или CAB.

ABC= MNK.
Два треугольника называются равными, если три стороны и три

угла одного треугольника соответственно равны трем сторонам углам другого треугольника.

углу между ними)
Если AB=KE, AC=KD;

∠A= ∠K, то ABC= KED

II признак

(по стороне и двум прилегающим углам)

Если AB=KE, ∠A= ∠K, ∠B=∠E, то ABC= KED

III признак

(по трем сторонам)

Если AB=KE, AC=KD BC=ED, то ABC=KED

Значит, для того чтобы утверждать, что два треугольника равны, достаточно знать равенство трех пар соответствующих элементов.

прямоугольным, если один угол прямой.
Треугольник называется тупоугольным, если один угол

тупой.

∠A<90˚, ∠B<90˚, ∠C<90˚

∠C<90˚

90 ˚ < ∠C<180 ˚

– равные стороны, называется боковыми сторонами; AC – называется основанием

треугольника.

Треугольник называется равносторонним, если все стороны равны.

MN=NK-MK

треугольника – угол, смежный с каким-нибудь углом данного треугольника.

∠BCD – внешний угол ABC при вершине C.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
∠BCD= ∠A+ ∠B
В треугольнике против большей стороны лежит большой угол, и обратно, против большего угла лежит большая сторона.
Каждая сторона треугольника меньше суммы двух других сторон.

при основании равны.
Если AB=BC, то ∠A= ∠C
Признак равнобедренного треугольника
Если два

угла треугольника равны, то треугольник равнобедренный.

Если ∠A= ∠C, то AB=BC.

против угла в 30°, равен половине гипотенузы.
Если ∠A=30°, то BC=1/2AB.
Если

∠B=30°, то AC=1/2AB.

Если катет равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°
Если AC=1/2AB, то ∠B=30°.
Если BC=1/2AB, то ∠A=30°.

катету и острому углу:
Если AC=MK, ∠B= ∠N,
то ABC= MNK.
3.По

гипотенузе и острому углу:
Если AB=MN, ∠A= ∠M,
то ABC=MNK

4.По катету и гипотенузе:
Если AC=MK, AB=MN,
То ABC=MNK

Значит, для того чтобы утверждать, что два прямоугольного треугольника равны, достаточно знать равенство двух пар соответствующих элементов.

углом.
AM – перпендикуляр к прямой j, AH ┴ j
Медианна треугольника

- отрезок, соединяющий вершину треугольника с серединой противоположной стороны треугольника.
BM- медиана, AM=MC

Биссектрисой треугольника- называется отрезок биссектрисы угла, соединяющий вершину треугольника с точкой на противоположной стороны треугольника.
AE- биссектриса, ∠BAE=∠CAE.

противоположную сторону треугольника
BH ┴ AC, AH1 ┴ BC1, BH и

AH1 – высоты.