Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Начальные геометрические сведения 7 класс
Содержание
- 1. Начальные геометрические сведения 7 класс
- 2. I.Точки, прямые, отрезки.1. Взаимное расположение точек и
- 3. 2.Свойства прямой: - какова ни
- 4. 3. Взаимное расположение прямых: две прямые либо
- 5. 4. Взаимное расположение точек на прямой.Точка С лежит между точками А и В.
- 6. 5. Отрезок. Часть прямой,
- 7. Упражнения.1. Назовите точки принадлежащие прямой а и
- 8. II. Провешивание прямой на местности.«Провешивание» от слова
- 9. III. Луч. Лучом называется часть прямой, состоящая из
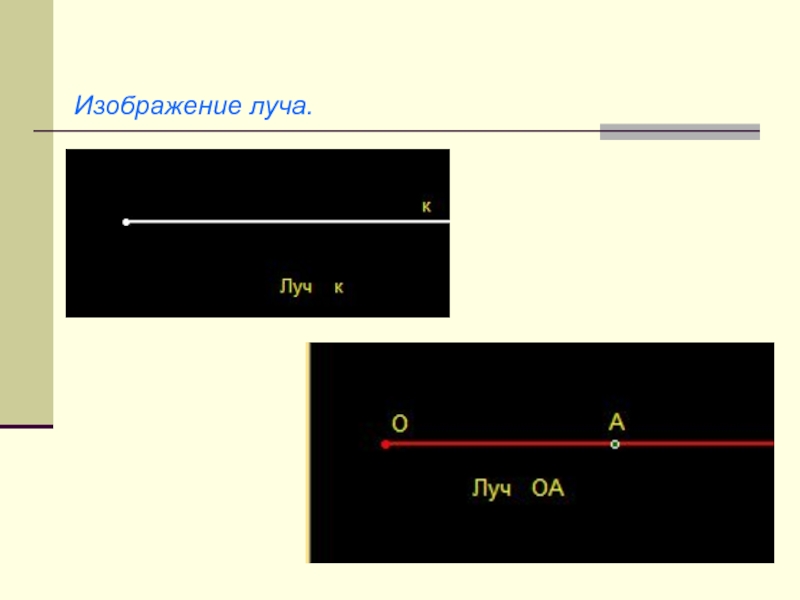
- 10. Изображение луча.
- 11. IV. Угол. Угол – это геометрическая фигура, которая
- 12. V. Равенство геометрических фигур.Две геометрические фигуры называют равными, если их можно совместить наложением.
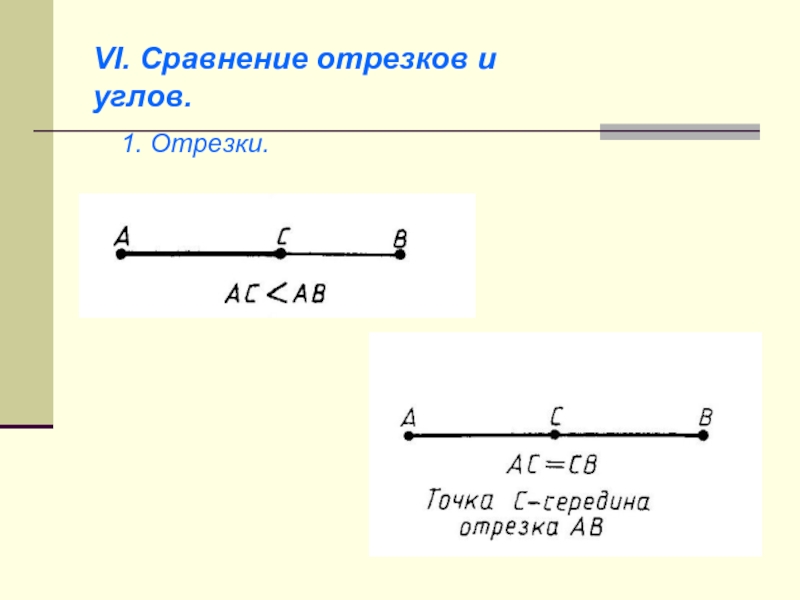
- 13. VI. Сравнение отрезков и углов. 1. Отрезки.
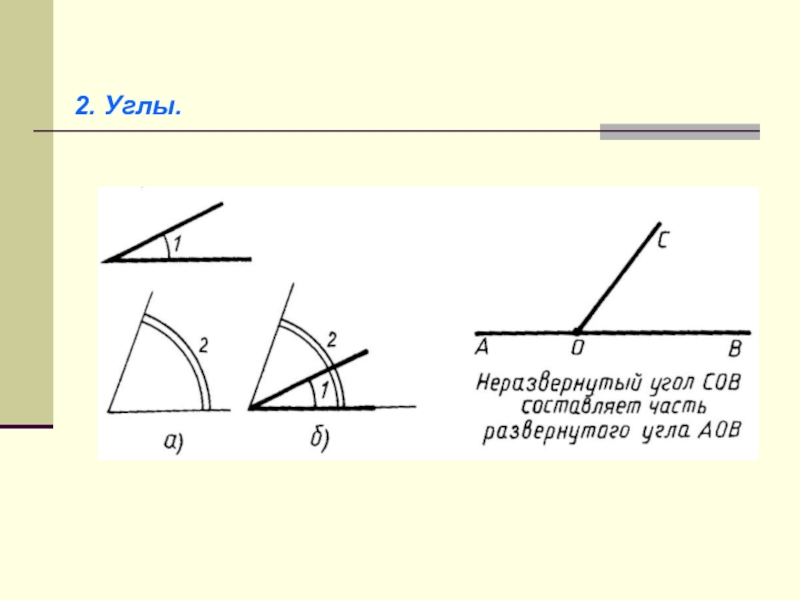
- 14. 2. Углы.
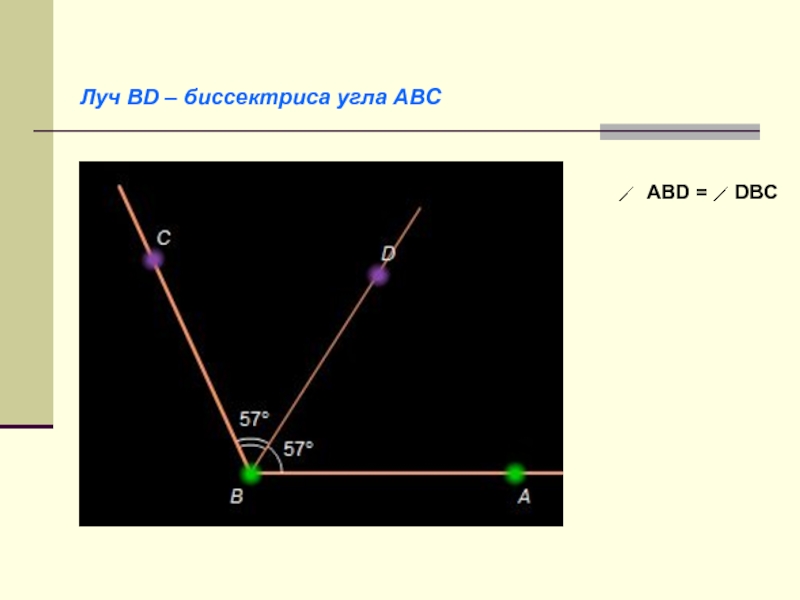
- 15. Луч ВD – биссектриса угла АВС АВD = DВС
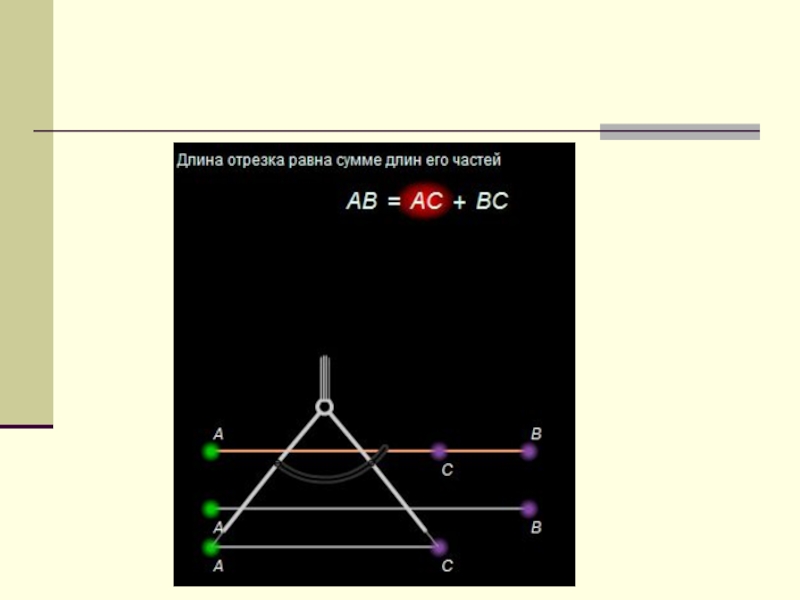
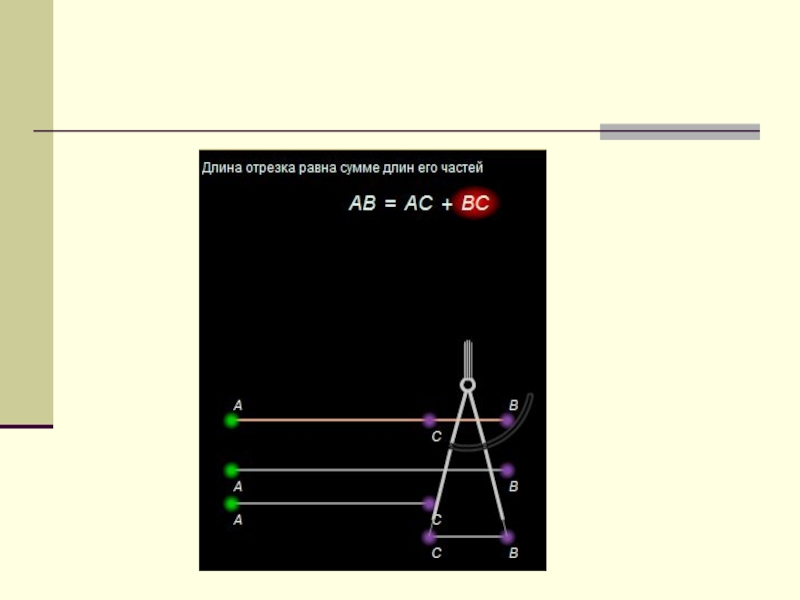
- 16. VII. Длина отрезка Каждый отрезок имеет определённую длину,
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Точка С – середина отрезка АВ, точка
- 21. Решение: 1. АС = СВ (по условию),
- 22. VIII. Единицы измерения.
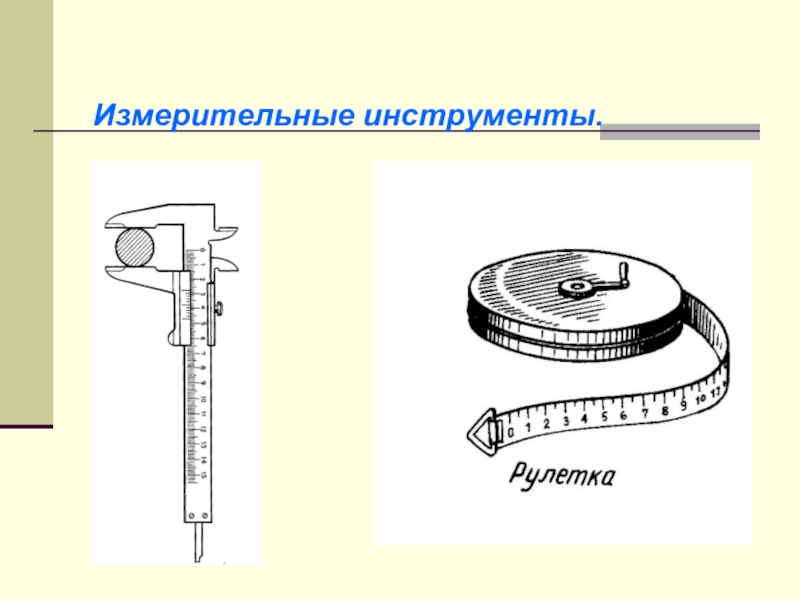
- 23. Измерительные инструменты.
- 24. IX. Градусная мера угла. Градусной мерой угла называется
- 25. Упражнения.Дано: АВD = 73 ,
- 26. Задача. Угол АВС равен 100 . Между его
- 27. Решение:1. Пусть угол АВD равен x градусов
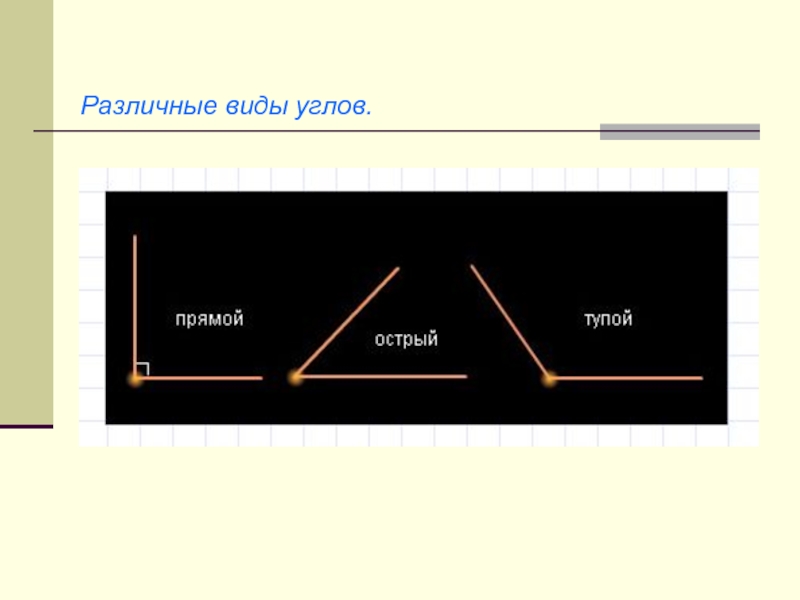
- 28. Различные виды углов.
- 29. X. Смежные и вертикальные углы.1. Смежные углы. Два
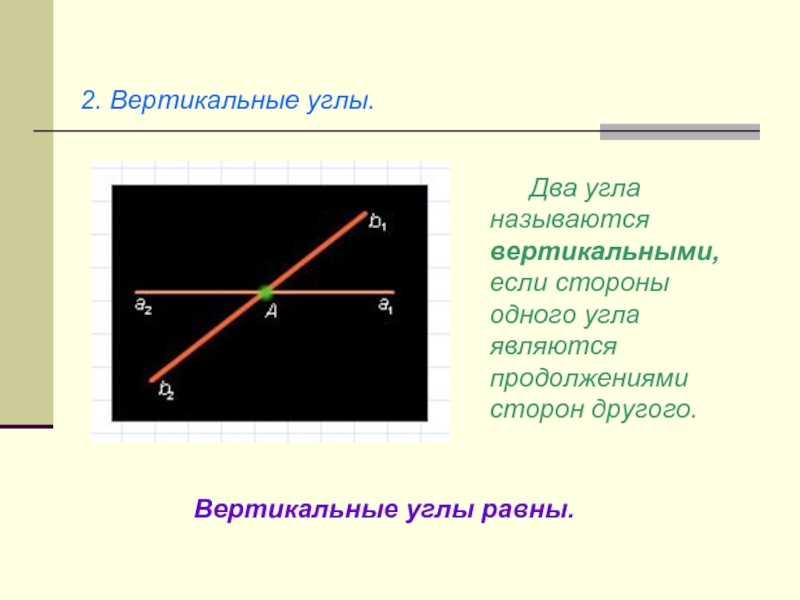
- 30. 2. Вертикальные углы. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.Вертикальные углы равны.
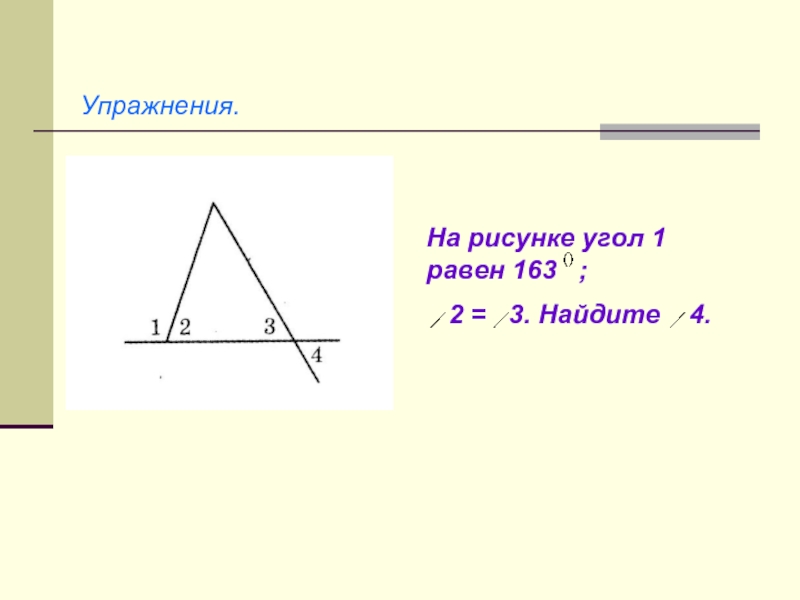
- 31. Упражнения.На рисунке угол 1 равен 163 ; 2 = 3. Найдите 4.
- 32. Скачать презентанцию
I.Точки, прямые, отрезки.1. Взаимное расположение точек и прямых.«точка А лежит на прямой а»: А а«точка В не лежит на прямой а»: В а
Слайды и текст этой презентации
Слайд 2I.Точки, прямые, отрезки.
1. Взаимное расположение точек и прямых.
«точка А лежит
на прямой а»: А а
не лежит на прямой а»: В а
Слайд 32.Свойства прямой:
- какова ни была прямая, существуют
точки принадлежащие этой прямой, и точки, не принадлежащие ей;
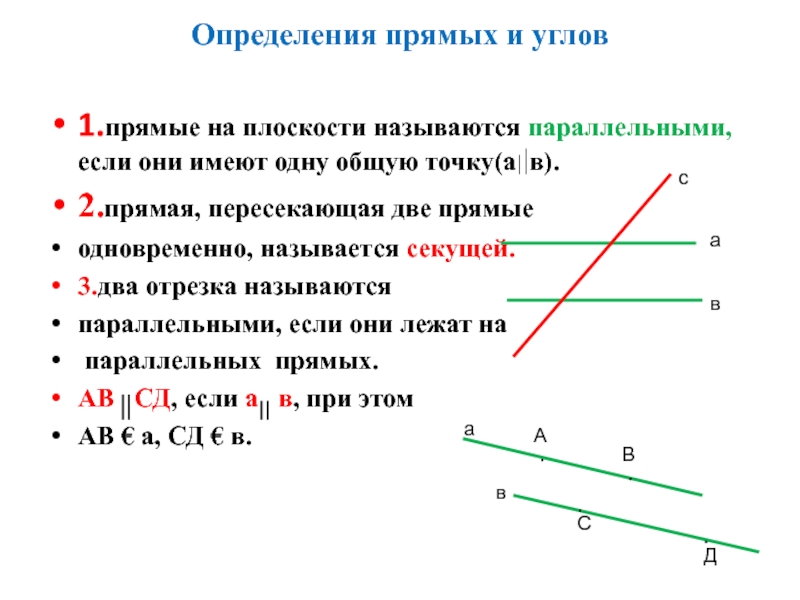
- через любые две точки можно провести прямую и притом только одну.
Слайд 43. Взаимное расположение прямых:
две прямые либо имеют только одну
общую точку, либо не имеют общих точек;
если две прямые
имеют общую точку, то говорят, что они пересекаются (а ∩ b = О).
Слайд 65. Отрезок.
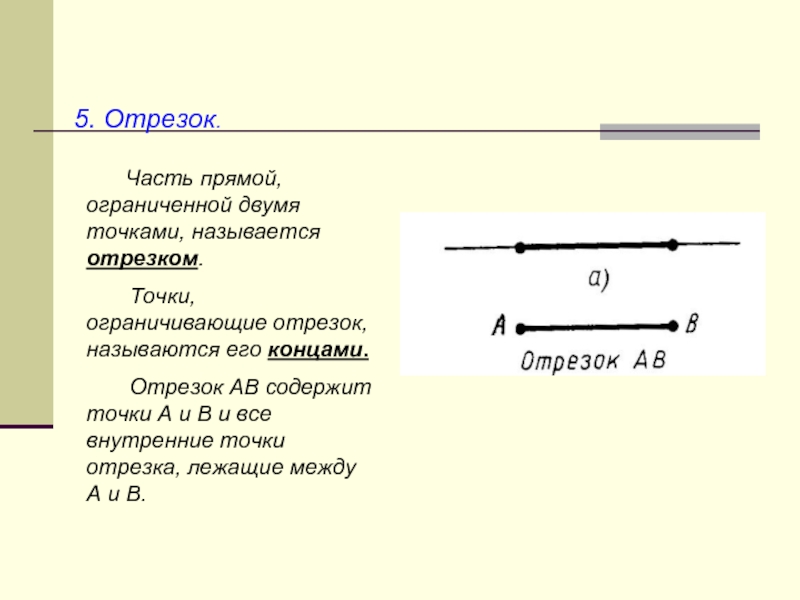
Часть прямой, ограниченной двумя точками,
называется отрезком.
Точки, ограничивающие отрезок, называются его
концами.Отрезок АВ содержит точки А и В и все внутренние точки отрезка, лежащие между А и В.
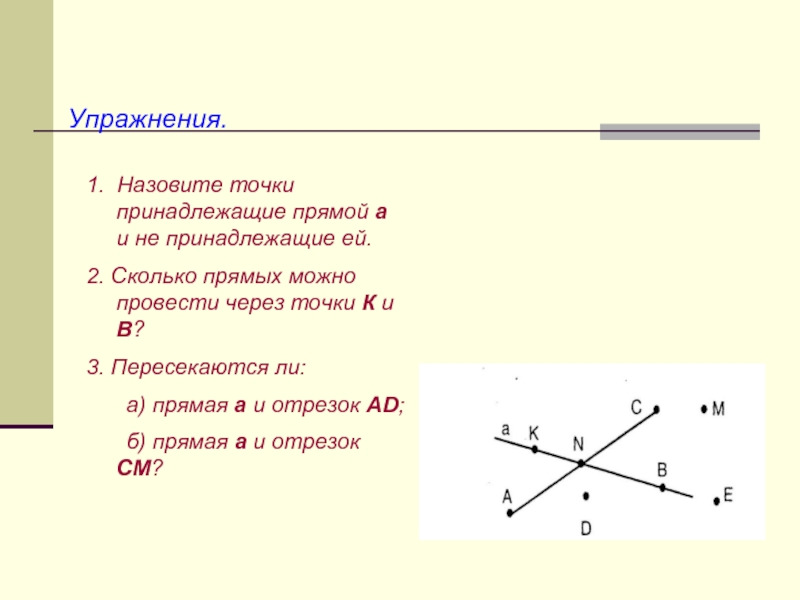
Слайд 7Упражнения.
1. Назовите точки принадлежащие прямой а и не принадлежащие ей.
2.
Сколько прямых можно провести через точки К и В?
3. Пересекаются
ли:а) прямая а и отрезок АD;
б) прямая а и отрезок СМ?
Слайд 8II. Провешивание прямой на местности.
«Провешивание» от слова «веха». Широко
используется на практике, например при рубке лесных просек, при прокладывании
трассы шоссейной или железной дороги, линии высоковольтных передач и т. д.
Слайд 9III. Луч.
Лучом называется часть прямой, состоящая из всех точек, которые
лежат по одну сторону от фиксированной точки прямой, и самой
этой точки, называемой началом луча.Разные лучи одной прямой с общим началом называются дополнительными.
Слайд 11IV. Угол.
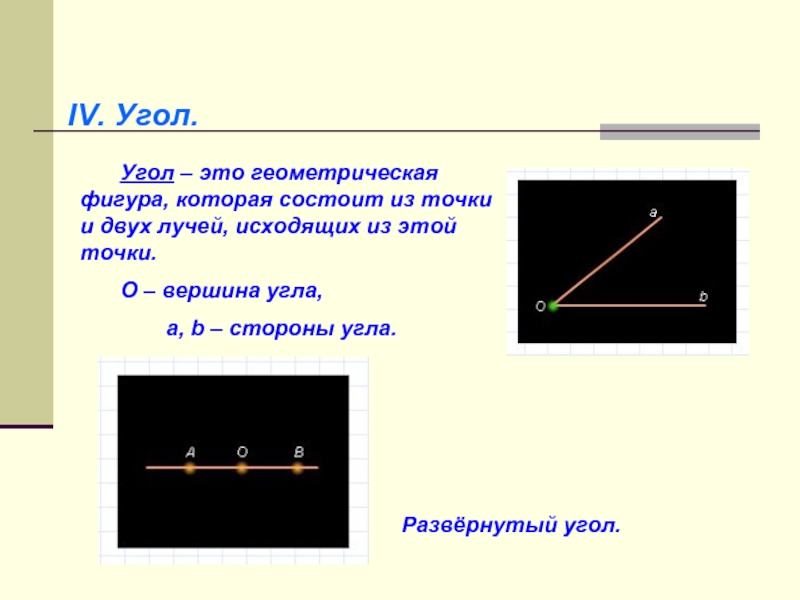
Угол – это геометрическая фигура, которая состоит из точки
и двух лучей, исходящих из этой точки.
О – вершина угла,
а, b – стороны угла.Развёрнутый угол.
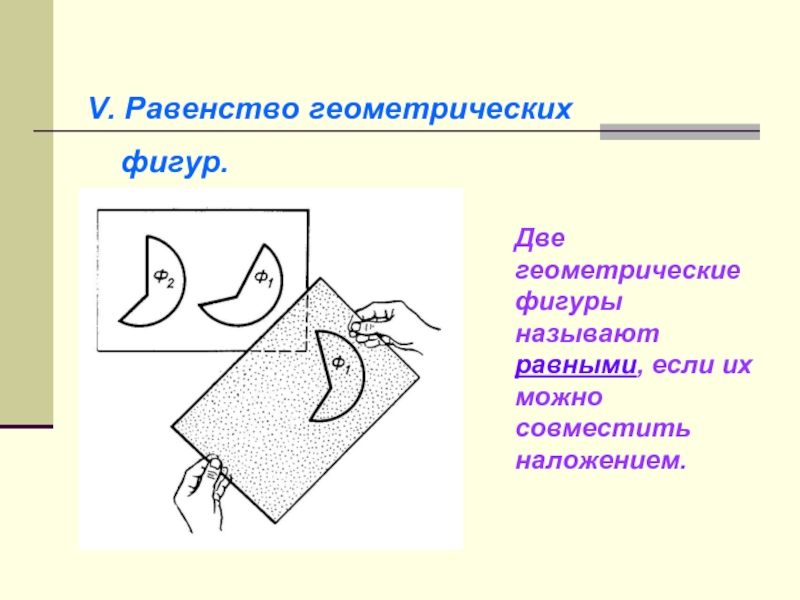
Слайд 12V. Равенство геометрических
фигур.
Две геометрические фигуры называют равными,
если их можно совместить наложением.
Слайд 16VII. Длина отрезка
Каждый отрезок имеет определённую длину, большую нуля.
Длина отрезка
АВ называется расстоянием между двумя точками А и В.
Слайд 20 Точка С – середина отрезка АВ, точка D – середина
отрезка АС, ВD=15,3 см. Найдите длину отрезка АС и выразите
её в миллиметрах.Задача.
Дано: АВ – отрезок,
АС = СВ, АD = DС,
ВD = 15,3 см
----------------------------------------
Найти: АС.
Слайд 21Решение:
1. АС = СВ (по условию),
АД
= ДС (по условию),
значит АС = 2АД
и СВ = 2АД.2. АВ = АС + СВ = 4АД.
3. ДВ = АВ – АД
ДВ = 4АД – АД
ДВ = 3АД
15,3 = 3АД
АД = 15,3 : 3 = 5,1 (см)
4. АС = 2 · 5,1 = 10,2 (см)
Ответ: АС = 10,2 см = 102 мм.
Слайд 22VIII. Единицы измерения.
1. Стандартная единица
измерения.
2. Миллиметр, сантиметр, дециметр, километр.
3. Морская миля (1,852 км), световой
год.4. Аршин (0,7112 м), сажень (2,1336 м).
Слайд 24IX. Градусная мера угла.
Градусной мерой угла называется положительное число, которое
показывает, сколько раз градус и его части укладываются в данном
угле. Градус – угол, равный 1/180 части развёрнутого угла.
Равные углы имеют равные градусные меры.
Меньший угол имеет меньшую градусную меру.
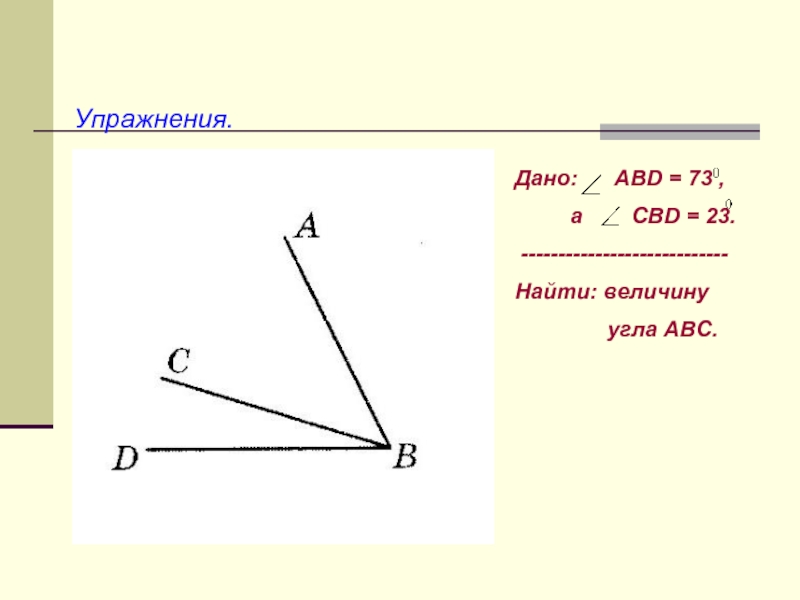
Слайд 25Упражнения.
Дано: АВD = 73 ,
а СВD = 23.
----------------------------
Найти: величину
угла АВС.
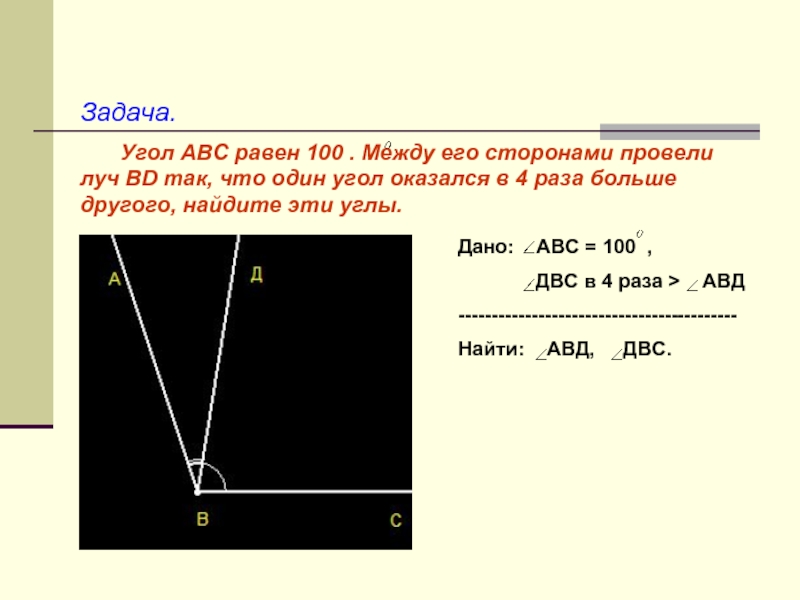
Слайд 26Задача.
Угол АВС равен 100 . Между его сторонами провели луч
ВD так, что один угол оказался в 4 раза больше
другого, найдите эти углы.Дано: АВС = 100 ,
ДВС в 4 раза > АВД
------------------------------------------
Найти: АВД, ДВС.
Слайд 27Решение:
1. Пусть угол АВD равен x градусов
тогда
угол DВС равен 4х градусов.
2. Составим уравнение:
х +
4х = 1005х = 100
х = 20
3. 20 · 4 = 80
Ответ: АВD = 20 , DВС = 80 .
Слайд 29X. Смежные и вертикальные углы.
1. Смежные углы.
Два угла, у которых
одна сторона общая, а две другие являются продолжениями одна другой,
называются смежными.Сумма смежных углов равна 180 .
Слайд 302. Вертикальные углы.
Два угла называются вертикальными, если стороны одного угла
являются продолжениями сторон другого.
Вертикальные углы равны.
Теги
