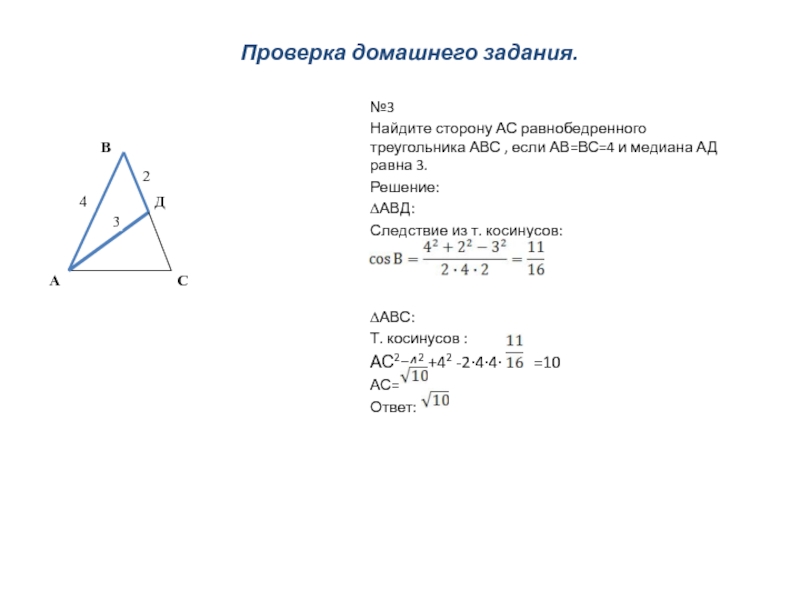
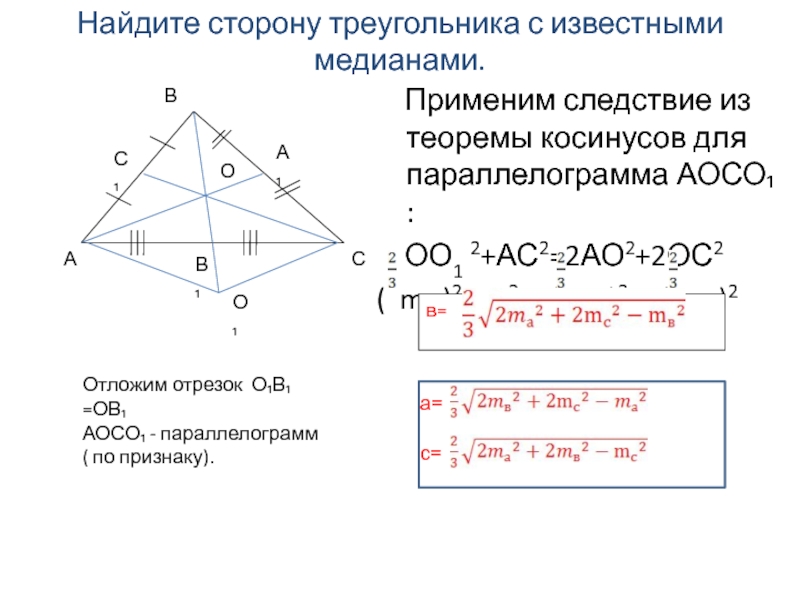
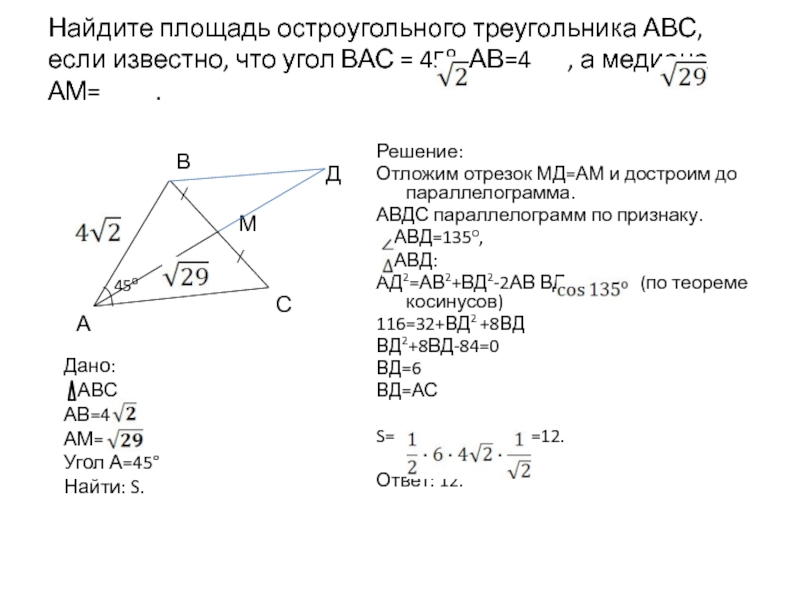
угол лежит против стороны, равной 17, то по следствию из
теоремы косинусов:Треугольник прямоугольный.
Ответ: треугольник прямоугольный.
№ 2
Найдите сторону АВ в треугольнике АВС, если АС=0,6, ВС= , ∠С=150о.
Решение :
По теореме косинусов:
АВ2=0,62 + ( )2 - 2∙ 0, 6∙ ∙ ,
АВ2=0,9975
АВ=
Ответ :