Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Использование метода координат в пространстве для решения заданий С2 на ЕГЭ
Содержание
- 1. Использование метода координат в пространстве для решения заданий С2 на ЕГЭ
- 2. Исследование выполнил: ученик 11а класса сш№177
- 3. Координатный метод решения заключается во введении (привязке
- 4. Алгоритм применения метода координат к решению геометрических
- 5. В задании С2 чаще всего требуется найти:
- 6. Углом между скрещивающимися прямыми называется угол между
- 7. Задача на нахождение угла между скрещивающимися прямыми.Сторона
- 8. РешениехС уА
- 9. Углом между плоскостью и
- 10. Задача на нахождение угла между прямой и
- 11. РешениеДля решения этой задачи необходимо воспользоваться уравнением
- 12. Длину вектора легко найти геометрически: Но его
- 13. Двугранный угол, образованный полуплоскостями измеряется величиной его
- 14. Задача на нахождение угла между двумя плоскостями. В
- 15. Решение.Введём прямоугольную систему координат. Тогда А(0;0;0), С(1;1;0),
- 16. Расстояние между точками А и В можно
- 17. Задача на нахождение расстояния между двумя точками. В
- 18. Решение. Поместим пирамиду в прямоугольную систему координат, как
- 19. Задача. В единичном кубе АВСDA1В1С1D1 точки Е и
- 20. Решение. Введём декартову систему координат. E(1;0;0,5), K(0,5;1,0), В1(0;0;1),
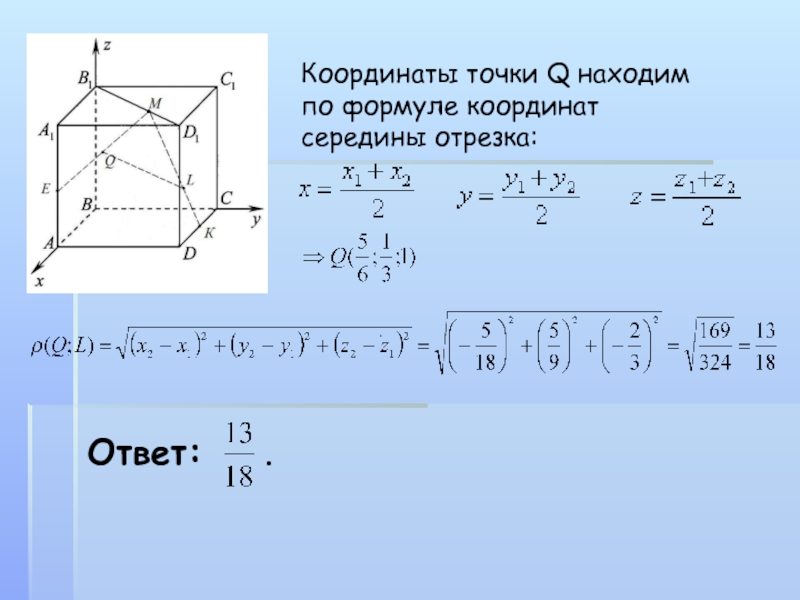
- 21. Координаты точки Q находим по формуле координат середины отрезка:. Ответ: .
- 22. Расстояние от точки до плоскости, не содержащей
- 23. Задача на нахождение расстояния от точки до
- 24. Решение.Составим уравнение плоскости А1BC1 и найдём расстояние
- 25. Задача.
- 26. Решение.Выберем систему координат как показано на рисунке
- 27. Как вы видите, все те соотношения, которые
- 28. Благодарим за внимание!
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Исследование выполнил:
ученик 11а класса сш№177
САБИРОВ ИЛЬДАР
Научный руководитель: учитель
математики высшей категории Хабибуллина А.Я
Слайд 3 Координатный метод решения заключается во введении (привязке к исследуемым фигурам)
декартовой системы координат, а затем – исчислении образующихся векторов (их
длин и углов между ними).Мы уже хорошо знакомы с векторами, координатами и их свойствами. Цель моей работы: научиться применять знания для решения задач стереометрии (С2).
Слайд 4 Алгоритм применения метода координат к решению геометрических задач сводится к
следующему:
Выбираем в пространстве систему координат из соображений удобства выражения координат
и наглядности изображения.Находим координаты необходимых для нас точек.
Решаем задачу, используя основные задачи метода координат.
Переходим от аналитических соотношений к геометрическим.
Слайд 5 В задании С2 чаще всего требуется найти:
угол между двумя
скрещивающимися прямыми,
угол между прямой и плоскостью,
угол между двумя
плоскостями,расстояние между двумя скрещивающимися прямыми,
расстояние от точки до прямой,
расстояние от точки до плоскости.
Слайд 6
Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными
им и проходящими через произвольную точку.
При нахождении угла между
прямыми используют формулу или в координатной форме
для нахождения угла φ между прямыми m и l, если векторы и параллельны соотвественно этим прямым; в частности, для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы или .
Слайд 7Задача на нахождение угла между скрещивающимися прямыми.
Сторона основания правильной четырехугольной
призмы ABCDA1B1C1D1 равна 2, высота — 4. Точка E —
середина отрезка CD, точка F — середина отрезка AD. Найдите угол между прямыми CF и B1E.Слайд 8Решение
х
С у
А F
D
E
B
z
B1
C1A1 D1
Поместим параллелепипед в прямоугольную систему координат, как показано на рисунке, и найдём искомый угол как угол между векторами. Выпишем координаты точек B1, E, C, F в этой системе координат: B1 (0; 0; 4), E(1; 2; 0), C (0; 2; 0), F (2; 1; 0).
Тогда {2; -1; 0}, {1; 2; -4}. Найдём угол между этими векторами по формуле:
То есть искомый угол α=90˚.
Ответ: 90˚.
Слайд 9 Углом между плоскостью и не перпендикулярной ей
прямой называется угол между этой прямой и её проекцией на
данную плоскость.Угол между прямой l и плоскостью α можно вычислить:
1) по формуле ;
2) по формуле
или в координатах
, где
- вектор нормали к плоскости α,
- направляющий векор прямой l
Слайд 10Задача на нахождение угла между прямой и плоскостью.
В прямоугольном параллелепипеде
ABCDA1B1C1D1 рёбра АВ и АА1 равны 1, а ребро АD=2.
Точка Е – середина ребра В1С1. Найдите угол между прямой ВЕ и плоскостью АВ1С.Слайд 11Решение
Для решения этой задачи необходимо воспользоваться уравнением плоскости, имеющим общий
вид
ах+bу+cz+d=0, где a, b и c – координаты нормали
к плоскости.Чтобы составить это уравнение, необходимо определить координаты трёх точек, лежащих в данной плоскости: А(1; 0; 0), В1(0;0;1), С(0;2;0).
Решая систему
находим коэффициенты а, b и с уравнения ах+bу+cz+d=0: а=-d, b= , c=-d. Таким образом, уравнение примет вид
или, после упрощения, 2х+у+2z-2=0. Значит нормаль n к этой плоскости имеет координаты .
Слайд 12Длину вектора легко найти геометрически:
Но его координаты нам всё
равно необходимы. Из простых вычислений находим, что
.Найдем угол между вектором и нормалью к плоскости по формуле скалярного произведения векторов:
Ответ: 45˚
Слайд 13Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого
при пересечении двугранного угла плоскостью, перпендикулярной его ребру.
Угол между двумя
пересекающимися плоскостями можно вычислить:по формуле
как угол между нормалями по формуле
или в координатной форме
где - вектор нормали плоскости А1х+В1у+С1z+D1=0,
- вектор нормали плоскости A2x+B2y+C2z+D2=0.
Слайд 14Задача на нахождение угла между двумя плоскостями.
В единичном кубе АВСDA1В1С1D1
найдите угол между плоскостями АD1 Е и D1FC, где точки
Е и F-середины ребер А1В1 и В1С1.Слайд 15Решение.
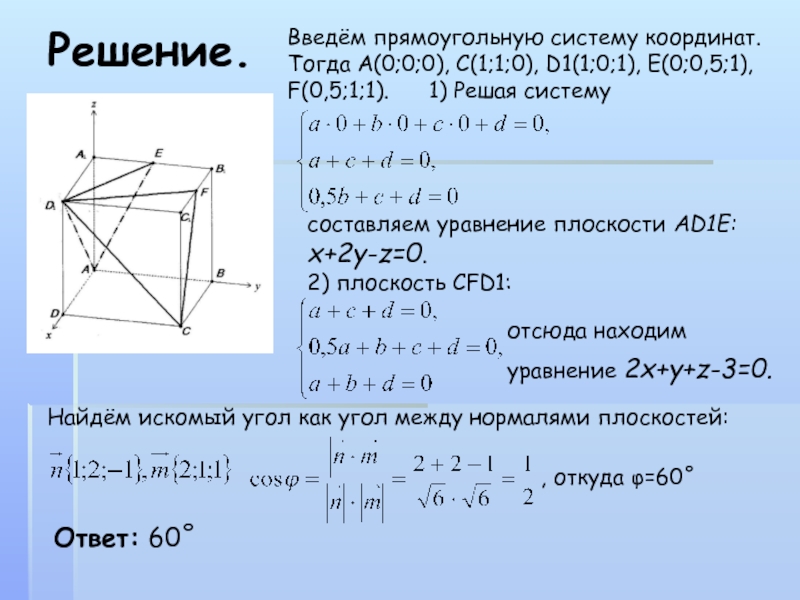
Введём прямоугольную систему координат. Тогда А(0;0;0), С(1;1;0), D1(1;0;1), E(0;0,5;1), F(0,5;1;1).
1) Решая систему
составляем уравнение плоскости АD1E: x+2y-z=0.
2)
плоскость CFD1:отсюда находим уравнение 2x+y+z-3=0.
Найдём искомый угол как угол между нормалями плоскостей:
, откуда φ=60˚
Ответ: 60˚
Слайд 16 Расстояние между точками А и В можно вычислить:
1) по формуле
,
где A(x1; y1; z1), B(x2; y2; z2);
2) по формуле .
Слайд 17 Задача на нахождение расстояния между двумя точками.
В основании пирамиды SABCD
лежит ромб со стороной 2 и острым углом в 60˚.
Боковое ребро SA перпендикулярно основанию пирамиды и равно 4. Найдите расстояние от середины Н ребра SD и серединой М ребра ВС.Слайд 18Решение.
Поместим пирамиду в прямоугольную систему координат, как показано на рисунке.
Найдём координаты точки Н как координаты середины отрезка SD: S(0;
0; 4), D(0; 2; 0).Чтобы найти координаты точек В и С, найдём координаты их проекций на оси. АВх=ACx=2·cos30˚= ,
ABy=ACу–2=2·cos60˚=1.
Отсюда В( ;1;0), С( ;3;0). Тогда координаты точки М равняются:
Теперь находим расстояние между точками, заданными своими координатами:
Ответ:
Слайд 19Задача.
В единичном кубе АВСDA1В1С1D1 точки Е и К – середины
ребер АА1 и СD соответственно, а точка М расположена на
диагонали В1D1 так, что В1М = 2МD1. Найдите расстояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МК такая, что ML=2LK.Слайд 20Решение.
Введём декартову систему координат. E(1;0;0,5), K(0,5;1,0), В1(0;0;1), D1(1;1;1). Чтобы вычислить
координаты т.М, воспользуемся формулой для нахождения координат точки, которая делит
отрезок B1D1 в отношении λ=2:1:Аналогично находим координаты точки L:
Слайд 22 Расстояние от точки до плоскости, не содержащей эту точку, есть
длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
Расстояние от
точки М до плоскости αвычисляется по формуле , где ρ=ρ(М;α), ρ1=ρ(М1;α), ОМ=r, ОМ1=r1, ММ1∩α=0; в частности, ρ=ρ1, если r=r1: прямая m, проходящая через точку М, пересекает плоскость α в точке О, а точка М1 лежит на прямой m;
вычисляется по формуле ,
где М(х0;у0;z0), плоскость α задана уравнением ax+by+cz+d=0;
Слайд 23 Задача на нахождение расстояния от точки до плоскости.
В кубе АВСDA1B1C1D1
проведена диагональ B1D. В каком отношении, считая от вершины B1,
плоскость А1BC1 делит диагональ B1D?Слайд 24Решение.
Составим уравнение плоскости А1BC1 и найдём расстояние от этой плоскости
до каждой из точек B1 и D. Пусть l –
ребро куба. В(0;0;0), А1(l;0;l), С1(0;l;l).Решив систему
определяем, что уравнение плоскости имеет вид: x+y–z=0 → а=1, b=1, c= –1. B1(0;0;1), D(1;1;0).
Теперь найдём расстояние от каждой точки до плоскости по формуле
Ответ: 2:1.
Слайд 25 Задача. Основание прямой призмы АВСА1В1С1 –
равнобедренный треугольник АВС, основание АС и высота ВD которого равны
4. Боковое ребро равно 2. Через середину К отрезка В1С проведена плоскость, перпендикулярная к этому отрезку. Найдите расстояние от вершины А до этой плоскости.Слайд 26Решение.
Выберем систему координат как показано на рисунке и выпишем координаты
вершин данной призмы и точки К в этой системе координат:
А(0;–2;0), В(0;0;0), С(0;2;0), В1(4;0;2), К(2;1;1). Тогда . Этот вектор перпендикулярен плоскости, значит, он является его нормалью. К тому же плоскость проходит через точку К. То есть уравнение плоскости имеет вид –2(x–2)+2(у–1)–2(z–1)=0 или, после упрощения, 2x–y+z-4=0.Теперь находим расстояние от т.А(0;-2;0) до плоскости:
Ответ: .