Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Медианы, биссектрисы и высоты треугольника. Свойства равнобедренного треугольника 7 класс
Содержание
- 1. Медианы, биссектрисы и высоты треугольника. Свойства равнобедренного треугольника 7 класс
- 2. Медианы треугольника. Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок
- 3. Свойсва медиан треугольника 1. Медианы треугольника точкой
- 4. Биссектрисы треугольникаБиссектри́са (от лат. bi- «двойное», и sectio «разрезание») угла — луч с началом в вершине угла,
- 5. Свойства биссектрис треугольника1. Три биссектрисы треугольника пересекаются
- 6. Высоты треугольникаВысота треугольника — перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
- 7. Свойства высот треугольника1. В остроугольном треугольнике все
- 8. Задача 1Дано: ∆ABC углы А и В
- 9. Равнобедренный треугольник — это треугольник, в котором две стороны
- 10. 1 свойство: Углы, противолежащие равным сторонам равнобедренного
- 11. Задача №2Дано: в ∆ABC со сторонами АВ=3 см,
- 12. Спасибо за урок!
- 13. Скачать презентанцию
Медианы треугольника. Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.На рисунке АА₁ , ВВ₁ и СС₁ – медианы.
Слайды и текст этой презентации
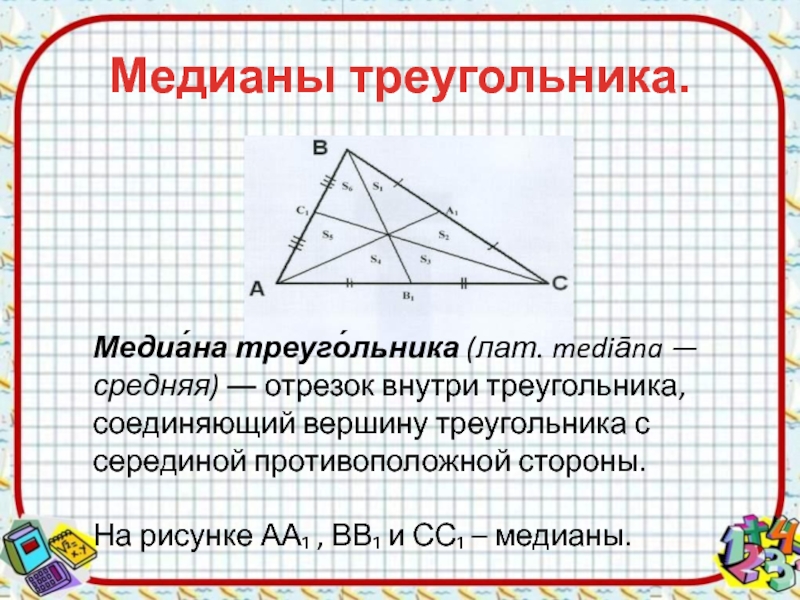
Слайд 2Медианы треугольника.
Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок внутри треугольника, соединяющий вершину
треугольника с серединой противоположной стороны.
СС₁ – медианы.
Слайд 3Свойсва медиан треугольника
1. Медианы треугольника точкой их пересечения делятся
в отношении 2:1 (считая от вершин треугольника).
2. Медиана делит треугольник
на два равновеликих треугольника. (Два треугольника равновелики, если их площади равны.)3. Три медианы треугольника делят
Слайд 4Биссектрисы треугольника
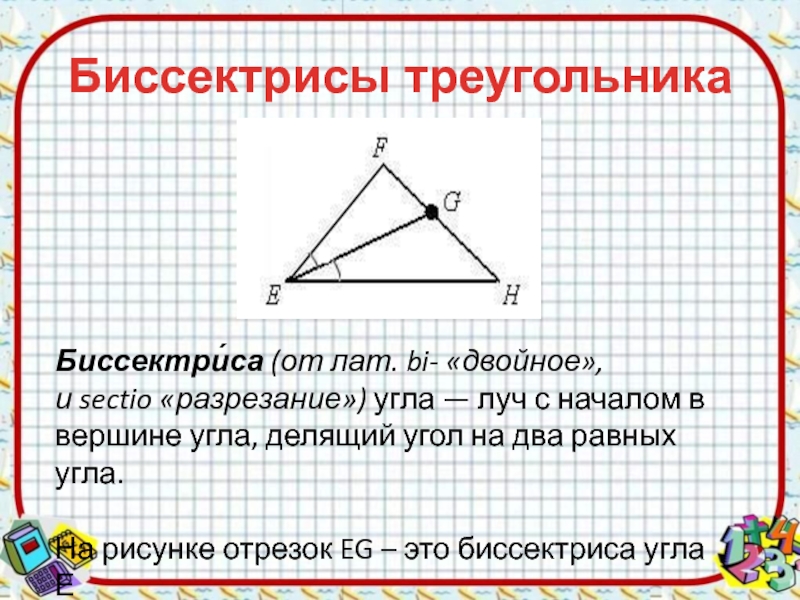
Биссектри́са (от лат. bi- «двойное», и sectio «разрезание») угла — луч с началом в вершине угла, делящий угол на
два равных угла.
На рисунке отрезок EG – это биссектриса угла
Е
Слайд 5Свойства биссектрис треугольника
1. Три биссектрисы треугольника пересекаются в одной точке.
2.
Биссектриса делит противоположную сторону на части, пропорциональные прилежащим к ней
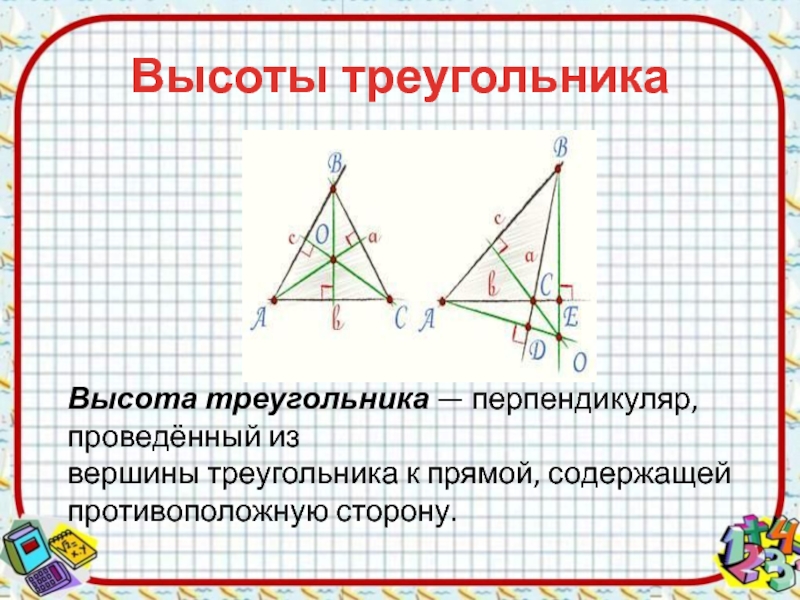
сторонам.
Слайд 6Высоты треугольника
Высота треугольника — перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Слайд 7Свойства высот треугольника
1. В остроугольном треугольнике все три высоты лежат
внутри треугольника.
2. В тупоугольном треугольнике две высоты пересекают продолжение сторон
и лежат вне треугольника; третья высота пересекает сторону треугольника.
Слайд 8Задача 1
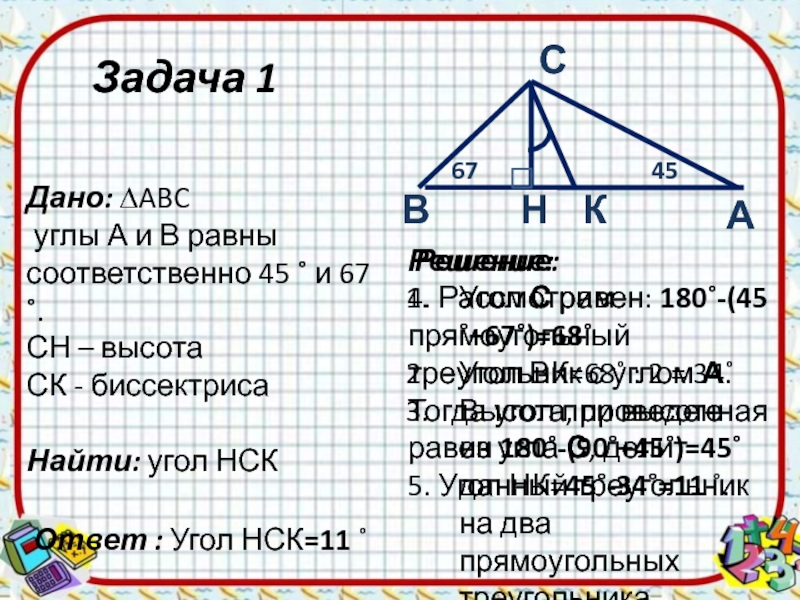
Дано: ∆ABC
углы А и В равны соответственно 45
˚ и 67 ˚.
СН – высота
СК - биссектриса
Найти: угол
НСКОтвет : Угол НСК=11 ˚
А
С
Н
В
Решение:
Угол С равен: 180˚-(45˚+67˚)=68˚
Угол ВК=68˚ : 2 = 34˚
Высота, проведенная из угла С, делит данный треугольник на два прямоугольных треугольника.
К
45
67
Решение:
4. Рассмотрим прямоугольный треугольник с углом А. Тогда угол при высоте равен 180˚-(90˚+45˚)=45˚
5. Угол НК=45˚-34˚=11 ˚.
Слайд 9Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой
по длине. Равные стороны называются боковыми, а последняя — основанием.
Свойства биссектрис
треугольника
Слайд 101 свойство: Углы, противолежащие равным сторонам равнобедренного треугольника, равны между
собой. Также равны биссектрисы, медианы и высоты, проведённые из этих углов.
2 свойство: В
равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.Свойства биссектрис треугольника
Слайд 11Задача №2
Дано: в ∆ABC со сторонами АВ=3 см, ВС=3см и АС=2см
проведена биссектриса ВН.
Найти: длины отрезков АН и НС
Ответ
: АН=1 смНС=1см
Решение:
Т. к. АВ=ВС, то ∆АВС – равнобедренный, следовательно АН – биссектриса, медиана и высота
АН=АС= ½ АС
АН=АС= 2 : 2 = 1
