Сферические координаты

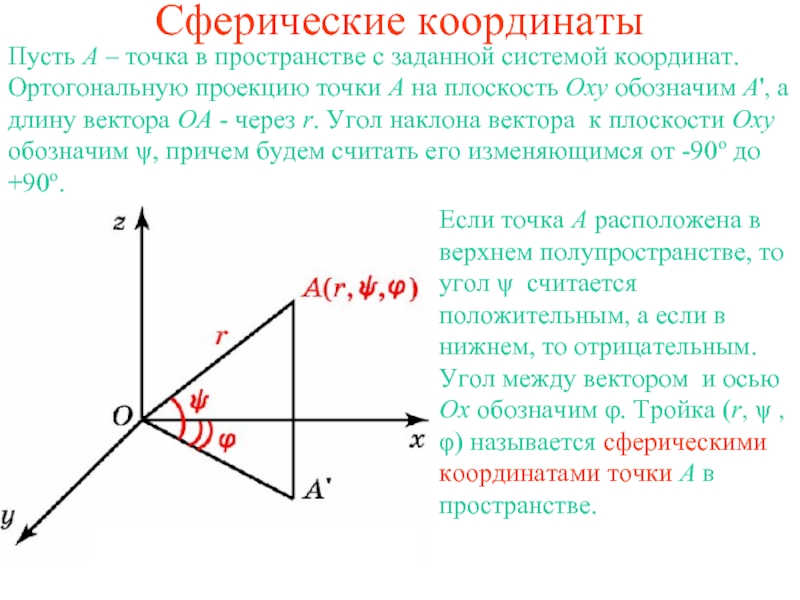
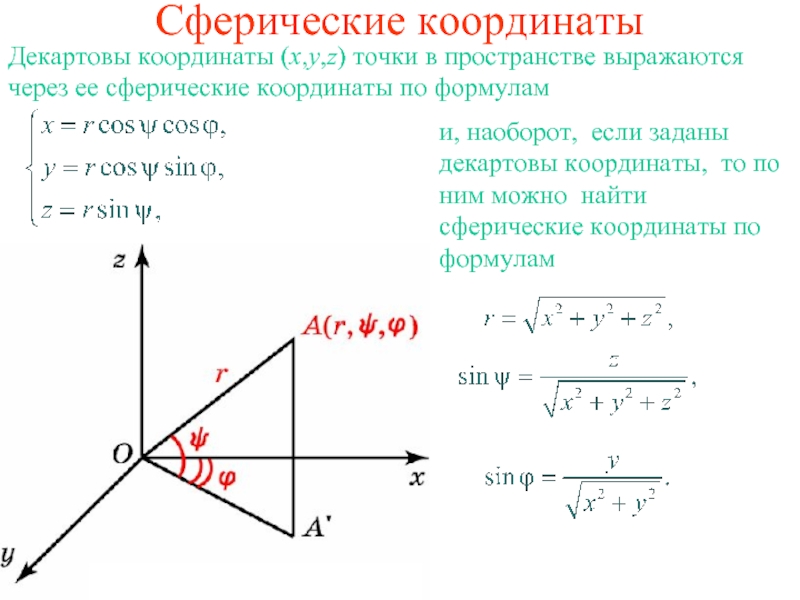
координат. Ортогональную проекцию точки A на плоскость Oxy обозначим A',

Если точка A расположена в верхнем полупространстве, то угол ψ считается положительным, а если в нижнем, то отрицательным. Угол между вектором и осью Ox обозначим φ. Тройка (r, ψ , φ) называется сферическими координатами точки A в пространстве.

сферические координаты по формулам
и, наоборот, если заданы декартовы координаты, то

которая называется параллелью. Точки, имеющие одинаковый угол φ, образуют полуокружность,

Дуга большой окружности, соединяющая две точки сферы, является кратчайшим путем на сфере между этими двумя точками. Такой путь называют ортодромией, что в переводе с греческого означает "прямой бег".

Кривая, образующая равные углы с разными меридианами, называется локсодромия, что в переводе с греческого означает "косой бег".

точек пространства, заданных своими сферическими координатами: (1,45°,120°), (2,-30°,-90°), (1,90°, 60°).

точек пространства, заданных своими декартовыми координатами: A(1,1,1), B(-1,0,1), C(0,0,2).

куба, задаваемого в декартовых координатах системой неравенств

координаты (r, ψ, ϕ). Найдите сферические координаты точки, симметричной данной,

Ответ: а) (r, -ψ, ϕ), (r, ψ, 180о-ϕ), (r, ψ, -ϕ);

б) (r, -ψ, -ϕ), (r, -ψ, 180о-ϕ), (r, ψ, 180о+ϕ);

в) (r, -ψ, 180о+ϕ).

пространства, сферические координаты которых удовлетворяют условиям: а) r постоянно; б)

Ответ: а) Сфера;

б) коническая поверхность;

в) полуплоскость.

задается неравенствами: а) 0 ≤ r ≤ 1, 0 ≤

Ответ: а) Полушар;

б) полушар;

в) четверть шара.

заданными своими сферическими координатами: A( ,0°,45°), B(2,60°,0°).




Ответ: 2.

острый угол с меридианами, при ее продолжении в обе стороны?




Ответ:

сферических координатах
Ответ: r = 1.

ортодромии, соединяющих точки A1(R, 45°, 0°), A2(R, 45°, 180°) на