Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движение
Содержание
- 1. Движение
- 2. Преобразование фигур Если каждую точку
- 3. ДвижениеПреобразованием одной фигуры F в другую F
- 4. Свойства движенияДва движения, выполненные последовательно, дают снова
- 5. Свойства движения2. Точки, лежащие на прямой, при
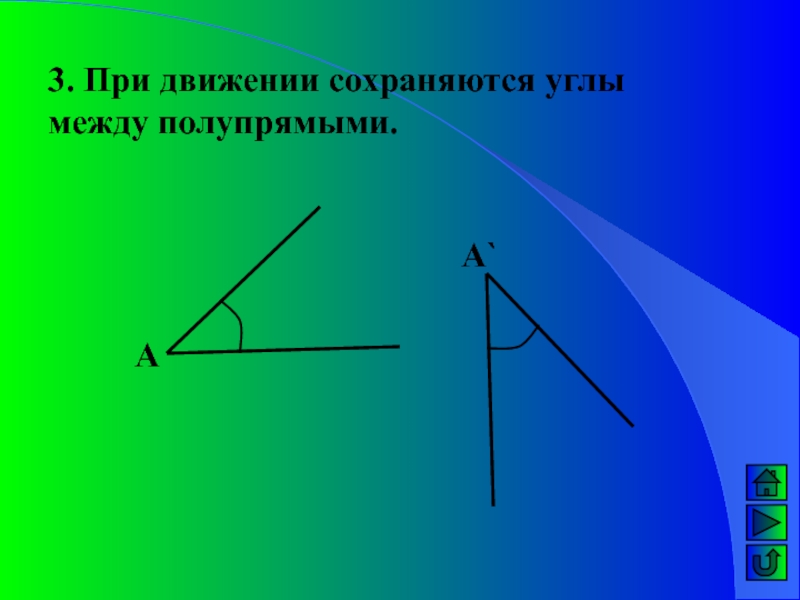
- 6. 3. При движении сохраняются углы между полупрямыми.АА`
- 7. Симметрия относительно точкиПусть О – фиксированная точкаи
- 8. Симметрия фигуры относительно точкиПреобразование фигуры F в
- 9. Центральная симметрияЕсли преобразование симметрии относительно точки О
- 10. Симметрия точкиотносительно прямойОчевидно что точка, симметрична точке
- 11. Симметрия фигурыотносительно прямойПреобразование фигуры F в фигуру
- 12. Ось симметрии(начало)Если преобразование симметрии относительно прямой g
- 13. Ось симметрии(продолжение)Например, прямые, проходящие через точку пересечения
- 14. Ось симметрии(продолжение)Преобразование симметрии относительно прямой является движениемА`АВВ`ОУХ
- 15. ПоворотПоворотом плоскости около данной точки называется такое
- 16. Параллельный перенос иего свойства1. При параллельном переносе
- 17. Параллельный перенос иего свойства2. При параллельном переносе прямая переходит в параллельную прямую (или в себя).(продолжение)АА`В`ОВВ
- 18. Параллельный перенос иего свойства(продолжение)3. Каковы бы ни
- 19. Равенство фигурДве фигуры называются равными, если они
- 20. Скачать презентанцию
Преобразование фигур Если каждую точку данной фигуры сместить каким-нибудь образом, то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной.
Слайды и текст этой презентации
Слайд 3Движение
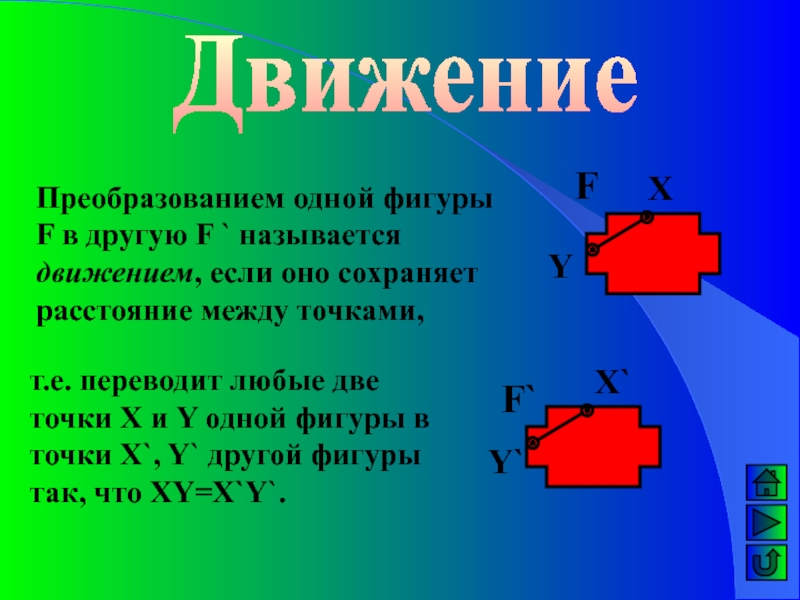
Преобразованием одной фигуры F в другую F ` называется движением,
если оно сохраняет расстояние между точками,
F`
F
Y`
Y
X
X`
т.е. переводит любые две точки
X и Y одной фигуры в точки X`, Y` другой фигуры так, что XY=X`Y`.
Слайд 4Свойства движения
Два движения, выполненные последовательно, дают снова движение.
F
F `; F ` F ``;
F F ``.F
F`
F``
Х
Х`
Х``
Слайд 5Свойства движения
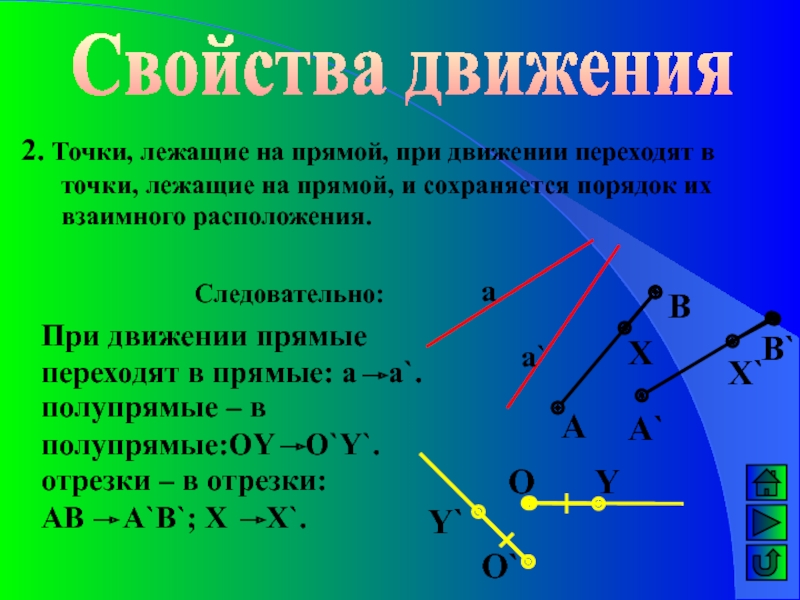
2. Точки, лежащие на прямой, при движении переходят в
точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
Следовательно:
При
движении прямые переходят в прямые: а а`. А
А`
B
B`
X
X`
O
O`
Y
Y`
a`
а
полупрямые – в полупрямые:OY O`Y`.
отрезки – в отрезки: АВ А`B`; Х Х`.
Слайд 7Симметрия
относительно точки
Пусть О – фиксированная точка
и Х –произвольная точка
плоскости
Отложим на продолжении отрезка ОХ за точку О отрезок ОX`,
равный ОХ.Точка X` называется симметричной точке Х относительно точки О. Точка, симметричная точке О, есть сама точка О. Очевидно, что точка, симметричная точке Х`, есть точка Х.
Х
Х`
О
Слайд 8Симметрия фигуры
относительно точки
Преобразование фигуры F в фигуру F`, при
котором каждая точка Х переходит в точку Х`, симметричную относительно
данной точки О, называетсяF
F`
X
X`
О
преобразованием симметрии относительно точки О. При этом фигуры F и F` называются симметричными относительно точки О.
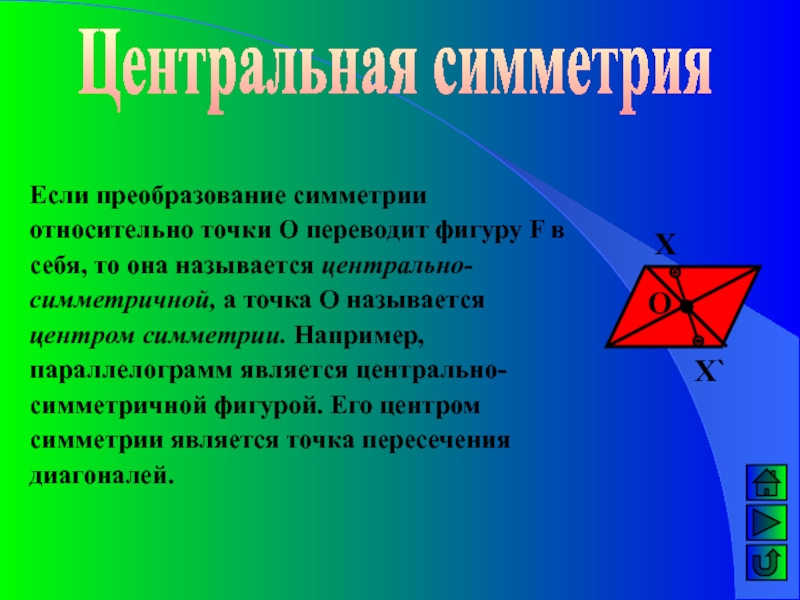
Слайд 9Центральная симметрия
Если преобразование симметрии относительно точки О переводит фигуру F
в себя, то она называется центрально-симметричной, а точка О называется
центром симметрии. Например, параллелограмм является центрально-симметричной фигурой. Его центром симметрии является точка пересечения диагоналей.Х
Х`
О
Слайд 10Симметрия точки
относительно прямой
Очевидно что точка, симметрична точке Х`, есть точка
Х.
Пусть g – фиксированная прямая.
Возьмем произвольную точку Х и опустим перпендикуляр АХ на прямую g.
На продолжении перпендикуляра за точку А отложим отрезок АХ`, равные отрезку АХ.
Точка Х `называется симметричной точке Х относительно прямой g.
Если точка Х лежит на прямой g, то симметричная ей точка есть сама точка Х.
Х
Х`
g
A
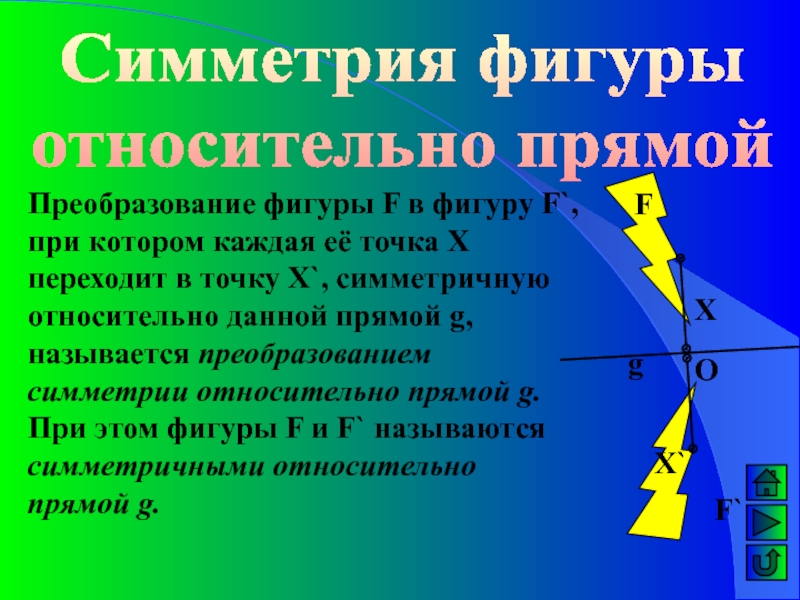
Слайд 11Симметрия фигуры
относительно прямой
Преобразование фигуры F в фигуру F`, при котором
каждая её точка Х переходит в точку Х`, симметричную относительно
данной прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F` называются симметричными относительно прямой g.g
X
X`
F
F`
О
Слайд 12Ось симметрии
(начало)
Если преобразование симметрии относительно прямой g переводит фигуру F
в себя, то эта фигура называется симметричной относительно прямой g,
а прямая g называется осью симметрии фигуры.Х
Х`
Слайд 13Ось симметрии
(продолжение)
Например, прямые, проходящие через точку пересечения диагоналей прямоугольника параллельно
его сторонам, являются осями симметрии прямоугольника. Прямые,на которых лежат диагонали
ромба,являются его осями симметрии.Х
Х`
Слайд 14Ось симметрии
(продолжение)
Преобразование симметрии относительно прямой является движением
А`
А
В
В`
О
У
Х
Слайд 15Поворот
Поворотом плоскости около данной точки называется такое движение, при котором
каждый луч, исходящий из этой точки, поворачивается на один и
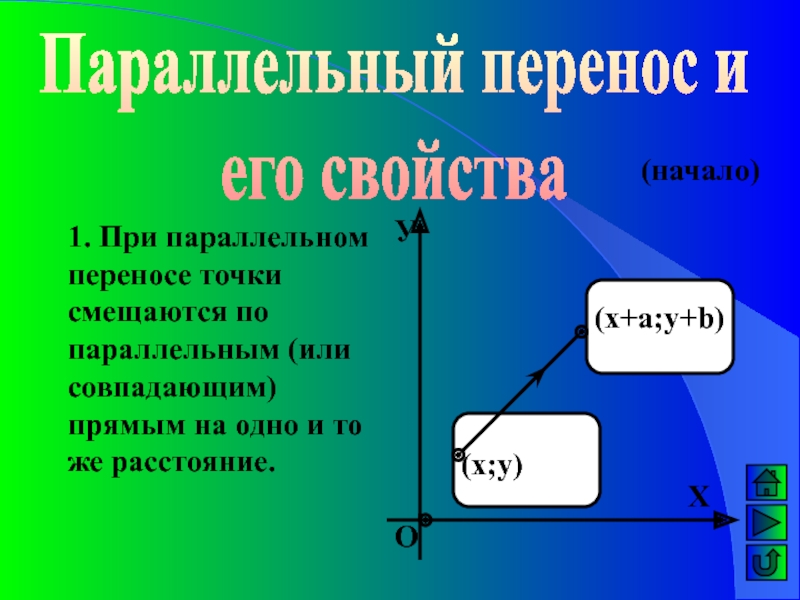
тот же угол в одном и том же направлении.
Слайд 16Параллельный перенос и
его свойства
1. При параллельном переносе точки смещаются по
параллельным (или совпадающим) прямым на одно и то же расстояние.
(х;у)
(х+а;у+b)
У
Х
О
(начало)
Слайд 17Параллельный перенос и
его свойства
2. При параллельном переносе прямая переходит в
параллельную прямую (или в себя).
(продолжение)
А
А`
В`
О
В
В
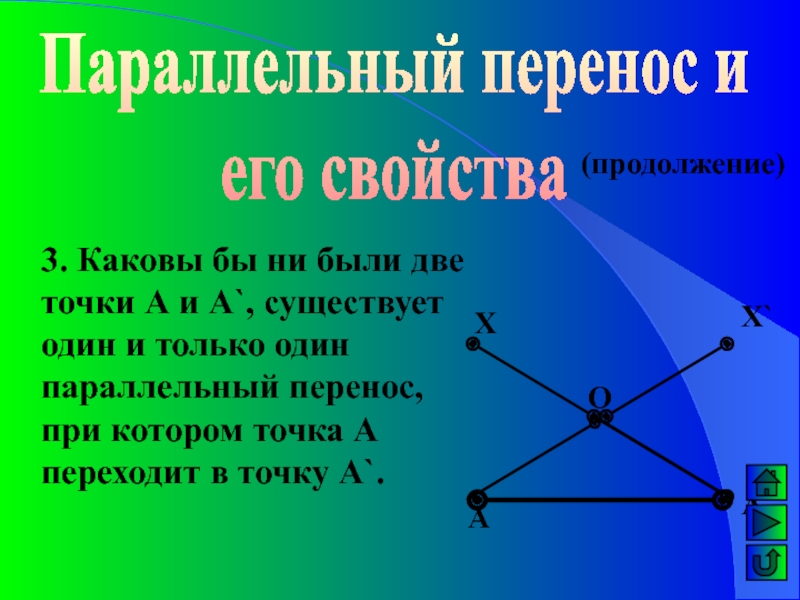
Слайд 18Параллельный перенос и
его свойства
(продолжение)
3. Каковы бы ни были две точки
А и А`, существует один и только один параллельный перенос,
при котором точка А переходит в точку A`.Х
Х`
А
А`
О
Слайд 19Равенство фигур
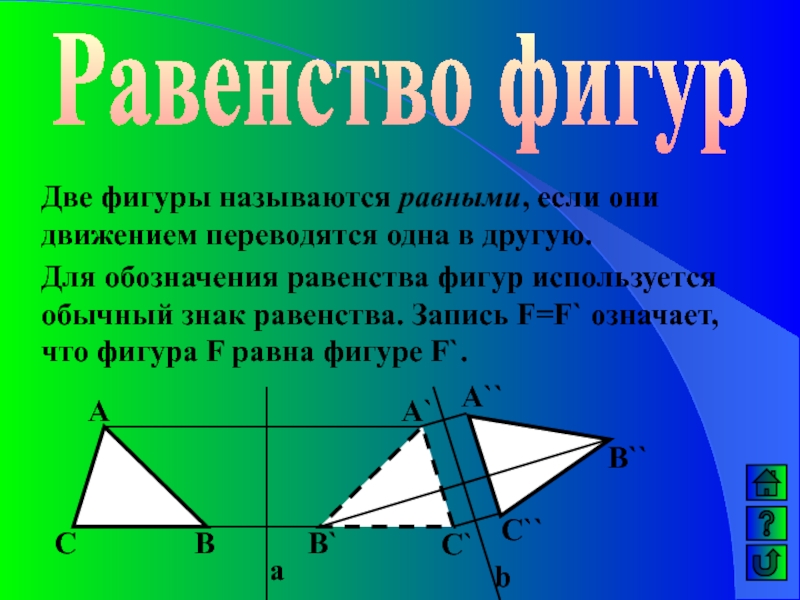
Две фигуры называются равными, если они движением переводятся одна
в другую.
Для обозначения равенства фигур используется обычный знак равенства. Запись
F=F` означает,что фигура F равна фигуре F`.А
А`
А``
В
В``
В`
С`
С``
С
a
b
