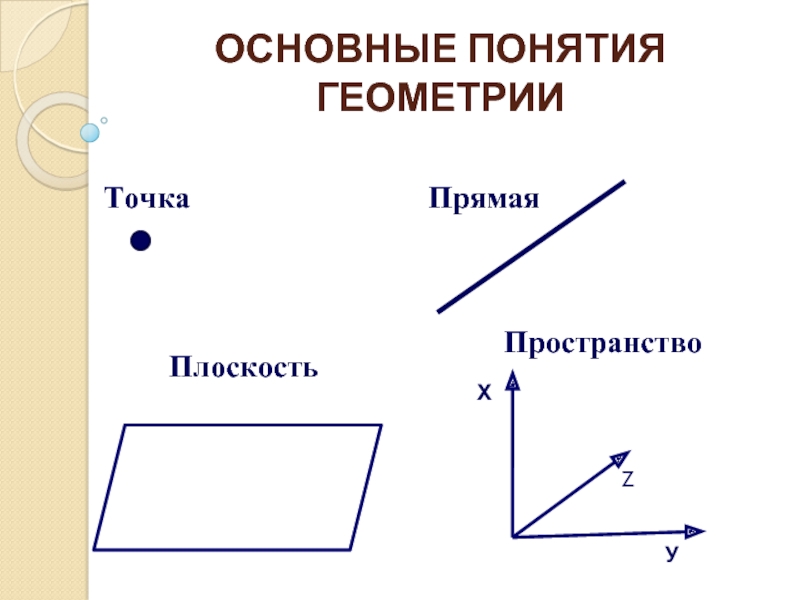
точки, прямой, плоскости и пространство друг от друга
Размеренность точки
– нулевая (ни в чем не измеряется).Размеренность прямой – единичная (измеряется в длине).
Размеренность плоскости – двойная (измеряется в длине и ширине).
Размеренность пространства – тройная (измеряется в длине, ширине и высоте).