Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема о вписанном угле
Содержание
- 1. Теорема о вписанном угле
- 2. МКЕNДано: ◡МКЕ в два раза меньше ◡MNE.Найти:
- 3. АКЕРОДано: ◡АКЕ на 140° меньше ◡АРЕ.Найти: ◡АРЕ.х(
- 4. 3) Дано: ◡АВ : ◡ВС : ◡АС=2:3:4 Найти: ∠АОВ, ∠ВОС, ∠АОС.ОАВС2х3х4х360°:9=40°Ответ: ◡АВ=80°, ◡ВС=120°, ◡АС=160°.
- 5. ОВАС50°40°DНайдите: ◡АDС, ∠АВС.25°20°Ответ: ◡АDС=90°∠АВС=45°
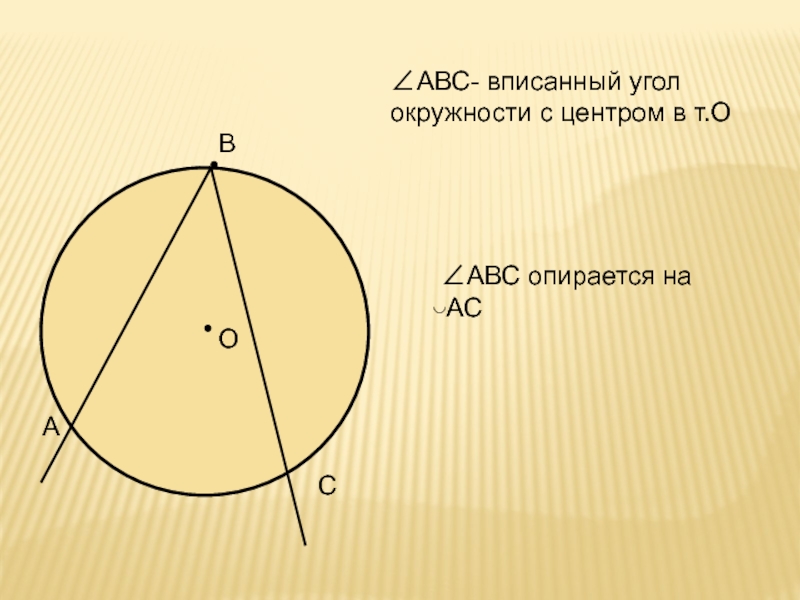
- 6. ОВАС ∠АВС- вписанный угол окружности с центром в т.О ∠АВС опирается на ◡АС
- 7. 1.2.3.4.ООООАВСЕНазовите вписанный угол.
- 8. Теорема: «Вписанный угол измеряется половиной
- 9. Луч ВО совпадает с одной из сторон
- 10. Доказательство:Проведем радиус ОА. ∆АОВ- равнобедренный ОА=ОВ, значит
- 11. ОАВСDДоказательство:Луч ОВ делит ◡АС=◡АD+◡CDПо доказанному ∠АВD=◡AD : 2 ∠CBD=◡CD : 2+∠ABD+∠CBD=(◡AD+◡CD):2 или∠АВС=◡АС : 2
- 12. ОАВСDПо доказанному∠ABD = ◡AD : 2∠CBD = ◡CD : 2-∠ABD-∠CBD=(◡AD-◡CD):2 или∠АВС = ◡АС : 2
- 13. ОАВС1. ◡ВС=48°, найди ∠ВАС ОМNК2. ∠МNК=20°, найди ◡МКОАСN3. ∠АОС=86°, найди ∠АNCОFENC4. ∠FCN=47°, найди ∠FEN
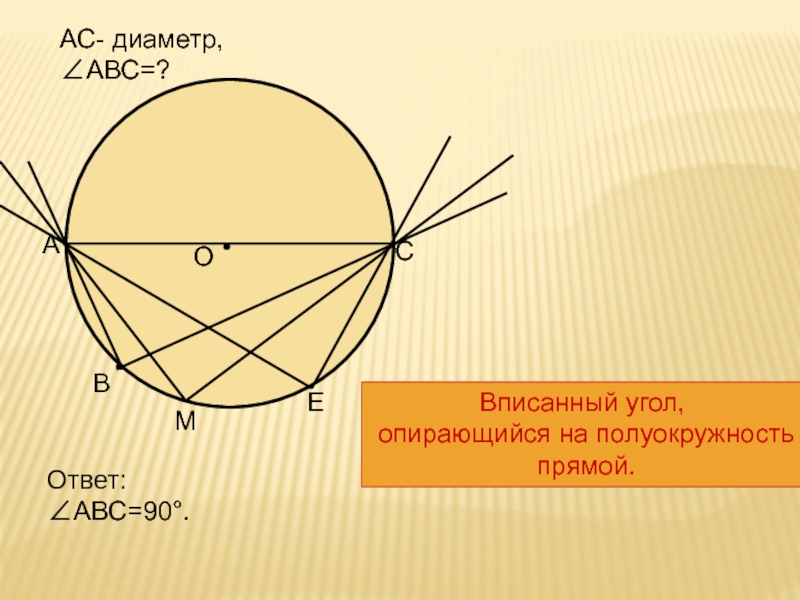
- 14. ОВАСАС- диаметр, ∠АВС=?Ответ: ∠АВС=90°.МЕВписанный угол, опирающийся на полуокружность прямой.
- 15. Решение задач:№656,№658.
- 16. ОВАСОАВС№656
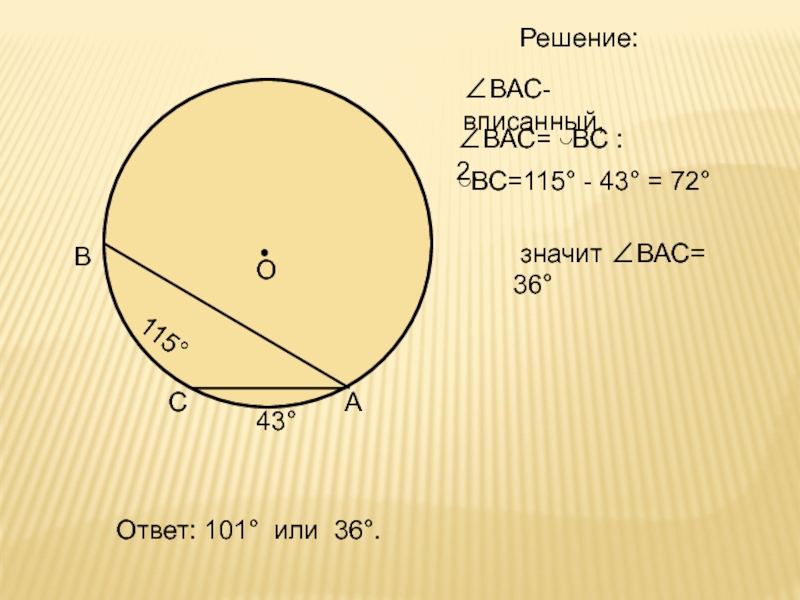
- 17. ОВАСРешение:∠ВАС- вписанный,∠ВАС= ◡ВС : 2.115°43°◡ВС=360°-(115°+4°)=202°, значит ∠ВАС=101°
- 18. ОВАСРешение:∠ВАС- вписанный,∠ВАС= ◡ВС : 2.115°43°◡ВС=115° - 43° = 72° значит ∠ВАС= 36°Ответ: 101° или 36°.
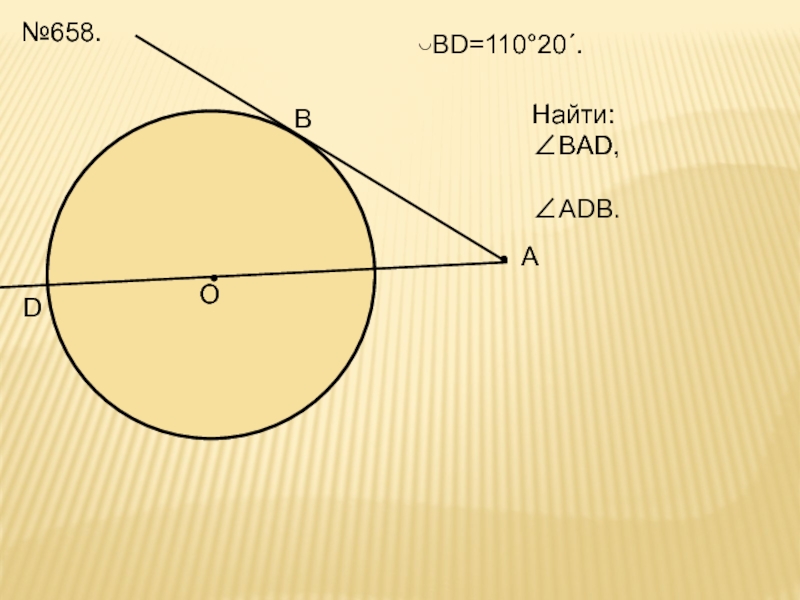
- 19. №658.
- 20. ОВАD◡BD=110°20´.Найти: ∠ВAD, ∠ADB.№658.
- 21. ОВАD◡BD=110°20´.Найти: ∠ВAD,
- 22. Домашнее задание: п.71, вопросы 11-13,
- 23. Скачать презентанцию
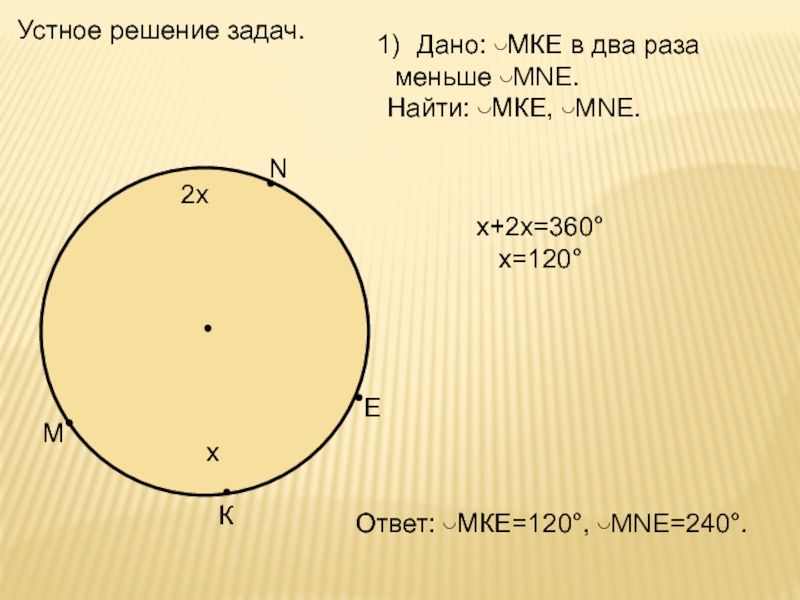
МКЕNДано: ◡МКЕ в два раза меньше ◡MNE.Найти: ◡МКЕ, ◡MNE. х2х х+2х=360° х=120°Ответ: ◡МКЕ=120°, ◡MNE=240°.Устное решение задач.
Слайды и текст этой презентации
Слайд 3А
К
Е
Р
О
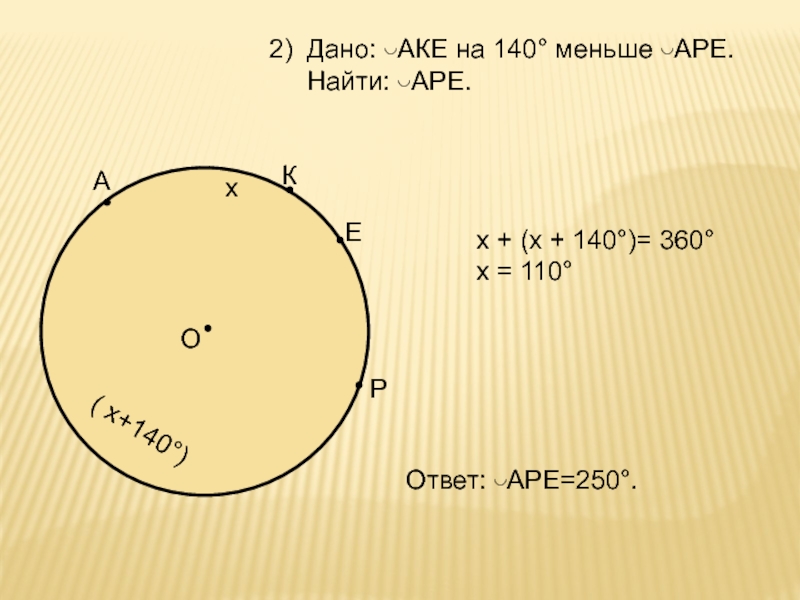
Дано: ◡АКЕ на 140° меньше ◡АРЕ.
Найти: ◡АРЕ.
х
( х+140°)
х +
(х + 140°)= 360°
х = 110°
Ответ: ◡АРЕ=250°.
2)
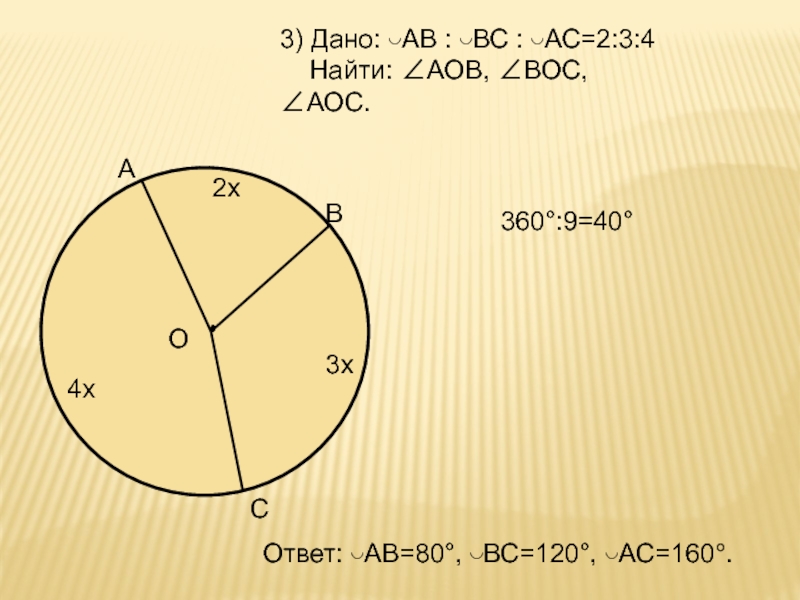
Слайд 43) Дано: ◡АВ : ◡ВС : ◡АС=2:3:4
Найти: ∠АОВ,
∠ВОС, ∠АОС.
О
А
В
С
2х
3х
4х
360°:9=40°
Ответ: ◡АВ=80°, ◡ВС=120°, ◡АС=160°.
Слайд 8Теорема: «Вписанный угол измеряется половиной
дуги, на которую он опирается».
О
А
В
С
Дано: ∠АВС-
вписанный,опирающийся на ◡АС;
О- центр окружности.
Доказать: ∠АВС= ◡АС : 2.
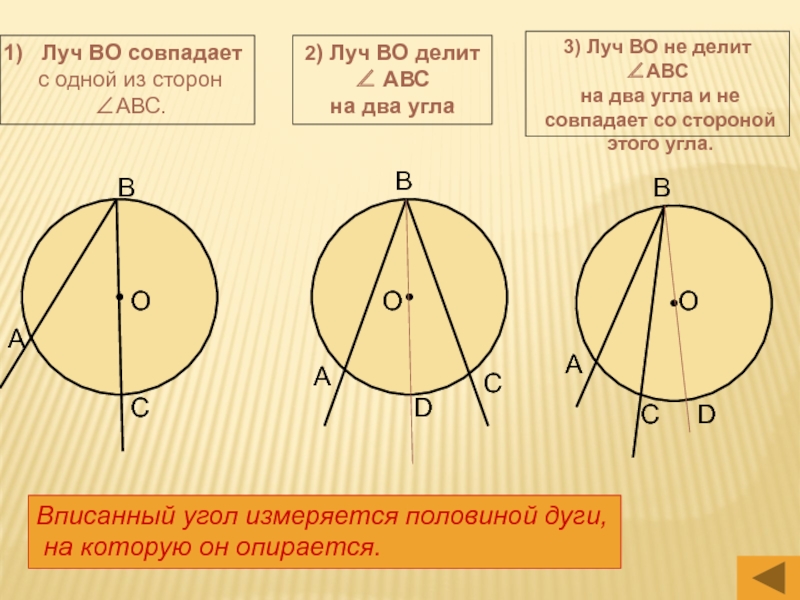
Слайд 9Луч ВО совпадает
с одной из сторон
∠АВС.
2) Луч
ВО делит
∠ АВС
на два угла
3) Луч ВО не делит
∠АВСна два угла и не
совпадает со стороной
этого угла.
О
О
О
В
В
В
А
С
А
С
А
С
D
D
Вписанный угол измеряется половиной дуги,
на которую он опирается.
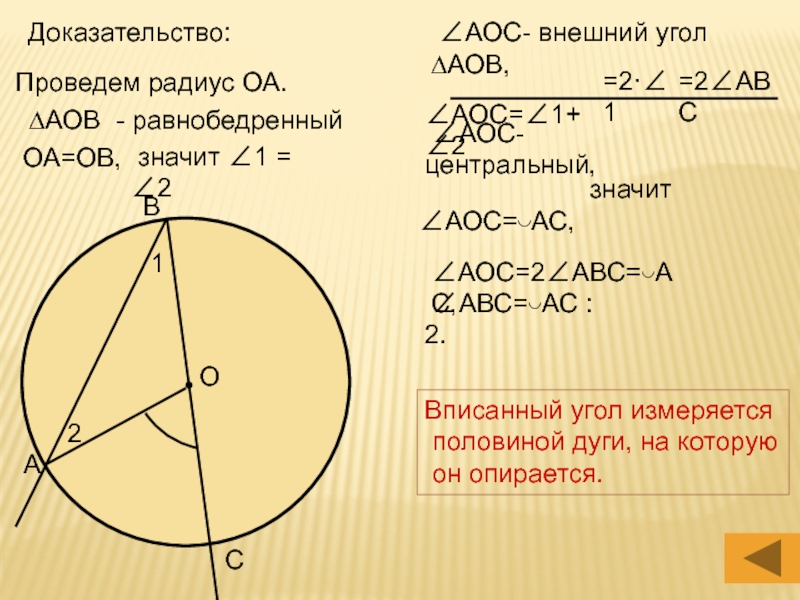
Слайд 10Доказательство:
Проведем радиус ОА.
∆АОВ
- равнобедренный
ОА=ОВ,
значит ∠1 = ∠2
О
В
А
С
∠АОС- внешний угол ∆АОВ,
∠АОС=∠1+∠2
=2·∠1
=2∠АВС
∠АОС- центральный,
∠АОС=◡АС,
значит
∠АОС=2∠АВС=◡АС,
∠АВС=◡АС : 2.Вписанный угол измеряется
половиной дуги, на которую
он опирается.
1
2
Слайд 11О
А
В
С
D
Доказательство:
Луч ОВ делит ◡АС=◡АD+◡CD
По доказанному
∠АВD=◡AD : 2
∠CBD=◡CD :
2
+
∠ABD+∠CBD=(◡AD+◡CD):2
или
∠АВС=◡АС : 2
Слайд 13О
А
В
С
1. ◡ВС=48°, найди ∠ВАС
О
М
N
К
2. ∠МNК=20°, найди ◡МК
О
А
С
N
3. ∠АОС=86°, найди
∠АNC
О
F
E
N
C
4. ∠FCN=47°, найди ∠FEN
Слайд 14О
В
А
С
АС- диаметр, ∠АВС=?
Ответ: ∠АВС=90°.
М
Е
Вписанный угол,
опирающийся на полуокружность
прямой.
Слайд 18О
В
А
С
Решение:
∠ВАС- вписанный,
∠ВАС= ◡ВС : 2.
115°
43°
◡ВС=115° - 43° = 72°
значит
∠ВАС= 36°
Ответ: 101° или 36°.
Слайд 21О
В
А
D
◡BD=110°20´.
Найти: ∠ВAD,
∠ADB.
∠DOB=110°20´,
∆DOB- равнобедренный,
1
2
∠ВDО=(180°-110°20´) : 2
∠АDВ=34°50´.
∆ВОА,
∠В=90°,
∠О=69°40´
∠ВАО=90° - 69°40´ = 20°20´.
Ответ: ∠ВАО=20°20´; ∠АDВ=34°50´.
№658.
